Arcan-Prüfkörper
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Arcan-Prüfkörper
Allgemeines
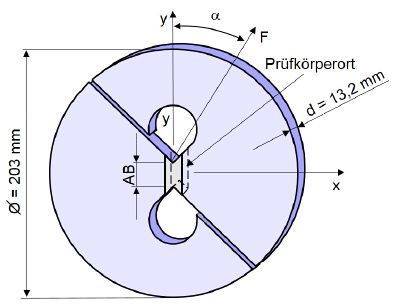
Mit dem Arcan-Prüfkörper können bruchmechanische Kennwerte bei Mode I, Mode II und Mixed Mode Belastung ermittelt werden. Der Bruchmechanikprüfkörper und die dazugehörige Arcan-Vorrichtung wurden nach ihrem Erfinder benannt [1]. Sie wurde mit dem Ziel entwickelt, eine gleichförmige ebene Spannung in dem Testbereich zu erhalten (siehe Bild 1).
Prüfkörperform
| Bild 1: | Arcan-Testvorrichtung und Prüfkörpergeometrie |
Der Prüfkörper wird mit einem einseitigen Anfangsriss versehen (z. B. V-Kerb). Erfolgt die Belastung in y-Richtung erhält man folgende Beanspruchungsmoden:
| = 0° | Mode I |
| = 45° | Mixed Mode |
| = 90° | Mode I |
Durch Veränderung des Winkels wird ein kombinierter Zug- und Scherspannungszustand im Testbereich erreicht. Ein Vorteil dieses Prüfkörpers ist die Wiederverwendbarkeit der Metallvorrichtung. Der Verbundwerkstoffprüfkörper wird an die Metallvorrichtung geklebt und kann nach dem Testen durch erhitzen des Prüfkörpers und der Vorrichtung über die Glasübergangstemperatur des Klebers abgelöst werden.
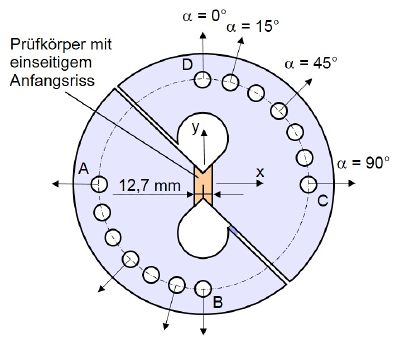
Jurf und Pipes [2] erweiterten den Nutzen der Vorrichtung durch den Austausch der charakteristischen V-gekerbten Arcan-Prüfkörper mit einem einseitig angerissenen Prüfkörper (siehe Bild 2).
| Bild 2: | Arcan-Bruchmechanikprüfkörper |
Durch Veränderung des Winkels von auf 90° können Werte für Modus II, Mixed-Mode und Modus I gesammelt werden (siehe Bruchmoden). Der gewählte Belastungswinkel wird durch Montierung der Vorrichtung mit zwei gegenüberliegenden Bohrungen erreicht.
Bestimmungsgleichung für Spannungsintensitätsfaktoren
Für einen gegebenen Winkel können die "Fernfeld"-Normal- und Scherspannung erhalten werden, wobei die Spannung als die aufgewendete Kraft F dividiert durch die Querschnittsfläche A des Verbundwerkstoffprüfkörpers definiert ist.
Basierend auf den Normal- und Scherspannungskomponenten können die Spannungsintensitätsfaktoren KI (Modus I) und KII (Modus II) bestimmt werden:
wobei a die Risslänge und c die Abmessung des Prüfkörpers entlang des Risses ist. Die Korrekturfaktoren fI und fII sind in [2] für endliche Risslängen-zu-Prüfkörperlängen-Verhältnisse angegeben:
Anwendungsbeispiel für Faserverbundwerkstoffe
Von Jurf und Pipes [2] wurde für ein Epoxidharz/C-Faserverbund bruchmechanische Kennwerte bestimmt. Die Ergebnisse wurden in tabellarischer Form in [1] zusammengestellt.
| Prüfkörpernummer | (°) |
Fmax (kN) |
KI (MPam1/2) |
KII (MPam1/2) |
GI (N/mm) |
GII (N/mm) |
|---|---|---|---|---|---|---|
| 1 (Mode II) | 0 | 10,30 | 0 | 6,60 | 0 | 0,91 |
| 2 (Mode II) | 0 | 10,90 | 0 | 6,80 | 0 | 0,98 |
| 3 (Mixed Mode) | 45 | 0,97 | 0,99 | 0,45 | 0,084 | 0,004 |
| 4 (Mixed Mode) | 45 | 1,30 | 1,31 | 0,59 | 0,15 | 0,007 |
| 5 (Mode I) | 90 | 0,70 | 1,07 | 0 | 0,10 | 0 |
| 6 (Mode I) | 90 | 0,68 | 1,01 | 0 | 0,09 | 0 |
Eine umfassende Literaturanalyse zu bruchmechanischen Kennwerten für Faserverstärkte Verbundwerkstoffe wurde von Lach in [3] zusammengestellt.
Literaturhinweise
| [1] | Carlsson, L. A., Pipes, R. B.: Hochleistungsfaserverbundwerkstoffe. B. G. Teubner, Stuttgart (1989) (ISBN 978-3-5190-3250-2) |
| [2] | Jurf, R. A. und Pipes, R. B.: Interlaminar Fracture of Composite Materials. Journal of Composite Materials 16 (1982) 386–394 |
| [3] | Lach, R., Grellmann, W.: Thermosets and High Performance Composites. In: Grellmann, W., Seidler, S.: Mechanical and Thermomechanical Properties of Polymers. Landolt-Börnstein. Volume VIII/6A3, Springer Verlag, Berlin (2014) S. 423–492, (ISBN 978-3-642-55165-9; siehe AMK-Büchersammlung unter A 16) |







![{\displaystyle f_{II}\left(a/c\right)={\frac {1,122-0,561\left(a/c\right)+0,085\left(a/c\right)^{2}+0,180\left(a/c\right)^{3}}{\left[1-\left(a/c\right)\right]^{1/2}}}}](https://de.wikipedia.org/api/rest_v1/media/math/render/svg/b1bbb0ed557f0bccb78f3fe9ae39dc9ceab8d90f)