Biegeversuch Einflüsse
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Biegeversuch Einflüsse
Elastische Biegetheorie
Die elastische Linie für große Durchbiegungen w wird mit der allgemeinen Differentialgleichung der elastischen Biegelinie des deformierten Biegeprüfkörpers beschrieben (Theorie 2. Ordnung), die unter ingenieurtechnischen Gesichtspunkten kompliziert handhabbar ist und nur auf numerischen Wege lösbar ist (Gl. 1), da die
| (1) |
Randbedingungen wie auch die Gleichung selbst von der Neigung der Biegelinie w' abhängen. Aus diesem Grund wird in den einschlägigen Normen [2, 3] der Biegeprüfung an Kunststoffen auf den Einfluss der Prüfkörperneigung verzichtet und die vereinfachte Theorie 1. Ordnung für die Biegedifferentialgleichung (Gl. 2) verwendet.
| (2) |
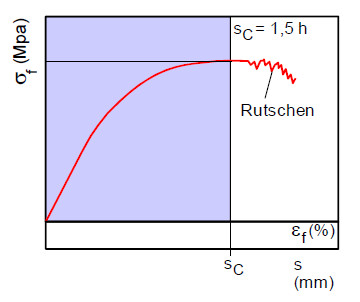
Diese vereinfachte Form der Differentialgleichung der Biegung ist aber eigentlich nur für kleine Deformationen, d. h. die Durchbiegung ist sehr viel kleiner als die geometrischen Abmessungen (Dicke). Aufgrund der dann nur geringfügigen Neigungen an den Auflagern des Prüfkörpers können die entsprechenden Lösungen zur Berechnung der Kennwerte des Biegeversuchs genutzt werden. Da bei großen Durchbiegungen die Spannungs-Dehnungs-Kurve durch unvermeidbare Rutscheffekte beeinflusst wird (Bild 1) wurde in der ursprünglichen Fassung der DIN EN ISO 178 ein Grenzwert von 3,5 % Randfaserdehnung festgelegt, bis zu dem Biegeversuche normgerecht durchgeführt werden können. Dieser Wert wird heute als konventionelle Durchbiegung sC bezeichnet und beträgt bei einem 4 mm dicken Prüfkörper dann 6 mm [1]. In der aktuellen Fassung der Norm für die Dreipunktbiegeprüfung an Kunststoffen [2] werden für die Durchbiegung sogar Werte > 9 mm zugelassen, für die die Biegetheorie 1. Ordnung eigentlich keine gültigen Resultate liefern kann.
| Bild 1: | Rutschen des Prüfkörpers auf den Widerlagern bei großen Durchbiegungen |
Mit den bekannten Gleichungen der elastischen Biegetheorie werden natürlich die Fehler, die sich durch die HERTZ´sche Pressung an den Widerlagern, das Abrollen des Prüfkörpers auf dem Widerlagerradius oder die damit verbundene Auflagerabstandsverkürzung ergeben, vernachlässigt. Man kann hierbei zwischen Einflussfaktoren unterscheiden, die man im Kraftsignal eigentlich berücksichtigen müsste und die sich in der berechneten Biegespannung niederschlagen, sowie Messfehlern, die in die Durchbiegung und demzufolge auch in die Randfaserdehnung eingehen. Im Bild 2 werden diese Einflussgrößen veranschaulicht.
Einflüsse auf die Berechnung der Biegespannung
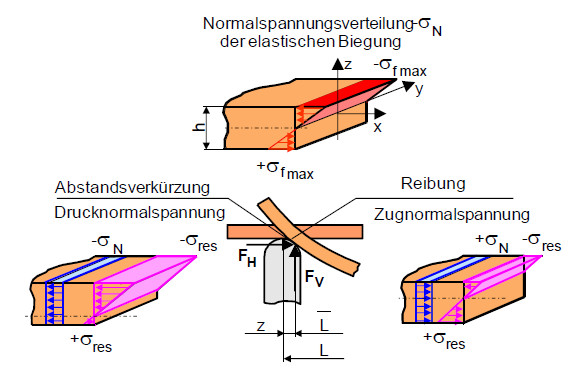
| Bild 2: | Einfluss von Reibung und Verkürzung des Widerlagerabstandes auf die Spannung |
Aus Bild 2 ist zu erkennen, dass die sich theoretisch einstellende symmetrische Spannungsverteilung bezüglich des Prüfkörperquerschnittes mit zunehmendem Radius des Widerlagers und größeren Durchbiegungen stärker durch die Normalspannungen (Zug und Druck) beeinflusst wird. Geometrisch lässt sich diese Einflussgröße durch den Wert z ausdrücken. Die resultierende Spannung σres kann aus der Reibung an den Widerlagern entstehen oder durch die Abstandsverkürzung mit der Horizontalkraft FH verursacht werden. Die Reibungskraft hängt dabei natürlich von der Paarung der Werkstoffe des Widerlagers und des untersuchten Werkstoffes ab und muss experimentell bestimmt werden. In beiden Fällen entsteht somit ein asymmetrisches Spannungsprofil, wobei sich diese Effekte überlagern und eine nicht exakt vorherbestimmbare Verschiebung der neutralen Faser verursachen. Neben diesen Einflussfaktoren kann die HERTZ´sche Pressung unter dem Widerlager und dem Belastungsstempel eine Druckspannung hervorrufen, die jedoch sehr schnell zur Mitte des Prüfkörpers hin abfällt und deshalb nicht weiter betrachtet wird.
Einflüsse auf die Berechnung der Randfaserdehnung
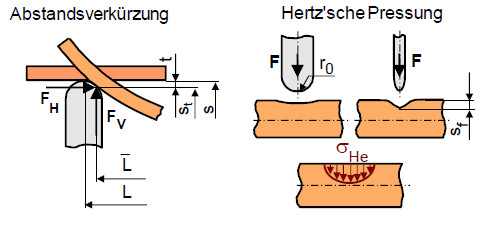
Durch die Nutzung von runden Widerlagern wird aufgrund des behinderten Abrollens des Prüfkörpers auf dem Lager gleichzeitig ein Differenzweg t entstehen, der von der eingeprägten Durchbiegung s bzw. w abhängt (Bild 3).
| Bild 3: | Einfluss von lokaler Pressung und Widerlagerabstandsverkürzung auf die Dehnung |
Unter der Voraussetzung einer Traversenwegmessung sind dann die ermittelte Durchbiegung und die resultierende Randfaserdehnung geringer, wodurch größere Kräfte benötigt werden. In das gemessene Signal können infolge der Radiengestaltung dann auch Fehlwege wf eingehen, die indirekt von der HERTZ´sche Pressung abhängig sind, und ebenfalls eine kleinere Durchbiegung hervorrufen. Eine näherungsweise Berücksichtigung der aufgeführten Einflussfaktoren auf die berechnete Biegespannung ist nachfolgend am Beispiel der Dreipunkt-Biegung dargestellt.
Berechnung der Biegespannung im Dreipunktbiegeversuch
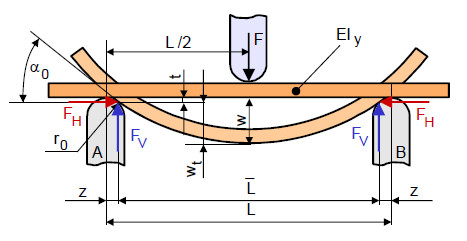
Wie dem Bild 4 zu entnehmen ist, hängt die entstehende Horizontalkraft FH von der Neigung am Widerlager ab und führt zu einer Drucknormalspannung bezüglich des Querschnittes und einer korrigierten Biegespannung (Gl. 3), wobei Wb das Widerstandsmoment ist. Neben der reinen Normalspannung bewirkt FH jedoch auch ein zusätzliches Biegemoment, welches von der sich einstellenden Durchbiegung abhängig ist. Damit korrigiert sich die resultierende Biegespannung zu der Gleichung (3).
| Bild 4: | Berücksichtigung des Einflusses der Auflagerabstandsverkürzung |
Die Verringerung des Auflagerabstandes wird im Biegemoment über den Korrekturfaktor z erfasst. Die diesbezüglich korrigierte Biegespannung hängt erwartungsgemäß von der sich einstellenden Durchbiegung w und dem Widerlagerradius r0 ab. Die Berücksichtigung aller dieser verschiedenen Einflussfaktoren führt in der Konsequenz zur Gleichung (3):
| (3) |
Bei der Durchbiegung kann der entstehende Fehler t relativ leicht über den bekannten Wert von z und die Auflagergeometrie korrigiert werden, wodurch sich die nachfolgende Korrekturgleichung ergibt. Eine analoge Vorgehensweise ist bei der Vierpunktbiegung möglich, wobei sich dort jedoch kompliziertere Korrekturgleichungen ergeben.
| (4) |
Die Korrekturgleichungen, die in der Norm DIN EN ISO 14125 [3] angegeben werden, weichen etwas von den oben angegebenen Lösungen ab, ergeben allerdings nahezu identische Ergebnisse, wobei hier für die Durchbiegung s anstatt w verwendet wird. Für die Berücksichtigung der Reibung muss der Reibungskoeffizient μ experimentell bestimmt werden (Gl. 6). Die korrigierte Biegespannung im Dreipunktbiegeversuch ergibt sich hier nach Gl. (5):
| (5) |
| (6) |
Die korrigierte Durchbiegung berechnet sich nach Gleichung (7):
| (7) |
Literaturhinweise
| [1] | Bierögel, C.: Biegeversuch an Kunststoffen. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 147–158 (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18)) |
| [2] | DIN EN ISO 178 (2019-08): Kunststoffe – Bestimmung der Biegeeigenschaften |
| [3] | DIN EN ISO 14125 (2011-05): Faserverstärkte Kunststoffe – Bestimmung der Biegeeigenschaften |
![{\displaystyle {\frac {w^{\prime \prime }(x)}{\left[1+w^{\prime 2}(x)\right]^{\frac {3}{2}}}}=-{\frac {M(x)}{EI}}}](https://de.wikipedia.org/api/rest_v1/media/math/render/svg/c9b145603a3f88729580d606d9f4525d81d4bda0)

![{\displaystyle \sigma _{f}={\frac {3FL}{2bh^{2}}}\left[1+{\frac {6w^{2}}{L^{2}}}-{\frac {hw}{L^{2}}}-{\frac {2r_{0}}{L}}sin\ arctan\left({\frac {3w}{L}}\right)\right]}](https://de.wikipedia.org/api/rest_v1/media/math/render/svg/84a611abd21a9e022554bdd266e3f0ab4ecb41b6)
![{\displaystyle \epsilon _{f}={\frac {{\frac {6hw}{L^{3}}}\left[L-2r_{0}sin\ arctan{\frac {3w}{L}}\right]^{3}-6hr_{0}\left[1-cos\ arctan{\frac {3w}{L}}\right]}{\left[L-2r_{0}sin\ arctan{\frac {3w}{L}}\right]^{2}}}\ 100\ \%}](https://de.wikipedia.org/api/rest_v1/media/math/render/svg/3d90256d9df12194089371d44adfebdb723be37f)
![{\displaystyle \sigma _{f}={\frac {3FL}{2bh^{2}}}\left[1+{\frac {6s^{2}}{L^{2}}}-{\frac {hws}{L^{2}}}\right]}](https://de.wikipedia.org/api/rest_v1/media/math/render/svg/dda264fa86e118d9a77d3b9005539480d6ffe13f)
![{\displaystyle \sigma _{f}={\frac {3FL}{2bh^{2}}}\left[1+{\frac {6s^{2}}{L^{2}}}-{\frac {hws}{L^{2}}}-{\frac {\mu }{L}}(2s-h)\right]}](https://de.wikipedia.org/api/rest_v1/media/math/render/svg/94241bb78ec0c1849bde33d98d2a0fb991b89eb8)
![{\displaystyle \epsilon _{f}={\frac {h}{L}}\left[{\frac {6s}{L}}-24,37\left({\frac {s}{L}}\right)^{3}+62,17\left({\frac {s}{L}}\right)^{5}\right]\ 100\ \%}](https://de.wikipedia.org/api/rest_v1/media/math/render/svg/dd2099bf9c610faf079319c8b6cecf5a77330413)