Bruchentstehung
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Bruchentstehung
Die Verformungsenergie für die Bruchentstehung
Um die Vorgänge bei der Bruchentstehung zu erläutern, ist eine vergleichende Betrachtung zwischen einem unbelasteten Zugprüfkörper und einem beanspruchten Zugprüfkörper ohne und mit Riss zweckmäßig.
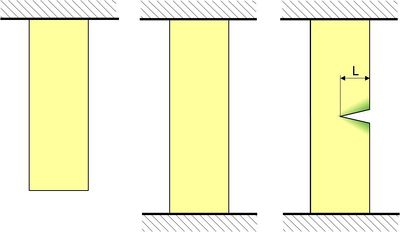
| Bild 1: | Dehnung und Rissbildung bei einem fest eingespannten Zugprüfkörper. Beim Dehnen wird Energie im Material gespeichert. Ein Riss führt nun in seiner Umgebung (grüne Bereiche) dazu, dass sich das Material entspannt und die gespeicherte Energie freisetzt, so dass der Riss sich weiter ausbreiten kann. |
Im unbelasteten Zustand gibt es natürlich keinerlei Deformationsenergie. Setzen wir den Prüfkörper nun einer Zugbelastung σ aus, dann wird pro Volumeneinheit die Energie σ2/2E gespeichert, und solange beide Enden fest eingespannt sind, kann diese mechanische Energie das Material nicht verlassen. Sofern keine Defekte vorliegen, verteilt sich die Energie annähernd homogen über das Probenvolumen. Nehmen wir nun an, dass auf einer Seite des Prüfkörpers ein Riss der Länge L vorhanden ist. Auf beiden Seiten dieses etwas auseinander klaffenden Risses kann sich das Material entspannen (grüne Bereiche im Bild), da keine Lastspannung übertragen werden kann. Beim Entspannen wird der größte Teil der gespeicherten Verformungsenergie frei, die dann für den Bruchmechanismus zur Verfügung steht, so dass sich der Riss ausbreiten kann.
Die freie Oberflächenenergie
Die Entstehung frischer Bruchflächen erfordert eine Energie, deren Betrag mindestens so groß sein muss wie die freie Oberflächenenergie γ. Tatsächlich kann der Energiebedarf auch weit höher liegen. Als Bruchenergie W wird die gesamte Energie definiert, die für eine neue Oberfläche beim Reißen über eine Längeneinheit erforderlich ist. Die Bruchenergie beträgt für einen Riss der Länge L mit seinen zwei Bruchflächen also 2 WL, d. h. sie steigt proportional zur Risslänge L an.
Im Gegensatz zum linearen Anstieg der Bruchenergie erhöht sich die freigesetzte Verformungsenergie meist proportional zu L2. Diesen quadratischen Anstieg spiegeln die grün markierten dreieckigen Flächen im Bild 1 wider. Trägt man die Verformungsenergie als Funktion der Risslänge auf, so ergibt sich normalerweise als Kurve eine Parabel. Anhand der Kurve für Bruch- und Verformungsenergie lassen sich der Energiebedarf und die Energiefreisetzung (siehe Energiefreisetzungsrate) beim Reißen vergleichen (siehe Bild 2).
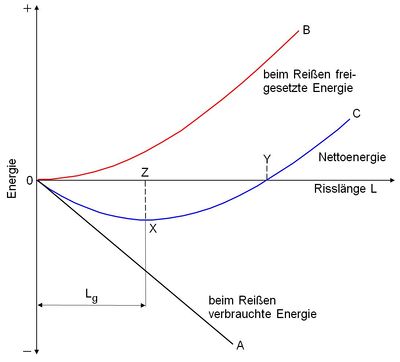
| Bild 2: | Energiebilanz bei der Rissausbreitung. Sobald ein Riss eine kritische Länge Lg erreicht, wird durch weiteres Reißen mehr Energie freigesetzt als verbraucht – die Nettoenergie nimmt zu. |
Die Energie für die Rissausbreitung
Bis zum Punkt X der Kurve für die Nettoenergie wird beim Reißen insgesamt Energie verbraucht. Oberhalb dieses Punktes setzt das System dagegen Energie frei, und der Riss breitet sich von selbst weiter aus. Risse, die kürzer sind als die kritische Griffith-Länge Lg, sind aus energetischen Gründen stabil. Sobald die kritische Länge überschritten wird, sind Risse instabil und breiten sich mit wachsender Länge immer schneller aus.
Griffiths Berechnungen für die kritische Länge Lg sind mathematisch kompliziert, aber sein Endresultat ist dann wieder ermutigend einfach:
Anhand der Formeln lässt sich Lg algebraisch ausdrücken:
Dabei bezeichnet W die Bruchenergie, die für einen Quadratmeter erforderlich ist (und in J/m2 gemessen wird); E ist der Elastizitätsmodul (in N/m2), σ die mittlere Zugfestigkeit (ohne Berücksichtigung von Spannungskonzentrationen) in der Umgebung des Risses (in N/m2) und Lg die kritische Länge (in m).
Wenn man nun W wieder mit der Oberflächenenergie γ eines Festkörpers gleichsetzt, lässt sich rechnerisch leicht zeigen, dass der Ansatz mit Kräften zum selben Ergebnis führt wie das Energieargument. Für einen Riss oder Defekt der Länge L ergeben sich rechnerisch in beiden Fällen die gleichen Auswirkungen. Griffith wies jedoch darauf hin, dass selbst bei sehr spröden Materialien wie Glas die Energie W, die für die Rissbildung aufgewandt werden muss, größer als die Oberflächenenergie γ ist. Reißen beinhaltet nämlich nicht nur, dass Atom- oder Molekülbindungen getrennt werden, sondern außerdem wird auch die Materialstruktur gestört bzw. geschädigt.
Literaturhinweis
- Gordon, J. E.: Strukturen unter Stress. Mechanische Belastbarkeit in Natur und Technik. Aus dem Amerikanischen übersetzt von Axel Bewersdorf. Spektrum der Wissenschaft, In: Spektrum-Bibliothek Bd. 21, Heidelberg (1987) S. 90–92 (ISBN 978-3-9225-0894-6) (siehe AMK-Büchersammlung unter L 33)