DCB-Prüfkörper
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
DCB-Prüfkörper
Die angelsächsische Abkürzung DCB steht für "Double-Cantilever Beam".
Die Beanspruchung des DCB-Prüfkörpers kann entweder durch eine konstante Belastung (F = konst.) oder über eine konstante Verformung (v = konst.) mittels Keils oder Schrauben aufgebracht werden.
Prüfkörperformen
Von Blumenauer [1, 2] wird gefordert, dass über die Prüfkörperabmessung zu gewährleisten ist, dass die Größe der plastischen Zone (siehe auch effektive Risslänge) klein gegenüber der Risslänge und den Prüfkörperabmessungen ist.
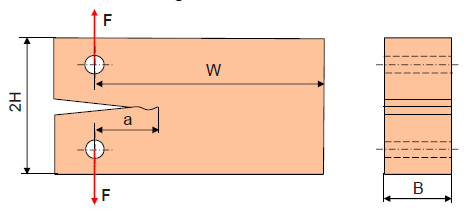
Versuchsdurchführung F = konst.
|
|
| Bild 1: | Schematische Darstellung des DCB-Prüfkörpers bei konstanter Belastung |
Bestimmungsgleichung [1, 2]
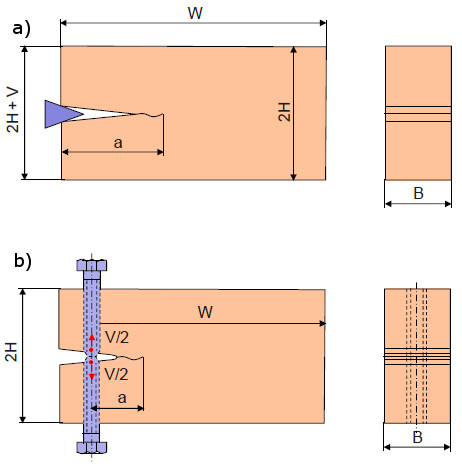
Versuchsdurchführung v = konst.
|
|
| Bild 2: | Schematische Darstellung von DCB-Prüfkörpern bei konstanter Verformung; Realisierung mit Keil (a) und mit Schrauben (b) |
Bestimmungsgleichung [1, 2]
mit
| KI | Bruchzähigkeit | |
| E | Elastizitätsmodul |
Weitere Prüfkörperform: TDCB-Prüfkörper (Tapered-Double-Cantilever Beam)-Prüfkörper
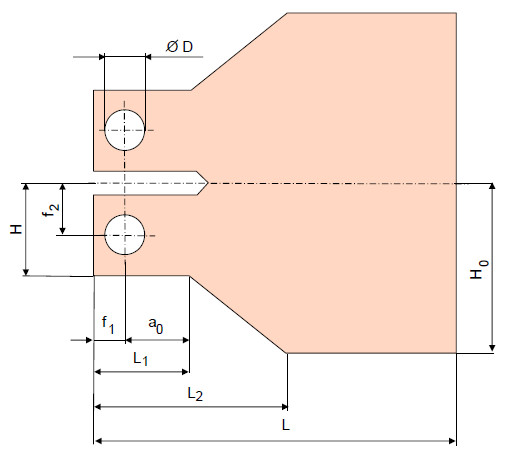
In der Literatur werden unterschiedliche Prüfkörperformen desselben Grundtyps beschrieben. Von Blumenauer wird in [1] ein derartiger Prüfkörpertyp angegeben.
|
|
| Bild 3: | Schematische Darstellung des TDCB-Prüfkörpers nach [1] |
Bestimmungsgleichung
Belastung durch Zugkraft F:
Belastung durch Kerbaufweitung V:
für 0,8 < (a/H) < 2,4
Eine weitere Form eines TDCB-Prüfkörpers wird unter Prüfkörper für bruchmechanische Prüfungen aufgeführt.
Ermittlung bruchmechanischer Kennwerte unter Medieneinfluss zur Bewertung der Spannungsrisskorrosion
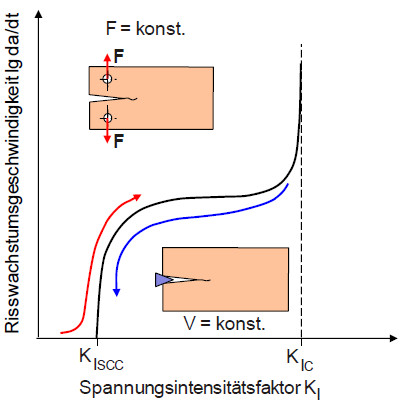
Die prinzipielle Vorgehensweise bei der Versuchsdurchführung ist im Bild 4 dargestellt. Die Beanspruchung des DCB-Prüfkörpers kann hierbei entweder durch eine konstante Belastung (F = konst.) oder über eine konstante Verformung (v = konst.) mittels Keils oder Schrauben aufgebracht werden. Bei F = konst. wird über mehrere unterschiedlich belastete Prüfkörper der KI-Wert bestimmt, der den Beginn der stabilen Rissausbreitung auslöst, wobei die zugehörigen Werte von F und a an die Bestimmungsgleichung für KI einzusetzen sind. Bei v = konst. verringert sich der KI-Wert mit zunehmender Rissverlängerung im korrosiven Medium und bewirkt, dass der Riss zum Stillstand kommt. Zu dieser Risslänge a und der vorliegenden Kerbaufweitung v gehört nach der entsprechenden Bestimmungsgleichung zu berechnende KIscc-Wert. Weitere detaillierte Angaben hinsichtlich Prüfkörperabmessungen sowie zur Versuchsdurchführung können [3] entnommen werden. In Analogie zur Linear-elastischen Bruchmechanik (LEBM) muss auch bei der Bestimmung bruchmechanischer Kennwerte unter Medieneinfluss zur Bewertung der Spannungsrisskorrosion im ebenen Dehnungszustand (EDZ) die Anforderungen an die Geometrie der Prüfkörper kontrolliert werden.
Geometriekriterium für Metalle:
Geometriekriterium für Kunststoffe:
Es gilt: Re = y = Streckspannung (Streckgrenze).
Die Geometriekonstante ist werkstoffabhängig. (siehe auch Geometriekriterium, Bruchzähigkeit)
| Bild 4: | Verlauf der Risswachstumsgeschwindigkeit in Abhängigkeit vom Spannungsintensitätsfaktor und Versuchsdurchführung bei konstanter Belastung bzw. Verformung |
Weitere detaillierte Angaben zu den genannten Prüfmethoden hinsichtlich Prüfkörperabmessungen sowie zur Versuchsdurchführung können [3] und [4] entnommen werden.
Ermittlung von bruchmechanischen Kennwerten an DCB-Prüfkörpern für Faserverbundwerkstoffe
Der DCB-Prüfkörper wurde ursprünglich für bruchmechanische Untersuchungen an Klebverbindungen entwickelt, dann aber auf Unidirektionale (UD)-Laminate übertragen [5].
Prüfnormen:
- ASTM D 5528/D 5528M (2021): Standard Test Method for Mode I Interlaminar Fracture of Unidirectional Fiber-Reinforced Polymer Matrix Composites
- ISO 15024 (2023-02): Fibre-Reinforced Plastic Composites – Determination of Mode I Interlaminar Fracture Toughness, GIc, for Unidirectionally Reinforced Materials
- ISO 25217 (2009-05): Adhesives − Determination of the Mode I Adhesive Fracture Energy of Structural Adhesive Joints using Double Cantilever Beam and Tapered Double Cantilever Beam Specimens
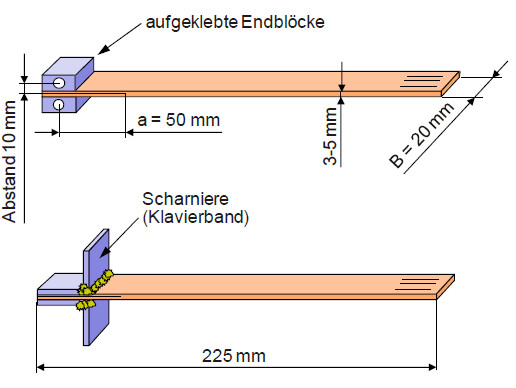
Prüfkörper:
| Bild 5: | DCB-Prüfkörper mit Blöcken (oben) und Scharnieren (unter) zur Krafteinleitung |
L = 225 mm
B = 20 mm
a = 50 mm
Prüfmethode:
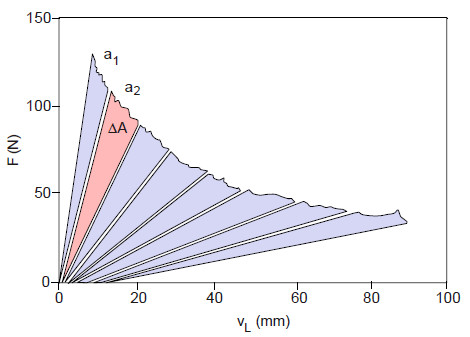
Um einen definierten Anfangriss zu erhalten, wird eine 50 mm lange Folie eingelegt. Charakteristisch für diese Prüfmethode ist eine stabile Rissausbreitung, d. h. der Rissfortschritt kann während des Versuches kontrolliert werden. Es werden entweder Al-Blöcke oder Scharniere zur Krafteinleitung verwendet. Der DCB-Prüfkörper wird in einer Universalprüfmaschine kontinuierlich belastet – in Intervallen von ca. 10 mm wird die Rissöffnung und nach Entlastung die Risslänge registriert. Zur Auswertung existieren mehrere eingeführte Verfahren, von denen hier die Flächenmethode vorgestellt werden soll (siehe Bild 6). Andere Verfahren werden von Hodgkinson in [6] beschrieben. Die kritische Energiefreisetzungsrate GIc wird mit Hilfe der Belastungs-Entlastungs-Kurve gemäß Bild 6 unter Verwendung der nachfolgenden Gleichung ermittelt:
| Bild 6: | Flächenmethode zur Bestimmung von GIc im DCB-Versuch |
Prüfsystem zur Durchführung von DCB-Prüfungen
Für die Durchführung bruchmechanischer Untersuchungen unter Mode I-Beanspruchung an DCB-Prüfkörpern wurde bei der Polymer Service GmbH Merseburg ein in Bild 7 dargestellter Versuchsaufbau realisiert. Das linke Teilbild zeigt den Einbau eines DCB-Prüfkörpers in eine Universalprüfmaschine Z 050 der Fa. ZwickRoell GmbH & Co. KG im unbelasteten Zustand. Im rechten Teilbild wird ein belasteter Zustand mit Rissfortschritt dargestellt.
Ermittlung von bruchmechanischen Kennwerten an DCB-Prüfkörpern für Klebverbindungen
In Arbeiten von M. Schlimmer und Mitarbeitern [7] wird der DCB-Prüfkörper zur bruchmechanischen Bewertung von Klebverbindungen eingesetzt.
Literaturhinweise
| [1] | Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig Stuttgart (1987) 2. Auflage, S. 127–129 und S. 140 (ISBN 3-342-00096-1; siehe AMK-Büchersammlung unter E 29-2) |
| [2] | Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig Stuttgart (1993) 3. Auflage, S. 122–124 (ISBN 3-342-00659-5; siehe AMK-Büchersammlung unter E 29-3) |
| [3] | Heady, R. B.: Evaluation of Sulfide Corrosion Cracking Resistance in Low Alloy Steels. Corrosion 33 (1977) 3, 98–107 |
| [4] | Dietzel, W, Schwalbe, K.-H.: GKSS-Bericht 87/E/46 |
| [5] | Altstädt, V.: Prüfung von Verbundwerkstoffen. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 580/581 (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18) |
| [6] | Hodgkinson, J. M. (Ed.): Mechanical Testing of Advanced Fibre Composites. Woodhead Publishing, Cambridge (2000) |
| [7] | Großkurth, L., Schlimmer, M.: Bruchmechanische Untersuchungen von Dickschichtklebungen. In: Grellmann, W.: Herausforderungen neuer Werkstoffe an die Forschung und Werkstoffprüfung. Deutscher Verband für Materialforschung und -prüfung. Tagungsband 2005, S. 377–382 (ISSN 1861-8154; siehe AMK-Büchersammlung unter A 8) |

![{\displaystyle K_{I}={\frac {E\cdot V\cdot H\left[3H\left(a+0,6H\right)^{2}+H^{3}\right]^{1/2}}{4\left[\left(a+0,6H\right)^{3}+H^{2}a\right]}}}](https://de.wikipedia.org/api/rest_v1/media/math/render/svg/bd4f8344d36331d6adae803f917677767a5c7716)