Dauerschwingversuch
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Dauerschwingversuch
Thermisches Versagen
Die bei einer sinusförmigen Beanspruchung im Dauerschwingversuch je Volumeneinheit aufzubringende Arbeit setzt sich aus zwei Komponenten zusammen, der elastisch gespeicherten Arbeit W', die bei Entlastung als mechanische Arbeit zurückgewonnen wird, und der Verlustarbeit W", die in Wärme umgewandelt wird.
Die Verlustarbeit, bezogen auf 1 Schwingspiel, ergibt sich zu
oder aber je Zeiteinheit zu
Der Verlustwinkel δ ist bei Polymeren im Allgemeinen kleiner als 15°. Deshalb kann sin δ gleich dem Verlustfaktor d = tan δ gesetzt werden, der ebenfalls temperaturabhängig ist. Für den spannungsgeregelten Dauerschwingversuch (σm = const.) folgt dann:
und den dehnungssgeregelten Dauerschwingversuch (εm = const.) ergibt sich:
mit
| E' | Realteil des Elastizitätsmoduls des Dauerschwingversuches |
Der Prüfkörper wird bei schwingender Beanspruchung dann thermisch versagen, wenn die am höchsten beanspruchte Stelle die Erweichungstemperatur erreicht. Dies ist dann der Fall, wenn die durch die innere Dämpfung des Werkstoffs erzeugte Wärme W" größer als die abgeführte Wärmemenge Q ist.
| mit: | α | – | Wärmeübergangszahl |
| f | – | Formfaktor Oberfläche/Querschnitt | |
| ϑ | – | Prüfkörpertemperatur | |
| ϑ1 | – | Umgebungstemperatur | |
| k | – | Korrekturfaktor Innentemperatur |
Damit ergeben sich für das thermische Versagen mit W" > Q für σm = const.
folgende Bedingungen:
und für εm = const.
Der Faktor k berücksichtigt hierin die Temperatur im Prüfkörperquerschnitt.
| k = 1: | Temperatur ist im gesamten Querschnitt gleich |
| k = 0,5: | gute Wärmeleitung |
| k > 1: | Wärmestau |
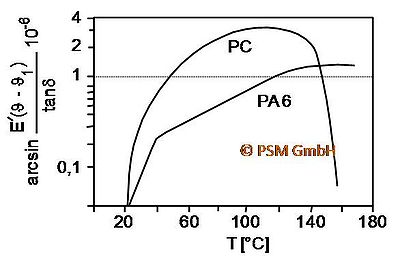
Das Erwärmungsverhalten ist in den einzelnen Kunststoffen sehr unterschiedlich, wie das folgende Bild 1 zeigt.
| Bild 1: | Erwärmung im Dauerschwingversuch an Beispiel von Polycarbonat (Kurzzeichen PC) und Polyamid (Kurzzeichen PA) [1] |
Mit Hilfe der angegebenen Beziehungen kann die Größe der Beanspruchung berechnet werden, bei der keine zusätzliche Erwärmung auftritt bzw. die sich bei gegebener Beanspruchungsgröße einstellende Gleichgewichtstemperatur bestimmt werden.
Können die Wärmeübergangszahl α und der Faktor k nicht aus Erfahrungswerten abgeleitet werden, wird k²/α im Dauerschwingversuch bei konstanter Lastspielzahl N, konstantem Formfaktor f und konstanter Umgebungstemperatur experimentell ermittelt.
Einflüsse
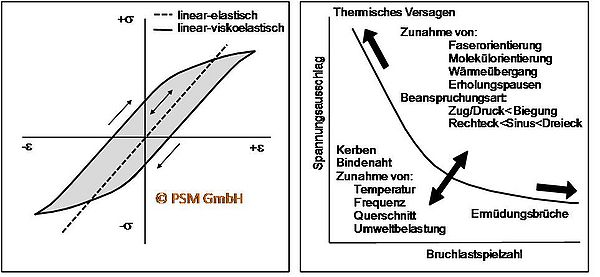
In Kunststoffen verschiebt sich die WÖHLER-Kurve (S-N-Kurve) durch Kerben, Bindenähte, erhöhte Frequenzen, größeren Querschnitt und mediale Beanspruchungen zu niedrigeren Belastungsgrenzen. Eine erhöhte Belastbarkeit ist bei zunehmender Molokülorientierung, in Verbunden bei erhöhter Faserorientierung, bei günstiger Wärmeableitung und bei Belastungspausen zu erwarten (Bild 2).
| Bild 2: | Hysteresis und Einflussfaktoren auf die S-N-Kurve [2] |
Im Allgemeinen wird die Dauerfestigkeit von Kunststoffen nur mit 20 % bis 30 % der Zugfestigkeit angesetzt, für Baustähle liegt dieser Wert dagegen bei 60 % bis 80 %
Bei Anwendung der beschriebenen Versuchsmethode zur Ermittlung der Dauerfestigkeit ist das Deformationsverhalten der zu prüfenden Werkstoffe zu berücksichtigen. Bei Kunststoffen ist das Verformungsverhalten zumindest zeitabhängig, d. h. die wirkende Beanspruchung erzeugt nicht augenblicklich eine entsprechende Deformation, sondern die sich einstellende Deformation läuft zeitlich nach. Bei schwingender Beanspruchung ergibt sich demzufolge im Spannungs-Dehnungs-Diagramm eine Hysterese-Schleife (Hysteresis-Prüfverfahren).
Das bedeutet, dass die durch den Prüfkörper gespeicherte Deformationsarbeit bei der Rückverformung nicht vollständig zurückgewonnen wird, es muss also für die Rückverformung zusätzlich Arbeit aufgebracht werden. Bei jedem Lastspiel wird eine bestimmte Deformationsarbeit aufgenommen. Sie ist proportional der von der Hystereseschleife eingeschlossenen Fläche und wird in Wärme umgesetzt. Dabei spielt die geringe Wärmeleitfähigkeit der Kunststoffe eine wesentliche Rolle. Dauerschwingversuche an Kunststoffen führen also zu einer Erwärmung der Prüfkörper, die einen Abfall des E-Moduls und eine Verstärkung von Kriech- und Relaxationseffekten verursacht.
Um konstante Versuchsbedingungen zu gewährleisten, müssen deshalb die Versuchsparameter überwacht und Abweichungen nachgeregelt werden. Außerdem wird bei Kunststoffen je nach Art, Beanspruchung und Kühlmöglichkeiten die Frequenz auf 500 bis 3000 Lastspiele pro Minute (50 Hz) begrenzt.
Regelung
Die Regelung von Dauerschwingversuchen ist insofern kompliziert, da einerseits die Amplitude (Spannungs- oder Dehnungsausschlag) geregelt werden muss, andererseits bei Kunststoffen infolge der Relaxation oder Retardation die Mittelspannung abnimmt oder die Mitteldehnung zunimmt. Die Regelung der Amplitude entspricht deshalb dem Regelkreis 1 und die des jeweiligen Mittelwertes dem Regelkreis 2. Da aufgrund entstehender Werkstoffschädigungen der E-Modul oder die Compliance nicht konstant bleibt, dieser aber als Grundeinstellparameter dient, kann sich das Regelverhalten ebenfalls verändern. In modernen Prüfanlagen wird deshalb ein 3. Regelkreis implementiert, der zur Überwachung der Steifigkeit des Prüfköpers (siehe: Probennachgiebigkeit) dient und die Regelparameter bei Veränderung kontinuierlich anpasst. Unabhängig von der Darstellung des Signalverhaltens auf dem Monitor des angeschlossenen Computers sollte auf die Überwachung des analogen oder inkrementalen Ausgangssignals mittels eines Oszilloskops nicht verzichtet werden, da die Signalverarbeitung wie Filterung oder Glättung zu einem veränderten Signalverlauf führen kann.
Bei der schwingenden Beanspruchung können folgende Regelgrößen eingestellt werden:
- Proportionale Verstärkung P
- Integrale Verstärkung I
- Derivate Verstärkung D
Insbesondere der P-Anteil besitzt einen großen Einfluss auf die Stabilität der Regelung:
| mit: | A0 | – | Ausgangsamplitude |
| A1 | – | Neuamplitude | |
| Af | – | Regelabweichung der Amplitude | |
| P | – | Proportionalverstärkung |
Die Qualität der Regelung hängt maßgeblich vom Zeitverhalten des Regelkreises ab. Die Differenz aus Soll- und Istsignal (Regelabweichung) wird in Abhängigkeit von der PID-Einstellung verstärkt, integriert und differenziert. Zu hoher P-Anteil führt immer zur Regelkreisinstabilität.
Beispiele
Bei einer Biegebeanspruchung entsteht die Wärme am Ort der größten Spannungen, also der Oberfläche, bei gleichzeitig leichterer Wärmeableitung. Zudem relaxieren die Spannungen dort schneller, so dass insgesamt höherfrequente dynamische Belastungen möglich sind. Werden an der Oberfläche Spannungen abgebaut oder treten sogar Risse auf, wird der Querschnitt und damit das Widerstandsmoment bzw. die Spannungen mit der 2. Potenz abnehmen. Durch die Erniedrigung der Spannung wird der Biegewechselversuch (dehnungsgeregelt) dann auf deutlich niedrigerem Biegespannungsniveau weitergeführt. Biegewechselversuche ergeben daher häufig höhere, fiktive Festigkeiten bei höheren Lastspielzahlen als Zugwechselversuche, da bei spannungsgeregelten Versuchen die Höhe der Belastung konstant bleibt.
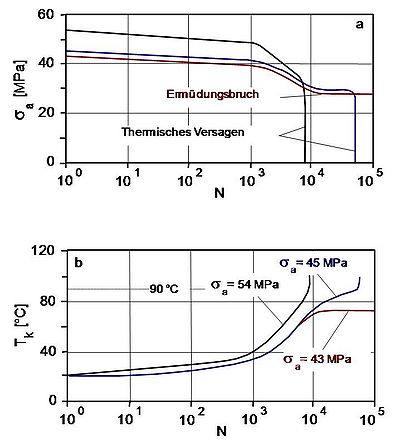
Das nachfolgende Bild 3 zeigt Ergebnisse des Dauerschwingversuchs an Polymethylmethacrylat (Kurzzeichen: PMMA) bei Biegebeanspruchung im Wechselbereich und konstanter Mitteldehnung.
| Bild 3: | Biegeschwingversuch an PMMA; Spannungsamplitude (a), Temperatur an der Prüfkörperoberfläche (b) [3] |
Bei εm und εa = const. fällt die sich zu Beginn des Versuchs einstellende Spannungsamplitude mit zunehmender Lastspielzahl ab. Das gleiche gilt demzufolge für den E-Modul. Gleichzeitig bestimmt die Höhe der sich zu Beginn des Versuchs einstellenden Spannungsamplitude eine Erhöhung der Prüfkörpertemperatur, die zum thermischen Versagen führen kann.
Im gezeigten Beispiel tritt dies bei Spannungsamplituden von 45 MPa und 54 MPa ein, da Prüfkörpertemperaturen von ca. 90 °C entstehen. Bei einer Spannungsamplitude von 43 MPa befinden sich die durch innere Dämpfung entstehende Wärme und die abgeführte Wärme im Gleichgewicht, wodurch sich dann ein Ermüdungsbruch einstellt.
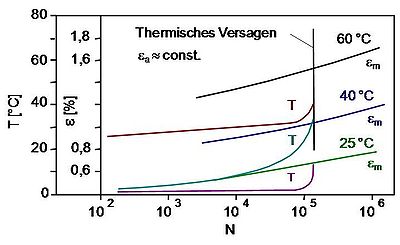
Das nachfolgende Bild 4 zeigt die Ergebnisse von Dauerschwingversuchen im Zugschwellbereich an glasfaserverstärktem Polyamid (Kurzzeichen: PA/GF). Die Lastspielfrequenz betrug 7 Hz, die Spannungsamplitude 36 MPa und die Mittelspannung 38 MPa.
| Bild 4: | Dauerschwingversuch im Zugschwellbereich an PA/GF; Spannungsamplitude (a), Temperatur an der Prüfkörperoberfläche (b) [3] |
Selbst bei dieser niedrigen Frequenz von 7 Hz steigt die Prüfkörpertemperatur oberhalb von 105 Lastwechseln stark an und es kommt zum thermischen Versagen.
Die durch die konstante Mittelspannung bedingte Mitteldehnung nimmt dagegen gleichmäßig zu und die resultierende Dehnungsamplitude bleibt bis zum thermischen Versagen praktisch konstant.
Literaturhinweise
| [1] | Oberbach, K.: Das Verhalten von Kunststoffen bei kurzzeitiger und langzeitiger Beanspruchung, Kennwerte und Kennfunktionen. Materialwissenschaft und Werkstofftechnik 2 (2004) 65, S. 281–291 |
| [2] | Oberbach, K.: Schwingfestigkeit von Thermoplasten – ein Bemessungskennwert ?. Kunststoffe 77 (1987) 4 S. 409–414 |
| [3] | Dallner, C., Ehrenstein, G. W.: Thermische Einsatzgrenzen von Kunststoffen, Teil II: Dynamisch-Mechanische Analyse unter Last. Zeitschrift Kunststofftechnik 2 (2006) 4 S. 1–33 |
Weiterführende Literaturhinweise
- Baur, E., Brinkmann, S., Schmachtenberg, E.: Saechtling Kunststoff-Taschenbuch. Carl Hanser Verlag, München Wien (2008) 30. Auflage (ISBN 978-3-446-40352-9)
- Oberbach, K.: Das Verhalten von Kunststoffen bei kurzzeitiger und langzeitiger Beanspruchung, Kennwerte und Kennfunktionen. Materialwissenschaft und Werkstofftechnik 2 (2004) 65, S. 281–291
- Hellrich, W., Harsch, G., Haenle, S.: Werkstoff-Führer Kunststoffe, Eigenschaften – Prüfungen – Kennwerte. Carl Hanser Verlag, München Wien (2004) 9. Auflage (ISBN 3-446-22559-5)
- Becker, G. W., Braun, D., Carlowitz, B.: Die Kunststoffe. Chemie, Physik, Technologie, Kunststoff-Handbuch Band 1. Carl Hanser Verlag, München, Wien (1990) 1. Auflage (ISBN 978-3-4461-4416-1)
- Ehrenstein, G. W.: Faserverbund-Kunststoffe, Werkstoffe – Verarbeitung – Eigenschaften. Carl Hanser Verlag, München Wien (2006), 2. Auflage (ISBN 978-3-446-22716-3; siehe AMK-Büchersammlung unter G 6-2)
- Bargel, H.-J., Schulze, G.: Werkstoffkunde. Springer Verlag Berlin Heidelberg 11. Auflage (2012) (ISBN 978-3-642-17716-3; siehe AMK-Büchersammlung unter L 43)
- Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 172ff und S. 179ff (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18)
- Erhard, G.: Konstruieren mit Kunststoffen. Carl Hanser Verlag, München (2008) 4. Auflage, (ISBN 978-3-446-41646-8; siehe AMK-Büchersammlung unter G 59)
- Renz, R., Altstädt, V., Ehrenstein, G. W.: Schwingfestigkeitsverhalten von faserverstärkten Kunststoffen (SMC); Faserverbundwerkstoffe. Band III, Springer Verlag, Berlin (1986), S. 441–518 (ISBN 978-3-642-82624-5)
- Oberbach, K.: In Henkhaus, R.: Schwingfestigkeit von Kunststoffen. DVM, 1. Sitzung des AK „Polymerwerkstoffe“ Frankfurt/M., 21. Und 22. Oktober 1986, Tagungsband S. 25–40 (siehe AMK-Büchersammlung unter C 15)









![{\displaystyle A_{1}-A_{0}\,=\,\left[1-{\frac {A_{f}}{100}}\right]P}](https://de.wikipedia.org/api/rest_v1/media/math/render/svg/60d70f66b365133b2a067f2a94ba5aeb8065f455)