Ermüdung

Ein Service der
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung
PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Ermüdung

Grundlagen

Im praktischen Einsatz sind Bauteile neben statischen Beanspruchungen häufig auch schwingenden Belastungen ausgesetzt. Diese werden oftmals auch als dynamische Beanspruchung bezeichnet, die aber von stoßartigen Belastungen (siehe: Schlagbeanspruchung Kunststoffe) prinzipiell abgegrenzt werden müssen. Selbst wenn diese schwingenden Beanspruchungen im linear-elastischen bzw. linear-viskoelastischen Bereich liegen, können diese bei wesentlich niedrigeren Spannungen und Dehnungen als beim statischen Lastfall zum Versagen des Bauteils führen.

Überschreitet die Dehnungsamplitude die Grenze der linearen Viskoelastizität, treten Schädigungen z. B. als Mikrorisse auf. Statische Festigkeits- und Deformation­skennwerte dürfen deshalb nicht zur Dimensionierung (siehe: Kunststoffbauteil, Dimensionierung) schwingend beanspruchter Konstruktionsteile verwendet werden.

Spannungs- und Dehnungsgeregelter Dauerschwingversuch

Schwingende Beanspruchung heißt periodisch wechselnde Beanspruchung und das Prüfverfahren zur Ermittlung von Kennwerten unter dieser Beanspruchungsart wird als Dauerschwingversuch bezeichnet. Dabei werden zwei unterschiedliche Varianten unterschieden:

• Spannungsgeregelter Dauerschwingversuch bei dem einer konstanten Spannung eine konstante Spannungsamplitude überlagert wird (Eliminierung der Spannungsrelaxation erforderlich)
• dehnungsgeregelter Dauerschwingversuch bei dem einer konstanten Dehnung eine konstante Dehnungsamplitude überlagert wird (Eliminierung des Kriechens unter Last erforderlich)

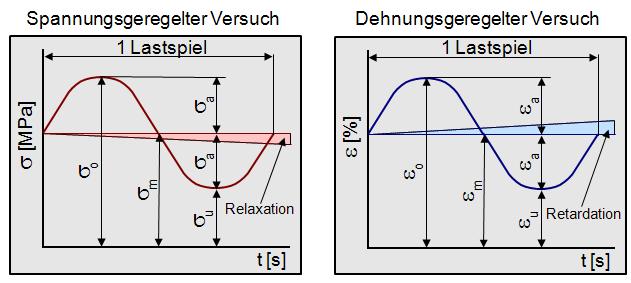
Diese Überlagerung der zu Beginn des Versuches erzeugten Spannung bzw. Dehnung mit einer periodischen Spannungs- oder Dehnungsamplitude wird im nachfolgenden Bild 1 grafisch dargestellt.

Bild 1:

Spannungs-Zeit- und Dehnungs-Zeit-Schaubild bei schwingender Beanspruchung $\sigma$o Oberspannung $\epsilon$o Oberdehnung $\sigma$u Unterspannung $\epsilon$u Unterdehnung $\sigma$m Mittelspannung $\epsilon$m Mitteldehnung $\sigma$m Spannungsausschlag $\epsilon$m Dehnungsausschlag

Ein vollständiger Beanspruchungszyklus wird als Lastspiel oder Schwingspiel bezeichnet. Die Mittelspannung (Mitteldehnung) $\sigma$_m ($\epsilon$_m) ist die bereits erwähnte Vorspannung (Vordehnung), $\sigma$_a ($\epsilon$_a) charakterisieren die Amplitude der überlagerten Spannung (Dehnung), $\sigma$_o ($\epsilon$_o) und $\sigma$_u ($\epsilon$_u) den größten bzw. kleinsten in einem Schwingspiel auftretenden Spannungs- (Dehnungs-) Wert.

Arten von Schwingungen

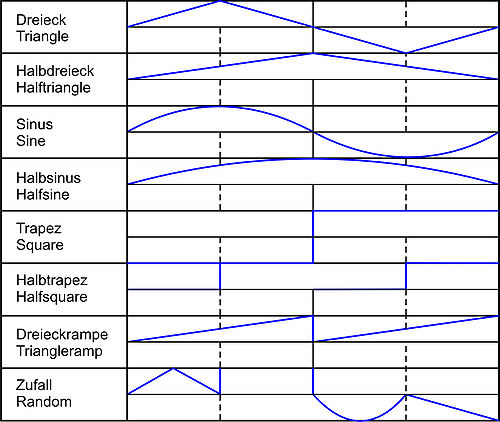
In der prüftechnischen Praxis können folgende Arten von Schwingungen realisiert werden (siehe auch Bild 2):

• Dreieckschwingung (Triangle)
• Halbdreieckschwingung (Halftriangle)
• Sinusschwingung (Sine)
• Halbsinusschwingung (Halfsine)
• Rechteck- oder Trapezschwingung (Square)
• Halbtrapezschwingung (Halfsquare)
• Dreieckrampe (Triangleramp)
• Zufallsschwingung (Random)

Bild 2:

Arten von Schwingungen beim Dauerschwingversuch

Beanspruchungsfälle bei einer Sinusschwingung

In der Prüfpraxis wird zumeist die Sinusschwingung bevorzugt, da sie die höchste Regelkreisstabilität besitzt.

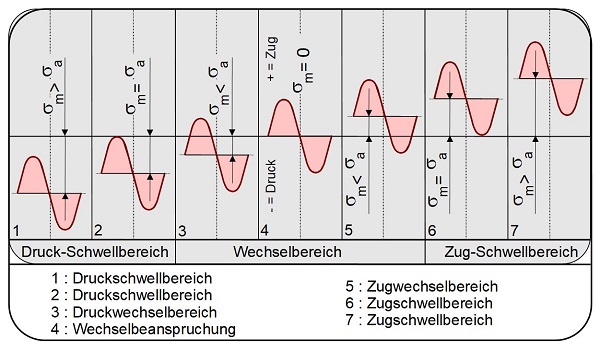
In Abhängigkeit von den Beanspruchungswerten kann dieser sogenannte Einstufen-Dauerschwingversuch in drei Beanspruchungsbereichen mit insgesamt sieben Beanspruchungsfällen durchgeführt werden (Bild 3).

Bild 3:

Beanspruchungsfälle und -bereiche beim Dauerschwingversuch

Je nach Versuchsdurchführung werden entweder die Mittelspannung und die Spannungsamplitude oder die Ober- und Unterspannung als Beanspruchungswerte vorgegeben. Im spannungsgeregelten Dauerschwingversuch wird das Spannungsverhältnis R = $\sigma$_u / $\sigma$_o als Kenngröße angegeben. Dabei ist zu unterscheiden zwischen:

• Zugschwellbereich $\sigma$_o und $\sigma$_u sind positiv; $\sigma$_m ≥ $\sigma$_a; 0 ≤ R < +1,
• Wechselbereich $\sigma$_o und $\sigma$_u haben entgegengesetzte Vorzeichen; $\sigma$_m < $\sigma$_a; 0 ≤ R < -1 und
• Druckschwellbereich $\sigma$_o und $\sigma$_u sind negativ; $\sigma$_m ≥ $\sigma$_a; 0 ≤ R < +1.

Bestimmung der Dauerfestigkeit

Wird von einer konstanten Mittelspannung ausgegangen besteht das Ziel des Versuchs darin, die Dauerschwingfestigkeit oder Dauerfestigkeit $\sigma$_D zu ermitteln. Die Dauerfestigkeit $\sigma$_D charakterisiert die größte Spannungsamplitude $\sigma$_a, die ein Prüfkörper unendlich oft und ohne unzulässige Verformungen aushält. Bei allen Spannungsamplituden oberhalb $\sigma$_D erfolgt der Bruch des Prüfkörpers. Zur praktischen Bestimmung von $\sigma$_D kann der WÖHLER-Versuch zur Ermittlung von S-N-Kurven durchgeführt werden, der die Abhängigkeit zwischen Beanspruchungshöhe und ermittelter Bruchschwingspielzahl wiedergibt. Der WÖHLER-Versuch wird bei Kunststoffen bis zu Schwingspielzahlen von N ≥ 10⁷ durchgeführt.

Hinweise über die zur experimentellen Ermittlung des Ermüdungsverhaltens verwendeten Prüfkörperformen sind unter Prüfkörper für Ermüdungsversuche zu finden.

Siehe auch

• Dauerschwingversuch
• Prüfkörper für Ermüdungsversuche
• Dauerfestigkeit
• Schwingungsinduzierter Kriechbruch
• Schwingungsbruch

Literaturhinweise

• DIN 50100 (2022-12): Schwingfestigkeitsversuch – Durchführung und Auswertung von zyklischen Versuchen mit konstanter Lastamplitude für metallische Werkstoffproben und Bauteile
• DIN 53442 (1990-09): Prüfung von Kunststoffen – Dauerschwingversuch im Biegebereich an flachen Prüfkörpern
• DIN EN ISO 3385 (2014-10): Weich-elastische polymere Schaumstoffe – Bestimmung der Ermüdung im Dauerschwingversuch mit Stoßbelastung unter konstanter Kraft
• Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024) 4. Auflage, S. 164–174 (ISBN 978-3-446-44718-9; E-Book: ISBN 978-3-446-48105-3; siehe AMK-Büchersammlung unter A 23)
• Bierögel, C., Grellmann, W.: Fatigue Loading. In: Grellmann, W., Seidler, S.: Mechanical and Thermomechanical Properties of Polymers. Landolt-Börnstein. Volume VIII/6A3, Springer Verlag, Berlin (2014) 241–285 (ISBN 978-3-642-55165-9; siehe AMK-Büchersammlung unter A 16)