Frequenzanalyse

Ein Service der
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung
PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Frequenzanalyse

Fourierreihe und Fouriertransformation

Die Interpretation eines Zeitsignals kann mit Hilfe von Transformation durchgeführt werden. Jede periodische Funktion lässt sich als eine Summe aus Sinus- und Kosinustermen in Form einer Fourierreihe schreiben. Dabei drücken die Fourier-Koeffizienten A_k und B_k aus, in welcher Weise die Amplituden der einzelnen Terme gewichtet und die Phase verschoben werden müssen, um die Ausgangsfunktion zu beschreiben.

$U\left(t\right)\,=\,\sum _{k=0}^{\infty }\left(A_{k}\cdot \cos \omega _{k}t\,+\,B_{k}\cdot \sin \omega _{k}t\right),B_{0}\,=\,0$,

$\omega _{k}\,=\,{\frac {2\pi \cdot k}{T}}$, mit dem auftretenden Frequenzschema $\omega \,=\,0,\,{\frac {2\pi }{T}},\,{\frac {4\pi }{T}},\,{\frac {6\pi }{T}},\,...$

Die Kreisfrequenz $\omega$_k wird dabei nach der unteren Gleichung berechnet, mit T als Periode der Funktion U(t). Bei der Superposition von Sinus- und Kosiniusfunktionen kommen nur ganzzahlige Vielfache der Grundfrequenz, gemäß dem dargestellten Schema, vor (2$\pi$-periodische Funktionen) [1].

Nichtperiodische transiente Signale, deren Signalamplitude infolge der Dämpfung in endlicher Zeit gegen Null geht, können mit Hilfe der Fouriertransformation analysiert werden. Diffenziert wird dabei zwischen der kontinuierlichen und diskreten Fouriertransformation (DFT). Der Unterschied liegt im zeitlichen Signalverlauf, der im Falle einer diskretisierten Funktion, im Gegensatz zur kontinuierlichen Funktion, nur zu N diskreten Zeiten bekannt ist.

$t_{k}\,=\,k\cdot \Delta t,\,k\,=\,0\,...\,N-1\,mit\,N\,eine\,Potenz\,von\,2\,$

Außerhalb des gesampelten Intervalls T = N $\Delta$t ist die Funktion und deren Verlauf unbekannt. Dies trifft für jede digitale Datenaufnahme zu. Aus diesem Grund wird die Annahme gemacht, dass außerhalb des betrachteten Intervalls die Funktion periodisch fortgesetzt wird [1, 2]. Die Fouriertransformation stellt ein Signal spektral, d. h. in seinem Frequenzinhalt dar, dabei gilt die Fouriertransformierte U'(f) an, mit welcher Amplitude die jeweilige Frequenz im Signal enthalten ist:

$U'\left(f\right)\,=\,\int _{-\infty }^{\infty }U\left(t\right)\cdot e^{2\pi \cdot i\cdot f\cdot t}dt$

Es wird vorausgesetzt, dass es sich um ein stationäres, d. h. nicht kurzfristig änderndes Signal handelt. Als Ergenbis der Transformation steht die globale Frequenzinformation ohne zeitliche Zuordenbarkeit zur Verfügung. Die schnelle Fouriertransformation (FFT) ist ein optimierter Algorithmus für die DFT.

Kurzzeit-Fouriertransformation

Der Nachteil des Verlustes der zeitlichen Information eines Signals ist durchaus von größerer technischer Bedeutung, da für die betrachteten Signale die zugrunde liegenden Ursachen und Zuordnung zum Ursprungssignal von Interesse sind. Eine Verbesserung im Hinblick auf die Zeitauflösung bietet die Kurzzeit-Fouriertransformation (Short Time Fourier Transform – STFT), auch gefensterte Fouriertransformation (Windowed Fourier Transform – WFT) genannt. Das Siganl wird in kleine Zeitbereiche aufgeteilt, die dann einzeln transformiert werden. Dazu wird das Signal mit einer Fensterfunktion w multipliziert und es werden für das betrachtete Signal die Fourier-Koeffizienten berechnet. Durch diese Fensterung ist eine zeitliche Einteilung der Spektren möglich. Probleme ergeben sich in zweierlei Hinsicht. An den Fensterkanten liegt durch die abrupte Änderung der Amplituden im Zeitbereich eine Unstetigkeit vor, was eine Überlappung der Fenster bedingt. Ein weiterer Nachteil der gefensterten Fouriertransformation liegt in der willkürlich zu wählenden Fensterbreite. Ein enges Fenster ermöglicht eine gute zeitliche Auflösung, bedingt aber maximal detektierbare Frequenzen, welche mit einer vollen Periode in das Zeitfenster passen müssen. Umgekehrt wird bei einem breiten Fenster die Frequenzauflösung verbessert, aber gleichzeitig die zeitliche Auflösung herabgesetzt.

Wavelet-Transformation

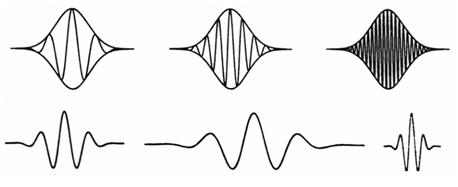
Der Nachteil der gegenläufigen Zeit- und Frequenzauflösung bei der gefensterten Fouriertransformation wird bei der Wavelet-Transformation dadurch vermieden, dass die Fensterbreite variabel ist und die Anzahl der Oszillationen im Fenster konstant ist (siehe Bild).

Bild:

Frequenzanalyse im Fourier-Raum (oben) bei der Verwendung einer gefensterten Fouriertransformation und im Wavelet-Raum (unten) durch Dehnen und Stauchen eines Mother-Wavelets (links unten) [3]

Damit wird einerseits eine Änderung der Fensterbreite, d. h. der zeitbasis, und andererseits die notwendige Frequenzvariation erreicht. das Dehnen und Stauchen des Wellenzuges wurde von Morlet [3, 4] Wavelet genannt, wobei die Form der verwendeten Ausgangsfunktion (Mother-Wavelet) erhalten bleibt. das Wort Wavelet ist eine Neuschöpfung aus dem franz. Wort "ondelette", was kleine Welle bedeutet, welches teils wörtlich ("onde" $\rightarrow$ "wave"), teils phonetisch ("-lette" $\rightarrow$ "-let") ins Englische übertragen wurde und so auch im Deutschen verwendet wird. Für die Wavelet-Transformierte W eines Zeitsignals f und für das Gabor-Wavelet sowie für die Fouriertransformierte gelten die nachfolgend aufgeführten Gleichungen [5]. Analog zu der Fouriertransformation geben die Koeffizienten a und b an, wie die zur Analyse verwendete Wavelet-Funktion $\Psi$ verändert werden muss, damit das Signal mit der Wavelet-Funktion $\Psi$ berechnet werden kann. Die Parameter a und b beschreiben dabei die Dehnung bzw. Stauchung sowie die Verschiebung der Mother-Wavelets. Das Integral über ein Wavelet ist vereinbarungsgemäß stets null, so dass man als Produkt eines Wavelets mit einer Konstanten ebenfalls null erhält [5, 6]. $\omega$_p ist die Mittelfrequenz und $\gamma$ eine Konstante, welche eingeführt wird, damit die Zuverlässigkeitsbedingung erfüllt ist, d. h. mit der Konstante $\gamma$ wird sichergestellt, dass es sich um ein Orthonormalsystem handelt. Aus der Fouriertransformation wird die halbwertszeit 2 $\gamma$ / $\omega$_p für das Gabor-Wavelet sowie die Halbwertsfrequenz 1/2 $\omega$_p / $\gamma$ ermittelt. Im Ergebnis steht eine Ansammlung von Waveletkoeffizienten (WT-Koeffizienten), wobei jeder Koeffizient durch die Parameter a und b definiert und somit der Frequenz und Zeit zuordenbar ist.

$W\,f\left(a{,}b\right):=\left\langle f{,}\Psi _{a{,}b}\right\rangle \,=\,{\frac {1}{\sqrt {\left|a\right|}}}\cdot \int _{-\infty }^{\infty }\,f\left(t\right)\Psi \left({\frac {t-b}{a}}\right)dt$

$\Psi \left(t\right)\,=\,\pi ^{-{\frac {1}{4}}}\cdot \left({\frac {\omega _{p}}{\gamma }}\right)^{\frac {1}{2}}\cdot \exp \left[-{\frac {t^{2}}{2}}\cdot \left({\frac {\omega _{p}}{\gamma }}\right)^{2}+i\omega _{p}\cdot t\right]$

${\hat {\Psi }}\left(\omega \right)\,=\,\left(2\cdot \pi \right)^{\frac {1}{2}}\cdot \pi ^{-{\frac {1}{4}}}\cdot \left({\frac {\omega _{p}}{\gamma }}\right)^{\frac {1}{2}}\cdot \exp \left[-{\frac {t^{2}}{2}}\cdot \left({\frac {\omega _{p}}{\gamma }}\right)^{2}\cdot \left(\omega -\omega _{p}\right)^{2}\right]$

$\gamma \,=\,\pi \cdot \left({\frac {2}{\ln 2}}\right)^{\frac {1}{2}}\,=\,5{,}336$

Die Darstellung als Kontourkarte (Spektrogramm oder Voiceprint) zeigt, wie die Signalintensität der einzelnen Frequenzen sich mit der Zeit ändert damit im hier betrachteten Fall die charakteristischen Eigenschaften des akustischen Signals auf einen Blick [7].

Siehe auch

• IKBV mit SEA
• Schallemissionsanalyse
• Elastizitätsmodul
• Schubmodul

Literaturhinweise

[1]	Butz, T.: Fourietransformation für Fußgänger. B. G. Teubner, Stuttgart Leipzig Wiesbaden (2003) 3. Auflage, (ISBN 3-519-20202-6)
[2]	Blatter, C.: Wavelets: Neuartige Bausteine der konstruktiven Analysis. 22. Eichstätter Kolloquium zur Didaktik der Mathematik, Katholische Universität Eichstätt-Ingolstadt, 23. Februar 2006
[3]	Hubbard, B. B.: Wavelets – Die Mathematik der kleinen Wellen. Birkhäuser Verlag, Basel Boston Berlin (1997) (ISBN 978-3764356880)
[4]	Goupillaud, P., Grossmann, A., Morlet, J.: Cycle-octave and Related Transforms in Seismic Analysis. Geoexploration, 23 (1984) 85–102
[5]	Blatter, C.: Wavelets – Eine Einführung. Friedr. Vieweg & Sohn Verlagsgesellschaft mbH, Braunschweig/Wiesbaden (2003) (ISBN 978-3-528-16947-3; e-Book: ISBN 978-3-663-11817-6)
[6]	Grosse, C. U., Ruck, H.-J., Bahr, G.: Analyse von Schallemissionssignalen unter Verwendung der Wavelet-Transformation. 13. Kolloquium Schallemission, Jena, 27. – 28.09.2001
[7]	Suzuki, H., Kinjo, T., Hayashi, Y., Takemoto, M., Ono, K.: Wavelet Transform of Acoustic Emission Signals. Journal of Acoustic Emission 14 (1996) 69–84