Kunststoffbauteil
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Kunststoffbauteil, Dimensionierung
Allgemeines
Für den Konstrukteur von Erzeugnissen aus Kunststoffen besteht in zunehmenden Maße die Aufgabe darin, die Werkstoffauswahl, die Dimensionierung und Konstruktion sowie die Gestaltung von Bauteilen mit wissenschaftlich begründeten, kunststoffspezifischen Arbeitsmethoden durchzuführen.
Festigkeits- und Verformungsnachweis
Die gegenwärtige Vorgehensweise bei der Dimensionierung von Bauteilen aus Kunststoffen ist dadurch gekennzeichnet, dass bei der Festlegung der beanspruchten Querschnitte und ihrer Geometrie zulässige Spannungen σzul oder zulässige Verformungen εzul als Entscheidungskriterien dienen. Dabei wird der in der Regel mehrachsige Spannungszustand der Konstruktion mit Hilfe einer Vergleichsspannungshypothese mit einer zulässigen werkstoffabhängigen Spannung verglichen [1–3]. Diese zulässige Spannung ergibt sich z. B. bei der Dimensionierung gegenüber der Streckspannung σy zu
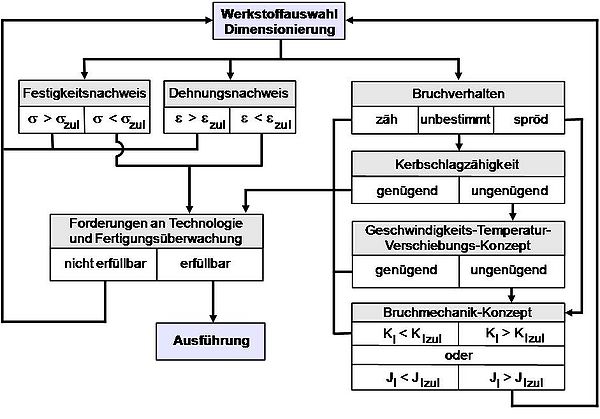
worin p einen Sicherheitsbeiwert darstellt, der Unsicherheiten in den Werkstoffeigenschaften, z. B. Chargeneinflüsse sowie Unzulänglichkeiten in den Berechnungsverfahren (Lastannahmen u. ä., Gefährdung von Menschen und Eigentum), enthält. Bei der Dimensionierung gegenüber der Dehnung ist eine analoge Vorgehensweise möglich. Unter Berücksichtigung der bei der Konstruktion vorausgesetzten Anforderungen an die technologische Realisierung und ihre Kontrolle bei der Fertigungsüberwachung wird dann die Ausführung der Konstruktion möglich, wobei Aspekte der Zähigkeit hier nicht berücksichtigt werden. Diese Vorgehensweise wird im linken Teil des Bildes schematisch dargestellt.
| Bild: | Schema zur Bewertung der Zähigkeitseigenschaften von Erzeugnissen aus Kunststoffen |
Zähigkeitsnachweis
Die ersten Ansätze zur Berücksichtigung von Gesichtspunkten des Werkstoffversagens durch Sprödbruch (siehe Brucharten) bei der Dimensionierung existieren für die Zähigkeitsbewertung von Rohren [4–8]. Dabei liefert die Verwendung der Kerbschlagzähigkeit acN zur Ermittlung der Bruchenergie keinen wesentlichen Fortschritt in der Aussagekraft [5, 6]. Der wichtigste Nachteil der Kerbschlagzähigkeit ist, dass es sich um eine integrale Kenngröße handelt und keine Spannungs- und Dehnungswerte angegeben werden können, d. h. Kerbschlagzähigkeitswerte gestatten nur eine qualitative Bewertung der Werkstoffe, denn die Übertragung der am Prüfkörper gewonnenen Ergebnisse auf Konstruktionen ist nicht möglich. Ein zusätzliches Problem ist mit den bei gefüllten und verstärkten Kunststoffen in Schlagkraft-Durchbiegungs-Diagrammen auftretenden Rissverzögerungsenergien (siehe: Instrumentierter Kerbschlagbiegeversuch und IKBV Typen von Schlagkraft-Durchbiegungs-Diagrammen) verbunden [5].
Da die Sprödbruchempfindlichkeit neben dem Spannungszustand auch durch die Temperatur und die Beanspruchungsgeschwindigkeit beeinflusst wird und der Sprödbruch (siehe: Brucharten) im elastischen und viskoelastischen Bereich erfolgt, sind Vorstellungen entwickelt worden, um die Eigenschaftsänderungen abzuschätzen, die bei den infolge von Schlag oder Stoß auftretenden hohen Dehngeschwindigkeiten (siehe Dehnrate Grundlagen) in den elastischen Kenngrößen E und G zu erwarten sind. Dies wird mit Hilfe des Zeit-Temperatur-Verschiebungsgesetzes [9] realisiert. Dieses Gesetz beinhaltet eine Korrelation zwischen der Beanspruchungszeit und -temperatur und gestattet es, die bei definierten Temperaturen oder Beanspruchungszeiten gewonnenen Messwerte auf andere Zeiten und Temperaturen zu übertragen.
Diese Arbeitsweise ermöglicht dann z. B. aus der Dehnungsgeschwindigkeit dε/dt (siehe Dehnrate Applikationen) unter Berücksichtigung der durch die Geschwindigkeit bedingten Verschiebung der Elastizitätsmodul-Temperatur-Kurve, die Belastungsgeschwindigkeit dσ/dt zu ermitteln und mit Belastungsgeschwindigkeiten zu vergleichen, wie sie z. B. im Fallversuch auftreten. Auf diese Weise ist es möglich, die für die Beurteilung der Sprödbruchanfälligkeit (siehe Sprödbruchfördernde Faktoren) zur Verfügung stehenden Informationen besser auszuschöpfen.
Sprödbruchsicherheitsnachweis mit bruchmechanischen Kenngrößen
Ein in Analogie zum Festigkeits- oder Verformungsnachweis durchführbarer Sprödbruchsicherheitsnachweis ist mit Hilfe der Konzepte der Bruchmechanik möglich. Für die funktions- oder fertigungsbedingten Kerben (Nuten, Querschnittsänderungen usw.) im Formteil (siehe: Formmasse) ist aus der zu erwartenden Belastung mit Hilfe der FEM [10] ein Spannungsintensitätsfaktor [11] bzw. bei größeren plastischen Verformungen, wie sie i. Allg. bei Kunststoffen auftreten, ein J-Wert durch numerische Integration zu berechnen. Dieser Spannungsintensitätsfaktor bzw. J-Wert muss kleiner sein als der zulässige Spannungsintensitätsfaktor KIzul bzw. der zulässige Wert JIzul. Die zulässigen Kennwerte für die Zähigkeit berechnen sich aus den ermittelten geometrieunabhängigen Werkstoffkennwerten KId und JId (siehe Geometriekriterium) nach den Gleichungen
worin q1 und q2 Sicherheitsbeiwerte darstellen, welche die Unsicherheiten in der Modellbildung und in den Werkstoffeigenschaften berücksichtigen [4].
Zur Gewährleistung einer hohen technischen Sicherheit und Zuverlässigkeit werden bei der Werkstoffauswahl und Dimensionierung auf Grund des elastisch-plastischen Bruchverhaltens in verstärktem Maße Auswertemethoden der Fließbruchmechanik (FBM) Anwendung finden.
Übertragbarkeit Prüfkörper – Bauteil
Trotz des allgemein anerkannten Wissenstandes zur Übertragbarkeit der an kleinen Prüfkörpern (Standardprüfkörpern) ermittelten geometrieunabhängigen bruchmechanischen Kennwerte [5, 6, 12] sind weiterführende Untersuchungen zur Bewertung des Bruchverhaltens (siehe Geometriekriterium) von Halbzeugen und Fertigteilen erforderlich, um die Aussagefähigkeit der Versagenskonzepte der Fließbruchmechanik zu bestätigen (siehe auch: Erkenntnisniveauebenen der Bruchmechanik)
Literaturhinweise
| [1] | Erhard, G.: Konstruieren mit Kunststoffen, Carl Hanser Verlag, München Wien (1993) 1. Ausgabe, S. 99–108 (ISBN 3-446-17397-8; siehe AMK-Büchersammlung unter G 33) |
| [2] | Ehrenstein, G. W.: Mit Kunststoffen konstruieren – Eine Einführung. Carl Hanser Verlag, München Wien (2007) (ISBN 978-3-446-41322-1; siehe AMK-Büchersammlung unter G 42) |
| [3] | Michaeli, W., Brinkmann, T., Lessenich-Henkys, V.: Kunststoff-Bauteile werkstoffgerecht konstruieren. Carl Hanser Verlag, München Wien (1995) |
| [4] | May, M., Hoffmann, H., Grellmann, W.: Anwendungen der dynamischen Bruchzähigkeit zur Beurteilung der Zähigkeitseigenschaften. Plaste und Kautschuk 31 (1984) 1, S. 26–30 Download als pdf |
| [5] | Grellmann, W.: Bewertung der Zähigkeitseigenschaften durch bruchmechanische Kennwerte. In: Schmiedel, H. (Hrsg.): Handbuch der Kunststoffprüfung. Carl Hanser Verlag, München Wien (1992) 139–183, (ISBN 978-3446163362; siehe AMK-Büchersammlung unter A 3) |
| [6] | Grellmann, W., Seidler, S. (Eds.): Deformation and Fracture Behaviour of Polymers. Springer Verlag, Berlin Heidelberg (2001) (ISBN 978-3540412472; siehe AMK-Büchersammlung unter A 7) |
| [7] | Jungbluth, M.: Untersuchungen zum Verformungs- und Bruchverhalten von PVCC-Werkstoffen. Dissertation, TH Leuna-Merseburg (1987) (siehe AMK-Büchersammlung unter B 1-1) (Kurzzusammenfassung/Inhaltsverzeichnis) |
| [8] | Brown, N., Lu, X.: The Dependence of Rapid Crack Propagation in Polyethylene Pipes on the Plane Stress Fracture Energy of the Resin. Polymer Engng. and Science 41 (2001) 1140–1145 |
| [9] | Menges, G., Schlüter, H., Jonas, R.: Ermittlung von Werkstoff- sowie Festigkeitskennzahlen für die Konstruktion und Dimensionierung von spritzgegossenen Kunststofferzeugnissen. Forschungsbericht des Landes Nordrhein-Westfalen Nr. 2892 Köln/Opladen, Westdeutscher Verlag, 1979 |
| [10] | Rossmanith, H.-P. (Hrsg.): Finite Elemente in der Bruchmechanik. Springer Verlag, Berlin Heidelberg (1982) (ISBN 978-3-7091-2297-6) |
| [11] | Tada, H., Paris, P. C., Irwin, G. R.: The Stress Analysis of Cracks Handbook. 3th Ed., ASME Press, New York (2000) |
| [12] | Grellmann, W., Seidler, S., Lach, R.: Geometrieunabhängige bruchmechanische Werkstoffkenngrößen – Voraussetzung für die Zähigkeitscharakterisierung von Kunststoffen. Materialwissenschaften und Werkstofftechnik 32 (2001) S. 552–561 |