Mehrachsiger Spannungszustand

Ein Service der
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung
PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Mehrachsiger Spannungszustand

Beschreibung des Spannungs- und Dehnungszustandes

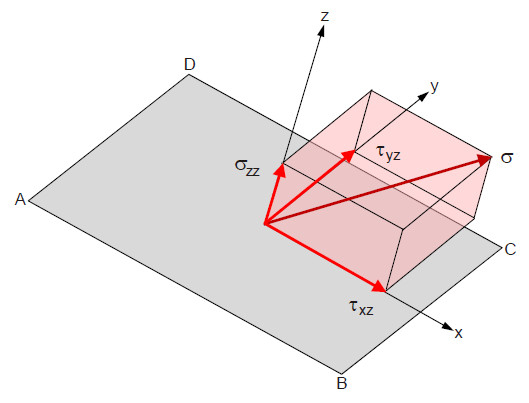
Im allgemeinen Belastungsfall, wenn der Spannungsvektor (Kraftvektor je Einheitsfläche) und die Bezugsebenennormale weder parallel noch senkrecht zueinander orientiert sind, ist mit Hilfe der Regeln der Vektorrechnung eine Zerlegung der Spannung in eine Normalspannungskomponente σ_zz und zwei senkrecht zueinander stehende Scherspannungskomponenten τ_xz und τ_yz möglich (Bild 1).

Bild 1:

Zerlegung der an der Bezugsebene ABCD angreifenden Spannung σ in Normalspannungskomponente σzz und Scherspannungskomponenten τxz und τyz

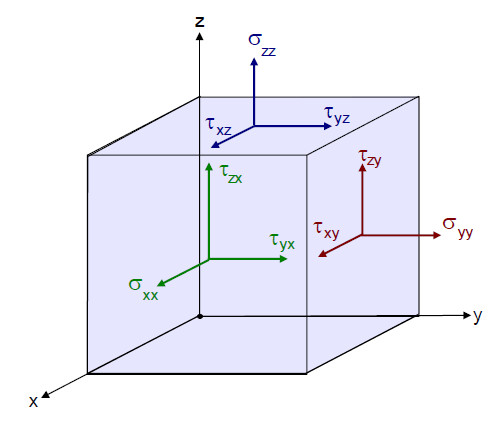
Bei komplexeren Beanspruchungsfällen ist es allerdings notwendig, den räumlichen Spannungs- und Dehnungszustand unabhängig von einer konkreten Bezugsebene zu beschreiben. Hierzu sind neun Spannungskomponenten erforderlich, die an den Schnittflächen eines infinitesimal kleinen würfelförmigen Volumenelementes entsprechend dem Bild 2 angreifen. Entsprechend der Schnittreaktionen des Kräftegleichgewichts wirken an den gegenüberliegenden Flächen des Volumenelementes Spannungen gleicher Größe, jedoch mit entgegengesetztem Richtungssinn.

Die entstehenden Spannungskomponenten können in Form einer Matrix als Elemente eines symmetrischen Tensors zweiter Stufe dargestellt werden (Bild 2):

$\sigma _{ij}={\begin{bmatrix}\sigma _{xx}&\tau _{xy}&\tau _{xz}\\\tau _{yx}&\sigma _{yy}&\tau _{yz}\\\tau _{zx}&\tau _{zy}&\sigma _{zz}\end{bmatrix}}$

(1)

Bild 2:

Räumlicher Spannungszustand des Volumenelements

Die Symmetrie des Spannungstensors

Infolge der Symmetrieeigenschaften des Tensors (σ_ij = σ_ji) reduziert sich die Zahl der voneinander unabhängigen Spannungskomponenten auf sechs.
Durch eine Koordinatentransformation ist es möglich, die Größe der Spannungskomponenten in Bezug auf unterschiedlich orientierte Koordinatensysteme x, y, z zu berechnen. Besondere Bedeutung kommt dabei dem Koordinatensystem zu, bezüglich dessen alle Scherspannungskomponenten des Spannungstensors verschwinden (τ_ij = 0 für alle i ≠ j). Die Achsen dieses Koordinatensystems werden als Hauptachsen 1, 2, 3 und die verbleibenden Normalspannungen (σ_ij mit i = j) als Hauptspannungen σ₁, σ₂, σ₃ bezeichnet. Eine von der Wahl des Koordinatensystems unabhängige Beschreibung des Spannungszustandes ist anhand der Invarianten I₁, I₂ und I₃ des Spannungstensors möglich:

$I_{1}=\sigma _{xx}+\sigma _{yy}+\sigma _{zz}\!$ $I_{2}=\sigma _{xx}\sigma _{yy}+\sigma _{yy}\sigma _{zz}+\sigma _{zz}\sigma _{xx}-\tau _{xy}^{2}-\tau _{yz}^{2}-\tau _{zx}^{2}$ $I_{3}=\sigma _{xx}\sigma _{yy}\sigma _{zz}+2\tau _{xy}\tau _{yz}\tau _{zx}-\sigma _{xx}\tau _{yz}^{2}-\sigma _{yy}\tau _{zx}^{2}-\sigma _{zz}\tau _{xy}^{2}$

(2)

Hinsichtlich der Wirkung der Spannungen kann zwischen Volumen- und Gestaltänderungen unterschieden werden. Dementsprechend kann der Spannungstensor in eine hydrostatische Komponente (Dilatationsanteil) p (Gl. 3):

$p={\frac {1}{3}}(\sigma _{xx}+\sigma _{yy}+\sigma _{zz})={\frac {I_{1}}{3}}$

(3)

und eine deviatorische Komponente (Gestaltänderungsanteil) σ_ij^' aufgeteilt werden (Gl. 4):

$\sigma _{ij}^{\prime }={\begin{bmatrix}(\sigma _{xx}-p)&\tau _{xy}&\tau _{xz}\\\tau _{yz}&(\sigma _{yy}-p)&\tau _{yz}\\\tau _{zx}&\tau _{zy}&(\sigma _{zz}-p)\end{bmatrix}}$

(4)

In komplexeren Beanspruchungsfällen ist zur Beschreibung des Deformationszustandes eine exakte Analyse der relativen Verschiebungen benachbarter Massenpunkte notwendig. Im Ergebnis einer derartigen Analyse wird der Deformationszustand durch einen Verzerrungstensor $\epsilon _{ij}\!$ beschrieben, dessen Komponenten analog zum Spannungstensor (Gl. 5) in Form einer symmetrischen Matrix angeordnet werden:

$\epsilon _{ij}={\begin{bmatrix}\epsilon _{xx}&\gamma _{xy}&\gamma _{xz}\\\gamma _{yz}&\epsilon _{yy}&\gamma _{yz}\\\gamma _{zx}&\gamma _{zy}&\epsilon _{zz}\end{bmatrix}}$

(5)

Die relativen Längenänderungen des Systems bezüglich der Achsen x, y, z des Koordinatensystems werden durch die Dehnungen ε_xx, ε_yy und ε_zz beschrieben. Im Unterschied dazu kommen Winkeländerungen in den Scherkomponenten γ_xy, γ_yz und γ_zx zum Ausdruck. Der Verzerrungstensor weist formal ähnliche Eigenschaften wie der Spannungstensor auf. So kann ein Hauptachsensystem 1, 2, 3 angegeben werden, bezüglich dessen die Scherungen verschwinden und nur die Hauptdehnungen ε₁, ε₂ und ε₃ existieren. Weiterhin ist die Bestimmung von drei Invarianten sowie die Unterteilung in einen hydrostatischen Volumenänderungsanteil und einen deviatorischen Gestaltänderungsanteil möglich.

Das verallgemeinerte HOOKE`sche Gesetz

Der Zusammenhang zwischen den mechanischen Beanspruchungsgrößen Spannung und Deformation wird durch das Werkstoffverhalten bestimmt und durch konstitutive Gleichungen (Stoffgesetze) beschrieben. Er stellt sich in Abhängigkeit vom strukturellen Aufbau des betrachteten Werkstoffs sowie von den Beanspruchungsbedingungen als außerordentlich vielfältig dar. Allein im Bereich der Kunststoffe reicht das Spektrum von spröd-harten glasartig erstarrten amorphen Polymeren über duktile teilkristalline Thermoplaste und weich-elastische Gummiwerkstoffe bis zu flüssigkeitsähnlichen Polymerschmelzen. Wegen der Vielfalt der zu beobachtenden Phänomene ist eine einheitliche Beschreibung kaum möglich. Deshalb werden unter vereinfachenden Annahmen Grundtypen des mechanischen Verhaltens definiert, die eine näherungsweise Beschreibung des Spannungs-Dehnungs-Zusammenhanges (siehe Zugversuch) in engen Gültigkeitsgrenzen gestatten.
Für den allgemeinen Fall einer mehrachsigen Beanspruchung wird das energieelastische Verhalten durch das verallgemeinerte HOOKE’sche Gesetz beschrieben. Dieses basiert auf der Annahme, dass jede der sechs Komponenten des Spannungstensors σ_ij linear von den sechs Komponenten des Verformungstensors ε_kl abhängt:

$\sigma _{ij}=C_{ijkl}\cdot \epsilon _{kl}$

(6)

$\epsilon _{ij}=D_{ijkl}\cdot \sigma _{kl}$.

(7)

Die Proportionalitätskonstanten zwischen den Komponenten von Spannungs- und Verformungstensor bilden einen Tensor vierter Stufe der als Elastizitäts- oder Steifigkeitstensor C_ijkl bzw. als Nachgiebigkeitstensor D_ijkl bezeichnet wird. Dieser Tensor besteht aus 81 Komponenten, von denen im statischen Gleichgewicht jedoch lediglich 21 unabhängig voneinander sind. Symmetrieeigenschaften des Werkstoffs können zu einer weiteren Verringerung der Anzahl unabhängiger Komponenten führen. Für einen isotropen Werkstoff sind zwei Komponenten für eine vollständige Beschreibung des Elastizitäts- bzw. Nachgiebigkeitstensors erforderlich. Der Zusammenhang zwischen Spannungs- und Deformationszustand des isotropen Werkstoffs stellt sich damit in vektorieller Schreibweise wie folgt dar [1] (Gl. 8):

${\begin{Bmatrix}\sigma _{xx}\\\sigma _{yy}\\\sigma _{zz}\\\tau _{xy}\\\tau _{yz}\\\tau _{zx}\end{Bmatrix}}={\begin{bmatrix}C_{11}&C_{12}&C_{12}&0&0&0\\C_{12}&C_{11}&C_{12}&0&0&0\\C_{12}&C_{12}&C_{11}&0&0&0\\0&0&0&{\frac {C_{11}-C_{12}}{2}}&0&0\\0&0&0&0&{\frac {C_{11}-C_{12}}{2}}&0\\0&0&0&0&0&{\frac {C_{11}-C_{12}}{2}}\end{bmatrix}}\cdot {\begin{Bmatrix}\epsilon _{xx}\\\epsilon _{yy}\\\epsilon _{zz}\\\gamma _{xy}\\\gamma _{yz}\\\gamma _{zx}\end{Bmatrix}}$

(8)

Korrelation der elastischen Kenngrößen E, v, K und G

Die elastischen Konstanten C₁₁ und C₁₂ stehen mit dem Elastizitätsmodul E und der Querkontraktionszahl ν des isotropen Werkstoffs im Zusammenhang:

$E={\frac {\sigma _{2}-\sigma _{1}}{\epsilon _{2}-\epsilon _{1}}}={\frac {F_{2}-F_{1}}{0,002\ A_{0}}}$

(9)

$\mu _{b}=\left|{\frac {\epsilon _{qb}}{\epsilon }}\right|=\left|{\frac {\Delta b\ l_{0}}{\Delta l\ b_{0}}}\right|$.

(10)

Aus dem Elastizitätsmodul E und der Querkontraktionszahl ν können weitere Werkstoffkenngrößen wie der Schermodul G und der Kompressionsmodul K (siehe Energieelastizität) berechnet werden:

$G={\frac {\tau }{\gamma }}={\frac {E}{2(1+\nu )}}={\frac {C_{11}-C_{12}}{2}}$

(11)

$K={\frac {p}{\frac {\Delta V}{V_{0}}}}={\frac {E}{3(1-2\nu )}}={\frac {C_{11}+2C_{12}}{3}}$.

(12)

Literaturhinweis

[1]	Lüpke, T.: Grundlagen mechanischen Verhaltens. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 81–86 (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18)