Plastic-Hinge Modell
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Plastic-Hinge Modell (Türangelmodell)
Grundlagen
Das Plastic-Hinge Modell (Türangelmodell) stellt ein weit verbreitetes Modell zur Bestimmung der kritischen Rissöffnungsverschiebung für Dreipunktbiegeprüfkörper (SENB-Prüfkörper) dar [1].
Während bei quasistatischer Beanspruchung die kritische Rissöffnung durch optische Verfahren bzw. durch Messung der Kerbaufweitung v und Extrapolation auf die Rissspitze bestimmt werden kann, ist bei dynamischer Beanspruchung (siehe: Schlagbeanspruchung Kunststoffe) nur eine indirekte Ermittlung über die elektronisch gemessene Durchbiegung möglich. Von Zeislmair und Dahl werden in [2] zahlreiche Verfahren zur Bestimmung von Rissöffnungswerten bei statischer Beanspruchung, die überwiegend empirisch entwickelt wurden, zusammengestellt und die Ergebnisse miteinander verglichen. Voraussetzung für die Ermittlung der kritischen Rissöffnung bei dynamischer Beanspruchung ist, dass sich im Prüfkörper ein quasistatischer Spannungszustand (siehe: Ebener Spannungs- und Dehnungszustand) aufbaut, dessen Ausbildung durch die Einhaltung der Bedingung von Gl. (1)
| (1) |
mit
| tB | Bruchzeit | |
| τ | Periode der charakteristischen Trägheitsschwingung (siehe auch Aufschlagimpuls) |
kontrolliert wird.
Prinzip des Türangelmodells (Plastic-Hinge-Modell)
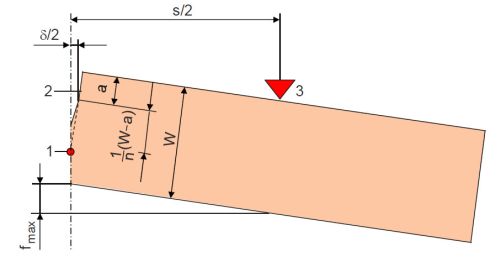
Vergleichende Untersuchungen zu verschiedenen Modellvorstellungen bei Biegebeanspruchung eines SENB-Prüfkörpers führen zu dem Ergebnis, die Ermittlung der kritischen Rissöffnung auf der Basis des „Plastic-Hinge“-Modells (Türangelmodell) durchzuführen [2−5]. Bei diesem Modell öffnen sich die Rissflanken unter zunehmender Prüflast, wie an einem Scharnier um einen als Rotationszentrum bezeichneten Punkt vor der Rissspitze, wobei auf Grund der Symmetrie des Prüfkörpers nur eine Hälfte der Probe betrachtet wurde (Bild 1).
| Bild 1: | Prinzip des Plastic-Hinge-Modells für SENB-Prüfkörper (1-Rotationszentrum, 2 scharfer Kerb, 3-Widerlager) [6] |
Die experimentell ermittelte Durchbiegung fmax setzt sich aus einem Anteil der durch die Biegung des ungekerbten Teils fB und dem durch die Deformation im Bereich des Kerbes hervorgerufenen Teils fK nach Gl. (2) zusammen,
| (2) |
wobei der Biegeanteil über die Beziehung
| (3) |
mit
| E | Elastizitätsmodul | |
| s | Stützweite | |
| B | Prüfkörperdicke | |
| W | Prüfkörperbreite |
errechnet wird.
Ermittlung der kritischen Rissöffnung
Für den biegebeanspruchten SENB-Prüfkörper gilt auf der Basis des Plastic-Hinge-Modells (Türangelmodells) (Bild 1) die Bestimmungsgleichung
| (4) |
Damit wird bei der Berechnung der kritischen Rissöffnung (siehe: Erweitertes CTOD-Konzept) die Betrachtung auf den Bereich an der Kerbspitze reduziert, indem der Anteil der Durchbiegung eines ungekerbten Prüfkörpers von der maximalen Durchbiegung fmax des gekerbten Prüfkörpers (entsprechend Gl. 2) subtrahiert wird.
Der Rotationsfaktor n ist, wie aus der Literatur [2, 7‒9] hervorgeht, von der Belastung abhängig und bewegt sich mit zunehmender Belastung auf die Rissspitze zu.
Der Rotationsfaktor n
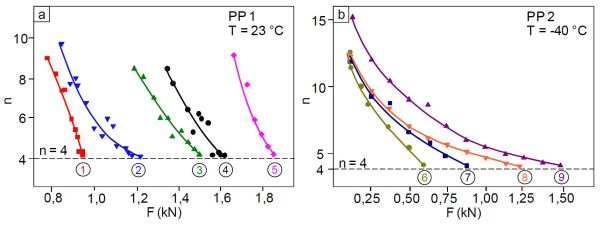
| Bild 2: | Abhängigkeit des Rotationsfaktors n von der Kraft für PP 1 a) (1 bis 5 ausgewählte Wärmebehandlungszustände) und PP 2 b) (6 bis 9 ausgewählte Orientierungsgrade) [7, 8] |
Für quasistatisch beanspruchte CT-Prüfkörper konnte durch die gleichzeitige Registrierung von Kerbaufweitung vc und Lastangriffspunktverschiebung vL für verschiedene Polymerwerkstoffe gezeigt werden, dass der Rotationsfaktor im Moment des Bruches den Grenzwert n = 4 annimmt (vgl. Bild 2) [6,10].
Einfluss des a/W-Verhältnisses
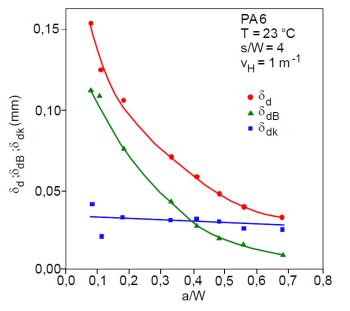
In Bild 3 wird die für einen Polyamidwerkstoff (Kurzzeichen: PA) mit elastischem Werkstoffverhalten nach Gl. (4) mit einem Rotationsfaktor n = 4 berechnete kritische Rissöffnung δdk im Vergleich zu δd und δdB in Abhängigkeit vom a/W-Verhältnis gezeigt.
| Bild 3: | Einfluss des a/W-Verhältnisses auf die kritischen Rissöffnungen δd, δdB und δdK bei instabiler Rissausbreitung für Polyamid |
Zur Berechnung von δd und δdB wird in Gl. (4) fK durch fmax bzw. fB ersetzt. Man erkennt unter Einbeziehung der in [1] dargestellten Ergebnisse für PE-HD+Hp und einen weiteren PP-Werkstoff PP 3, dass
- für die Bestimmung von kritischen Rissöffnungswerten bei kleinen a/W der Biegeanteil dominierend ist, wobei mit zunehmendem a/W δdB kleiner wird. Für Polyamid ist bei a/W = 0,1 δdB = 75 % und für a/W = 0,7 nur noch 25 %,
- der Anteil δdB für PP 3 bei s/W = 7 für hohe a/W vernachlässigbar klein wird,
- die aus dem Kerbanteil fK nach Gl. 4 ermittelten Rissöffnungen δdK unabhängig vom a/W-Verhältnis sind.
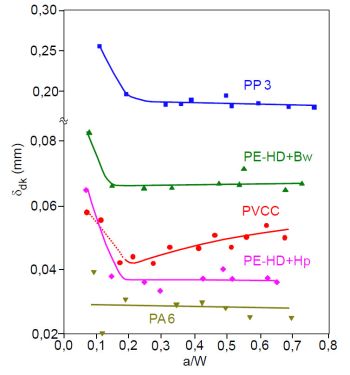
Die Unabhängigkeit von δdK vom a/W-Verhältnis wird in Bild 4 für ausgewählte Polymerwerkstoffe dargestellt.
| Bild 4: | Abhängigkeit der kritischen Rissöffnungen δdK vom a/W-Verhältnis für PP 3 (vH = 1,5 ms-1; s/W = 7), PE-HD+Bw (vH = 1,5 ms-1; s/W = 4), PVCC (vH = 1 ms-1; s/W = 4), PE-HD+Hp (vH = 1,5 ms-1; s/W = 4) und PA (vH = 1 ms-1; s/W = 4) |
Der für a/W < 0,2 ersichtliche Anstieg in den δdK-Werten beruht auf der für die niedrigsten a/W-Verhältnisse sehr hohen Energieaufnahme der Prüfkörper beim Schlagvorgang (siehe: Schlagbeanspruchung Kunststoffe), so dass die empirische Bedingung zur Kontrolle der Energieaufnahme beim Schlagvorgang (siehe: IKBV Experimentelle Bedingungen), wonach die vom Pendelkammer für den Bruchvorgang angegebenen Schlagenergie AH größer als das 3-fache der von dem Prüfkörper verbrauchten Verformungsenergie AG sein muss, für alle Werkstoffe nicht mit ausreichender Sicherheit erfüllbar ist und für PVCC erst ab a/W ≤ 0,17, weshalb der Verlauf in Bild 4 nur gestrichelt gekennzeichnet wurde.
Aus der Bildunterschrift zu Bild 4 werden die für die verschiedenen Polymerwerkstoffe unter dem Aspekt der Einhaltung der experimentellen Bedingungen des instrumentierten Kerbschlagbiegeversuches gewählten Beanspruchungsbedingungen deutlich, die zu unterschiedlichen Deformationsgeschwindigkeiten an der Rissspitze führen. Als Maß zu deren Beschreibung kann die Rissöffnungsgeschwindigkeit Gl. (5)
| (5) |
herangezogen werden. Die Bruchzeit tB wird nach Gl. (6)
| (6) |
berechnet. Δv kennzeichnet die Änderung der Pendelhammergeschwindigkeit während des Verformungsvorganges, die nach Gl. (7) um so größer zu erwarten ist, je höher die Verformungsenergie AG des Prüfkörpers und die Pendelhammergeschwindigkeit vH vor dem Schlag ist:
| (7) |
mH = Masse des Pendelhammers, die durch Wägen in waagerechter Lage ermittelt wird [11].
Rissöffnungsgeschwindigkeit ausgewählter Kunststoffe
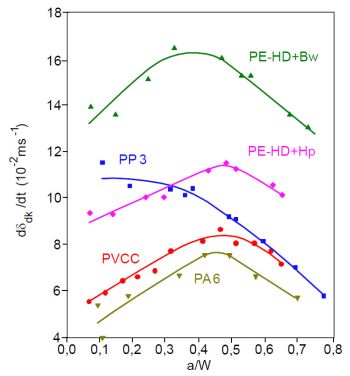
In Bild 5 werden die aus Gl. (5) ermittelten Rissöffnungsgeschwindigkeiten in Abhängigkeit vom a/W-Verhältnis dargestellt. Die mit Ausnahme von PP 3 festgestellten Zunahmen von dδdK/dt bis etwa a/W = 0,5 resultieren vorwiegend aus der Abnahme von fmax mit zunehmendem a/W und die Abnahme von dδdK/dt für a/W > 0,5 daraus, dass fmax bei gleichzeitiger kontinuierlicher Verringerung von Δv wieder ansteigt.
| Bild 5: | Rissöffnungsgeschwindigkeiten dδdK/dt für verschiedene Kunststoffe |
Die Abhängigkeit von dδdK/dt vom a/W-Verhältnis für PP 3 deutet darauf hin, dass für s/W = 7 die Beanspruchung des Werkstoffes im Rissspitzenbereich vergleichbar mit dem anderer Kunststoffe ist, wobei sich neben den hohen Bruchzeiten (hier muss der Einfluss des Durchziehens der Prüfkörper durch die Widerlager berücksichtigt werden) der niedrige Biegeanteil δdB auswirkt und somit dem Kerbanteil bei s/W = 7 auch für kleine a/W bereits die entscheidende Bedeutung zukommt.
Bei Berücksichtigung des Durchziehens der Prüfkörper durch die Widerlager (siehe: Auflagerabstand) wird die dδdK/dt-Kurve zu höheren Werten verschoben.
Die Rissöffnungsgeschwindigkeit dδ/dt bietet gleichzeitig die Möglichkeit, die für verschiedene Prüfkörpergeometrien entstehenden unterschiedlichen Beanspruchungsbedingungen auf eine prüfkörperinvariante Deformationsgeschwindigkeit an der Rissspitze umzurechnen und diese als Parameter bei werkstoffspezifischen Untersuchungen heranzuziehen.
Literaturhinweise
| [1] | Grellmann, W.: Beurteilung der Zähigkeitseigenschaften von Polymerwerkstoffen durch bruchmechanische Kennwerte. Habilitation (1986), Technische Hochschule Merseburg, Wiss. Zeitschrift TH Merseburg 28 (1986), H. 6, S. 787‒788 (Inhaltsverzeichnis, Kurzfassung) |
| [2] | Schwalbe, K. H.: Fortschritts-Berichte VDI-Z. Reihe 18, Nr. 10, VDI-Verlag, 1981 |
| [3] | Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig (1982), (ISBN: VLN 152-915/62/73; siehe AMK-Büchersammlung unter E 29-1) |
| [4] | Kobayashi, T.: Eng. Fracture Mechanics 19 (1984) 67 |
| [5] | Schwalbe, K.-H.: Bruchmechanik metallischer Werkstoffe. Carl Hanser Verlag, München Wien (1980), (ISBN: 3-446-12983-9; siehe AMK-Büchersammlung unter E 15) |
| [6] | Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 254‒255, (ISBN 978-446-44300-1; siehe AMK-Büchersammlung unter A 18) |
| [7] | Hille, E.: Untersuchungen zum Bruchverhalten des orientierten isotaktischen Polypropylen. Dissertation, TH Leuna-Merseburg, 1983 |
| [8] | Newe, R.: Untersuchungen zum Bruchverhalten des nichtorientierten isotaktischen PP. Dissertation, TH Leuna-Merseburg, 1980 |
| [9] | Hollstein, T., Blauel, J. G., Wenk, K.: 12. Sitzung des Arbeitskreises Bruchvorgänge im DVM Freiburg, 7./8.10.1980 |
| [10] | Jungbluth, M.: Untersuchungen zum Verformungs- und Bruchverhalten von PVC-Werkstoffen. Dissertation, TH Leuna-Merseburg (1987) (siehe AMK-Büchersammlung unter B 1-1) |
| [11] | DIN EN ISO 13802 (2016-07): Kunststoffe ‒ Verifizierung von Pendelschlagwerken – Charpy-, Izod- und Schlagzugversuch |