Probennachgiebigkeit
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Probennachgiebigkeit oder auch Prüfkörpernachgiebigkeit
siehe auch: Steifigkeit, Maschinennachgiebigkeit und Druckversuch Nachgiebigkeit
Allgemeines
Bei dem Begriff Nachgiebigkeit unterscheidet man in der Werkstoff- oder Kunststoffprüfung zwei grundlegende Einflussgrößen auf die Ermittlung von Kennwerten. Dies ist einmal die sogenannte Maschinensteifigkeit als Eigenschaft einer Materialprüfmaschine und die Steifigkeit des Prüfkörpers, die auch als Probensteifigkeit oder Prüfkörpersteifigkeit bezeichnet wird.
In Abhängigkeit von der Art des Versuches der Werkstoffprüfung (Zug-, Druck- oder Biegeversuch) und der absoluten Belastungshöhe muss die Universalprüfmaschine einen hinreichenden Widerstand gegen die unvermeidbare Eigenverformung des Lastrahmens und der Kraftmesszelle (siehe Elektro-Mechanischer Kraftaufnehmer und Piezoelektrischer Kraftaufnehmer) aufweisen. Die Zug- oder Drucknachgiebigkeit der Prüfmaschine mit identischer Kraftmessdose kann in Vernachlässigung der Einspann- und Verlängerungselemente als nahezu gleich angesetzt werden. Im Biegeversuch ist der Einfluss der Maschinennachgiebigkeit unabhängig von der Verfahrrichtung der Traverse nahezu vernachlässigbar, da die Kräfte in diesem Versuch deutlich geringer als im Druck- oder Zugversuch sind. Ein besonderer Fall liegt vor, wenn Torsionsversuche (siehe: Dynamisch-Mechanische Analyse (DMA) – Torsionsbeanspruchung) durchgeführt werden, da dann eine andere Belastungsart und Nachgiebigkeit der speziellen Materialprüfmaschine vorliegt.
Unabhängig von der Art des Versuches tritt ein Widerstand des Prüfkörpers gegen die erzwungene Verformung auf, der als Probennachgiebigkeit bezeichnet wird. Maschinen- und Probensteifigkeit müssen in einer ausgewogenen Relation zueinander stehen, um Einflüsse auf die Kennwertermittlung und die Regelung der Prüfmaschinen (siehe: Zugversuch Regelung) zu vermeiden.
Maschinensteifigkeit
Unter der Maschinennachgiebigkeit oder Nachgiebigkeit (Compliance) C versteht man in der Werkstoffprüfung die Eigendeformation des geschlossenen Lastrahmens von Universalprüfmaschinen mit zwei oder vier Rahmensäulen [1, 2] oder die Aufweitung des Lastgestells z. B. von Härteprüfmaschinen [3, 4] oder Prüfmaschinen mit einer zentralen Antriebsspindel.
Wird eine Universalprüfmaschine zur Durchführung von Zugversuchen, Druckversuchen (siehe auch Druckprüfanordnung) und Biegeversuchen eingesetzt, dann entsteht neben der Verformung des Prüfkörpers eine Deformation der Prüfmaschine, die von der Steifigkeit der Konstruktion, den verwendeten Werkstoffen, der genutzten Kraftmessdose und den Anschluss- sowie Verbindungselementen maßgeblich abhängt. Die unterschiedlichen Deformationsanteile einer Prüfmaschine bestehen aus der Eigenverformung der nicht unendlich steifen Prüfmaschine. Dies sind die Biegung des Querhaupts und der Traverse sowie die Verlängerung der tragenden Lastsäulen und der Antriebsspindel (siehe: Antriebe für Materialprüfmaschinen), deren Absolutbetrag jedoch vergleichsweise gering ist. In Abhängigkeit von der Nennkapazität der Kraftmessdose sind ebenfalls Deformationen des elastischen Deformationskörpers im Gesamtmesssignal enthalten. Da die Verbindungsgestänge erfahrungsgemäß immer etwas Spiel aufweisen, entstehen zusätzliche Verformungen, die insbesondere von der Anzahl der Verbindungselemente und deren konstruktiven Ausführung abhängen. Den größten Einfluss üben jedoch die Einspannelemente aus, wobei hier je nach Bauart der Klemmeinrichtung deutliche Unterschiede auftreten. Im Fall des Zugversuches weisen Keilspannzeuge die größten Fehlwege und nachspannende Parallelspannklemmen die geringsten Deformationen auf. Bei der Druck- und Biegeprüfung ist der Einfluss der Auflagerelemente wesentlich geringer. Grundsätzlich ist die Maschinennachgiebigkeit ohne das spezifische Versuchszubehör um Größenordnungen höher als im konkreten Versuch der Werkstoff- oder Kunststoffprüfung.
Probensteifigkeit
Unter der Steifigkeit eines Werkstoffes wird im Regelfall der Elastizitäts- oder Schubmodul (Schermodul) für die jeweilige Beanspruchungsart im linear-elastischen Beanspruchungsbereich verstanden. Für den Zugversuch ist das der E-Modul Et, im Druckversuch Ec und im Biegeversuch wird der Biege-E-Modul Ef verwendet, während im Torsions- oder Scherversuch der Gleit- oder Schubmodul G zur Anwendung kommt. Für größere Deformationen wird nicht mehr der Elastizitätsmodul, sondern oftmals der Anstieg z. B. der Spannungs-Dehnungs-Kurve dσ/dε (siehe: Zugversuch) zur Beschreibung der Steifigkeit bei einer vorgegebenen Verformung benutzt.
Die Steifigkeit eines Bauteils gegenüber einem konkreten Belastungsfall wird durch die Dimensionierung (z. B. Wanddicke oder Außendurchmesser) und die konstruktive Auslegung (z. B. geometrische Gestaltung, offene oder geschlossene Profile oder Verrippungen) bestimmt. Aufgrund unterschiedlicher geometrische Parameter wird die Steifigkeit eines Bauteils bzw. dessen Widerstand gegenüber einer Verformung bei differierenden Beanspruchungen nur in Ausnahmefällen übereinstimmen, weshalb komplexe Belastungen (z. B. Zug, Biegung und Torsion) selbst ohne schwingende oder schlagartige Lasten eine Herausforderung darstellen.
Die Probensteifigkeit S in der Werkstoffprüfung stellt im Regelfall das Produkt aus Steifigkeit des Werkstoffes und einer speziellen geometrischen Größe dar. Aufgrund der Anforderungen der Werkstoffprüfung und der für die Versuche optimierten Prüfkörperform werden somit unterschiedliche Probensteifigkeiten genutzt.
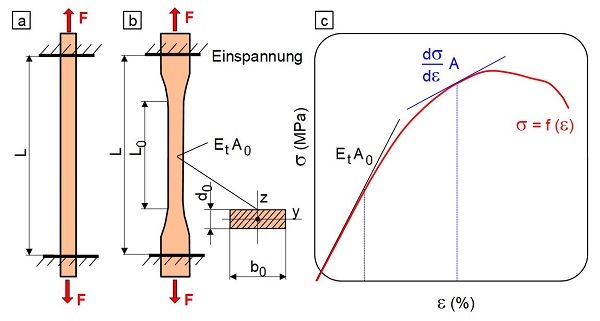
| Bild 1: | Schematischer Erläuterung zur Probennachgiebigkeit im Zugversuch |
Im Zugversuch werden in der Kunststoffprüfung teilweise prismatische [5] oder Vielzweckprüfkörper des Typs 1A oder 1B genutzt [6], wobei die letzteren zur besseren Klemmbarkeit Schultern auf beiden Seiten besitzen (Bild 1). Bei dem prismatischen Prüfkörper ist die Probensteifigkeit St innerhalb der Einspannlänge L konstant und berechnet sich nach der Gl. (1) für eine linear-elastische Deformation. Diese Gleichung gilt ebenfalls für den Schulterprüfkörper, allerdings nur im planparallelen Teil des Prüfkörpers (Bild 1a und b).
| (1) |
Überschreitet die Dehnung im Zugversuch den linear-viskoelastischen Bereich, dann treten erste Mikroschädigungen auf, die Spannungs-Dehnungs-Kurve krümmt sich und der Prüfkörperquerschnitt nimmt entsprechend der Poissonzahl des jeweiligen Werkstoffes ab.
Aufgrund dessen muss zur Beschreibung der aktuellen Probensteifigkeit die Gl. (2) verwendet werden, die immer nur für die momentane Dehnung des Prüfkörpers gültig ist (Bild 1c).
| (2) |
Die Probennachgiebigkeit im Zugversuch Ct ergibt sich als Kehrwert der Probensteifigkeit St nach Gl. (3) und wird in der Maßeinheit 1/N angegeben. Mit zunehmenden Prüfkörperquerschnitt und/oder ansteigendem E-Modul Et verringert sich die Probennachgiebigkeit.
| (3) |
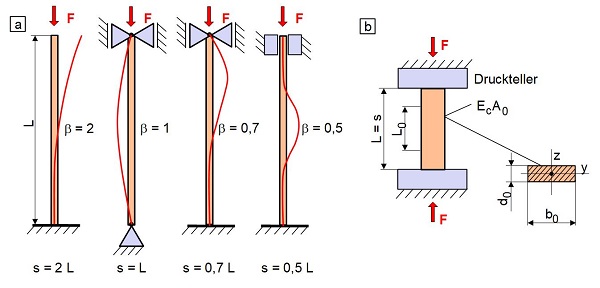
Die Probensteifigkeit im Druckversuch berechnet sich analog zum Zugversuch, allerdings ergeben sich in Abhängigkeit von der Prüfkörperlänge, dem Querschnitt und den Lagerungsbedingungen des Prüfkörpers unterschiedliche Beanspruchungsfälle. Bei sehr langen, schlanken Prüfkörpern tritt ein spezieller Versagensfall auf, der auch als EULER’ sches Knicken bezeichnet wird (Bild 2a) und ein Instabilitätsproblem darstellt [7]. In Abhängigkeit von den Lagerungsbedingungen, der Geometrie und dem E-Modul des Prüfkörpers kann infolge einer Druckbeanspruchung bei einer kritischen Last ein seitliches Ausknicken (Biegeknicken) auftreten. Bei Torsion oder Biegung mit Torsion können dagegen Drill- oder Biegedrillknicken (Kippen) zum Versagen führen. Im elastischen Deformationsbereich wird die kritische Knicklast oder Druckbeanspruchung Fk nach der Gl. (4) berechnet und die Knickspannung σk ergibt sich nach Gl. (5).
| (4) |
| (5) |
In der Gl. (4) ist Ec der E-Modul bei Druckbeanspruchung, Iy das minimale axiale Flächenträgheitsmoment und s die sogenannte Knicklänge, die das Produkt aus dem Knicklängenbeiwert β und der Prüfkörperlänge L ist (s = β L). Der Wert λ wird als Schlankheitsgrad bezeichnet und ergibt sich nach Gl. (6), wobei iy der sogenannte minimale Trägheitsradius nach Gl. (7) ist.
| (6) |
| (7) |
| Bild 2: | Knickverhalten und Probennachgiebigkeit im Druckversuch |
Die Auflagerverhältnisse im Druckversuch (Bild 2b) entsprechen dem zweiten elastischen Knickfall in Bild 2a, wodurch gilt s = L. Um zu verhindern, dass ein Ausknicken der Prüfkörper im Druckversuch auftritt, soll der Schlankheitsgrad λ = 6 bis 10 betragen, weshalb sich die Länge L eines prismatischen Prüfkörpers nach Gl. (8) berechnet [8].
| (8) |
Bei dem prismatischen Prüfkörper ist die Probensteifigkeit Sc innerhalb der Einspannlänge L konstant und berechnet sich nach der Gl. (9) für eine linear-elastische Deformation.
| (9) |
Überschreitet die Stauchung im Druckversuch den linear-viskoelastischen Bereich, dann treten Mikroschädigungen auf und die Spannungs-Stauchungs-Kurve wird zunehmend nichtlinear weshalb dann zur Beschreibung der aktuellen Probensteifigkeit die Gl. (10), die für die momentane Stauchung des Prüfkörpers gültig ist, zu verwenden ist (siehe Bild 1c).
| (10) |
In Analogie zum Zugversuch ergibt sich die Probennachgiebigkeit Cc im Druckversuch ebenfalls als Kehrwert der Probensteifigkeit Sc nach Gl. (11) und wird in der Maßeinheit 1/N angegeben.
| (11) |
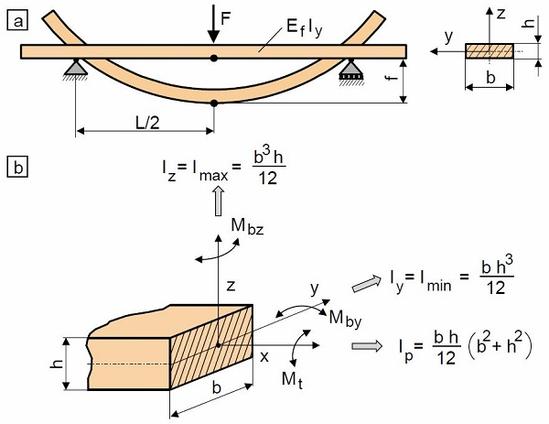
| Bild 3: | Probennachgiebigkeit im Biege- und Torsionsversuch |
Im Biegeversuch ist die steifigkeitsbeschreibende Geometriegröße das axiale Flächenträgheitsmoment, unabhängig davon, ob Drei- oder Vierpunktbiegung (siehe: Biegeversuch) vorliegt. Dabei ist jedoch von Bedeutung, ob die Biegung um die y- oder z-Achse, wie z. B. in Schlagbiegeversuchen üblich, erfolgt. In diesen Fällen muss dann das minimale oder maximale axiale Flächenträgheitsmoment Iy oder Iz verwendet werden (Bild 3a). In der Regel erfolgt im Dreipunktbiegeversuch an Kunststoffen [9] die Biegung um die y-Achse des prismatischen Prüfkörpers, so dass sich die Probensteifigkeit nach der Gl. (12) berechnet.
| (12) |
Bei einer nichtlinearen Biegespannungs-Randfaserdehnungs-Kurve (siehe: Biegebeanspruchung) wird zur Beschreibung der aktuellen Probensteifigkeit die Gl. (13) verwendet ist (siehe Bild 1c).
| (13) |
In Analogie zum Zugversuch ergibt sich die Probennachgiebigkeit Cf im Biegeversuch auch als reziproker Wert der Probensteifigkeit Sf nach Gl. (14) und wird in der Maßeinheit 1/N mm2 angegeben.
| (14) |
Bei dem Torsionsversuch ergibt sich die Probensteifigkeit eines prismatischen Prüfkörpers als Produkt aus dem Schub- oder Gleitmodul G und dem polaren Flächenträgheitsmoment Ip (Bild 3b) nach Gl. (15).
| (15) |
Die Probennachgiebigkeit Cto im Torsionsversuch ist auch als reziproker Wert der Probensteifigkeit Sto nach Gl. (16) definiert und hat die Maßeinheit 1/N mm2.
| (16) |
Die Probennachgiebigkeit des jeweiligen Versuchs setzt die Abwesenheit von Kerben und Kerbspannungen voraus. Bei geometrisch komplizierten Prüfkörperformen, z. B. wie CT-Prüfkörpern ist schon infolge der komplexen Beanspruchung die Angabe von Nachgiebigkeitswerten äußert schwierig, so dass hier in der Regel numerische Lösungsvarianten eingesetzt werden.
Literaturhinweise
| [1] | Heimbrodt, P.: Einfluss der Prüfmaschine auf die Kennwerte des Zugversuches. Bergakademie Freiberg, Diplomarbeit (1976) |
| [2] | Instron Bluehill: Referenzhandbuch – Software für Berechnungen Rev. 1.1 (2006) |
| [3] | Reimann, E.: Bestimmung mechanischer Werkstoffkennwerte, Ergebnisse des instrumentierten Eindringversuchs im Makrobereich. Materialprüfung 42 (2000) 10, S. 411–415 |
| [4] | Zügner, S.: Untersuchungen zum elastisch-plastischen Verhalten von Kristalloberflächen mittels Kraft-Eindringtiefen-Verfahren. Dissertation, Bayerische Julius-Maximilians-Universität Würzburg (2002) |
| [5] | DIN EN ISO 527-5 (2022-05): Kunststoffe – Bestimmung der Zugeigenschaften – Teil 5: Prüfbedingungen für unidirektional faserverstärkte Kunststoffverbundwerkstoffe |
| [6] | DIN EN ISO 527-2 (2012-06): Kunststoffe – Bestimmung der Zugeigenschaften – Teil 2: Prüfbedingen für Form- und Extrusionsmassen |
| [7] | Szabo, I.: Einführung in die Technische Mechanik. Springer Verlag, Berlin (1984) 8. Auflage, (ISBN 3-540-13293-7; siehe AMK-Büchersammlung unter T 15) |
| [8] | Bierögel, C.: Quasistatische Prüfverfahren. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 111–157 (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18) |
| [9] | DIN EN ISO 178 (2019-08): Kunststoffe – Bestimmung der Biegeeigenschaften |