Rissmodell nach IRWIN und Mc CLINTOCK

Ein Service der
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung
PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Rissmodell nach IRWIN und Mc CLINTOCK

Grundlagen des Modells

Die Anwendung des Rissmodells nach GRIFFITH und die sich darauf aufbauende Bestimmung der Bruchzähigkeitskennwerte sind an eine rein elastische Deformation des beanspruchten Werkstoffes gebunden.

Die meisten technischen Werkstoffe weisen jedoch auch beim Auftreten eines makroskopisch spröd erscheinenden Bruchs plastische Verformungen im mikroskopischen Bereich auf.

Um die Anwendbarkeit der LEBM zu gewährleisten, müssen die plastischen Deformationen an der Rissspitze klein im Vergleich zur Risslänge und den Bauteilabmessungen sein.

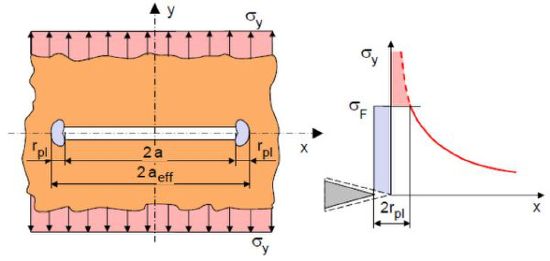
Bild 1:

Rissmodell nach IRWIN und Mc CLINTOCK

Nach dem von Irwin und Mc Clintock aufgestellten Modell [1–3] wird davon ausgegangen, dass die zur Berechnung der Bruchzähigkeit notwendige Risslänge sich als Effektivwert a_eff (experimentelle Bestimmung siehe Effektive Risslänge) aus der Anfangsrisslänge a₀ und dem Radius der plastischen Zone a_pl (a_pl = r_pl) zusammensetzt.

$a_{eff}=a_{0}+a_{pl}$

Linear-elastische Bruchmechanik mit Kleinbereichsfließen

Das auf dem Rissmodell von IRWIN und Mc CLINTOCK aufbauende Bruchmechanikkonzept wird unter dem grundlegenden Begriff Bruchmechanik erläutert und als Linear-elastische Bruchmechanik mit Kleinbereichsfließen bezeichnet.

Die Größe der plastischen Zone a_pl lässt sich in einfacher Weise abschätzen, wenn man in den SNEDDON-WILLIAMS-Gleichungen die Spannungskomponenten durch die Streckgrenze R_e (R_e = σ_F) ersetzt.

Für Θ = 0 erhält man:

$r_{pl}=a_{pl}={\frac {1}{2\pi }}({\frac {K_{I}}{R_{e}}})^{2}$

für den ebenen Spannungszustand (ESZ) und

$r_{pl}=a_{pl}={\frac {1}{2\pi }}({\frac {K_{I}}{R_{e}}})^{2}(1-2\upsilon )^{2}$

für den ebenen Dehnungszustand (EDZ).

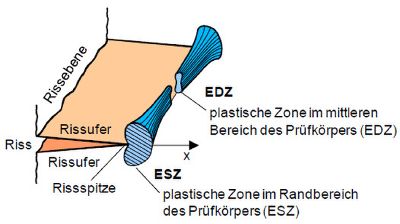
Durch die wachsende Verformungsbehinderung zur Probenmitte hin geht der am Rand der Probe herrschende ESZ in den EDZ über.
Die plastische Zone ist in der Probenmitte kleiner, es kommt somit zur Ausbildung der sog. „Hundeknochenform“ (dog bone model).

Bild 2:

Plastische Zone vor der Rissspitze entlang der Probenkörperbreite

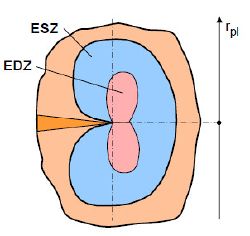
Bild 3:

Form der plastischen Zone vor der Rissspitze entlang der Probenkörperbreite

Der Spannungsintensitätsfaktor (siehe: Bruchmechanik) ergibt sich in diesem Fall nach

$K_{I}=\sigma (\pi a_{eff})^{\frac {1}{2}}f(a_{eff}|W)$

Die Anwendung dieser Modellvorstellung beschränkt sich auf den Fall

${\frac {R_{m}}{R_{e}}}<0,6$

Verhältnis von Zugfestigkeit zur Streckgrenze

Ist diese Bedingung nicht erfüllt und treten größere plastisch deformierte Bereiche auf, dann sind die Methoden der Fließbruchmechanik anzuwenden.
Dreidimensionale FEM-Rechnungen unter Berücksichtigung des Verfestigungsverhaltens haben gezeigt, dass die tatsächliche Form von diesen Modellvorstellungen abweicht.

Ausbildung der plastischen Zone für Kunststoffe

Da der experimentelle Nachweis sehr aufwendig ist, gibt es nur wenig Befunde in der Literatur [4].

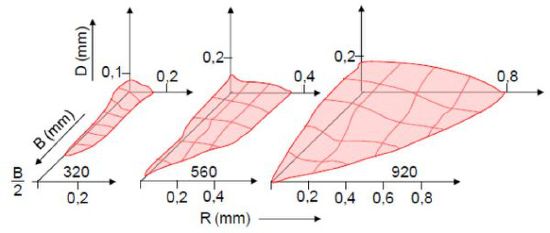
In Bild 4 ist ein Beispiel für eine plastische Zone in einem isotaktischen Polypropylen (Kurzzeichen: PP) dargestellt.

Bild 4:

Beispiel: Plastische Zone in Polypropylen [4]

Die wichtigsten Anwendungen einer sinngemäßen korrigierten Anwendung der Bruchmechanik auf Kunststoffe liegen heute in der Frage der strukturbedingten Realisierung der plastischen Zone. Eine Antwort auf diese Frage hängt naturgemäß von der speziellen Mikrostruktur des Kunststoffes ab.

Literaturhinweise

[1]	Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig Stuttgart (1982) S. 20 (siehe AMK-Büchersammlung unter E 29-1)
[2]	Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig (1987) 2. Auflage S. 20 (ISBN 3-342-00096-1; siehe AMK-Büchersammlung unter E 29-2)
[3]	Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig Stuttgart (1993) 3. Auflage, S. 17 (ISBN 3-342-00659-5; siehe AMK-Büchersammlung unter E 29-3)
[4]	Hoffmann, H., Grellmann, W., Hille, E., Newe, R.: Ermittlung und Anwendung bruchmechanischer Kennwerte zur Beschreibung der Zähigkeitseigenschaften von isotaktischem Polypropylen. Plaste und Kautschuk 29 (1982), H. 4, S. 230–237)