Schubmodul
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Schubmodul
Allgemeines
Der Schub- oder Schermodul G, auch als Gleit- oder Torsionsmodul bezeichnet, ist auch bei Kunststoffen neben der Poissonzahl eine wesentliche Kenngröße zur Beschreibung der energieelastischen Eigenschaften.
Die in quasistatischen Prüfungen wie dem Torsions- oder dem ein- bzw. zweischnittigem Scherversuch ermittelten Kurzzeitmoduli G sind für die Qualitätssicherung, die Werkstoffentwicklung und -optimierung als auch einfache Dimensionierungsaufgaben (siehe Kunststoffbauteil Dimensionierung) geeignet, aber nicht für anspruchsvolle konstruktive Anwendungen nutzbar, da in diesem Fall der Kriechmodul aus Langzeitexperimenten, auch in Abhängigkeit von der Prüftemperatur, bekannt sein muss.
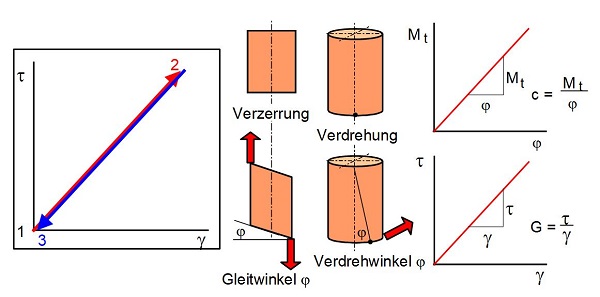
Die strukturelle Ursache des energieelastischen Verhaltens von Kunststoffen ist die Veränderung (Dehnung, Stauchung und Verzerrung) der mittleren Atomabstände und Bindungswinkel bei Einwirkung mechanischer Beanspruchungen. Die dabei geleistete mechanische Arbeit wird in Form potentieller Energie gespeichert (Zunahme der inneren Energie) und bei Aufhebung der Beanspruchung vollständig zurückgegeben (1. Hauptsatz der Thermodynamik). Infolge seiner strukturellen Ursachen ist das energieelastische Verhalten also auf den Bereich sehr kleiner Verformungen beschränkt. Es besteht eine völlige Reversibilität der Deformation (Scherung, Gleitung oder Schiebung), wobei der Zusammenhang zwischen Beanspruchung und Deformation linear oder nichtlinear sein kann (siehe: Elastizität). Die Be- und Entlastungkurve ist in jedem Fall identisch, wodurch keine Hysterese entsteht. Wird ein linearer Zusammenhang zwischen Spannung (Kraft oder Moment) und Gleitung oder Scherung (Deformation) beobachtet, dann kann der Zusammenhang im Fall einer Torsions- oder Scherbelastung in Analogie zu einer Feder- oder Proportionalitätskonstante durch das HOOKE´sche Gesetz für Schub oder Scherung (Gl. 1) für kleine Auslenkungs- oder Gleitungswinkel mit tan γ ≈ γ eindeutig beschrieben werden (Bild 1).
| Bild 1: | Elastische Deformation des Federmodells und des Festkörpers nach HOOKE |
| (1) |
Die Energieelastizität dominiert das Verhalten von Polymerwerkstoffen insbesondere bei kleinen Verformungen und bei tiefen Temperaturen sowie bei hohen Beanspruchungsgeschwindigkeiten (Dehnraten), wobei die klassische Energieelastizitätstheorie hier wesentlich zum Verständnis des Deformationsverhaltens der Kunststoffe beiträgt. Darüber hinaus liefert sie in diesem Bereich brauchbare Näherungslösungen für die quantitative Beschreibung des Spannungs-Dehnungs-Zusammenhanges einer Schub- oder Scherbeanspruchung [1].
In der prüftechnischen Praxis werden im Wesentlichen drei Methoden zur Ermittlung des Schub- oder Schermoduls angewandt. Dies sind die quasistatischen Versuche der Werkstoff- und Kunststoffprüfung, die dynamisch-mechanische Analyse und die Ultraschallprüfung, wobei die mechanischen Kurzzeitversuche (siehe: Zugversuch) die höchste Praxisrelevanz besitzen.
Quasistatische Kurzzeitversuche
Zur Ermittlung des Schubmoduls G werden in der quasistatischen Werkstoff- und Kunststoffprüfung der Torsions- und der Scherversuch unter Nutzung von Universalprüfmaschinen angewandt.
| Bild 2: | Torsionsprüfung: (a) – Schematisches Messprinzip, (b) Torsionsprüfmaschine TL1000 und hybride Universalprüfmaschine der Fa. ZwickRoell GmbH & Co. KG, Ulm |
In Bild 2a ist das Messprinzip zur Ermittlung des Schubmoduls im quasistatischen Torsionsversuch schematisch dargestellt. Der runde Prüfkörper ist am oberen Ende fest eingespannt und wird über eine zylindrische Scheibe durch zwei symmetrische Kräfte um den Winkel φ verdreht, wodurch das Torsionsmoment Mt = R · F als Belastung aufgebracht wird. Für sehr kleine reversible Verdrehwinkel ergibt sich dann der Schubmodul G nach der Gl. (2) aus den geometrischen Bedingungen und den Messgrößen F und φ.
| (2) |
| mit: | L | – | Prüfkörperlänge |
| R | – | Radius der Scheibe | |
| r | – | Prüfkörperradius |
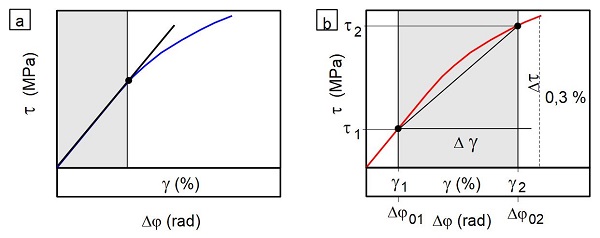
Im Gegensatz zur Prüfung unter Zug-, Druck- oder Biegebeanspruchung existieren für die quasistatische Torsionsprüfung nur sehr wenige Normen. Für die Torsions- oder Verwindungsprüfung von Drähten [2, 3] oder von Baustoffen aus Hölzern [4, 5] liegen verbindliche Standards vor oder für die Rohrprüfung von metallischen Werkstoffen werden Empfehlungen für Torsionsversuche gegeben, die zumeist aber nicht die Ermittlung des Schubmoduls beinhalten. Bei Kunststoffen sind diesbezüglich keine Normen verfügbar, da die Herstellung von Rundprüfkörpern schon aufgrund der Entformungsnähte erhebliche Probleme bereitet. Wird in Ermanglung entsprechender Prüfnormen der Schubmodul unter Torsionsbeanspruchung mit Prüfmaschinen nach den Bildern 2b oder 2c an prismatischen Kunststoffprüfkörpern vorgenommen werden, dann sollten analoge Regelungen wie bei der Ermittlung des E-Moduls im Zug- oder Biegeversuch beachtet werden. Aufgrund der vergleichsweise geringen elastischen Deformationen von < 0,1 % Dehnung und dem linear-viskoelastischen Verhalten, welches bis etwa 0,3 % registriert wird, können nur sehr kleine Kräfte und Verformungen genutzt werden. Die Verdrehung des Prüfkörpers sollte dabei 0,5 % nicht überschreiten, da dann möglicherweise nichtlinear-viskoelastische Deformationsanteile (siehe: Elastizität) wirken und die Deformationsgeschwindigkeit ist auf ca. 1 %/min zu begrenzen. Je nach dem Habitus des Torsionsspannungs-Schiebungs-Diagramms kann dann der Schubmodul als Tangentenmodul oder Sekantenmodul in den Deformationsgrenzen von etwa 0,05 und 0,25 % angegeben werden (Bild 3). Der Versuch sollte bei Verdrehungen > 0,3 % abgebrochen werden.
Der Schubmodul G wird dann für den Tangentenmodul nach Gl. (5) oder für den Sekantenmodul unter Nutzung von Δτ und Δγ nach Gl. (6) berechnet, wobei die Verdrehungen γ1 und γ2 als Vorgabewerte zur Ermittlung von τ1 und τ2 benutzt werden.
| Bild 3: | Ermittlung des Tangentenmoduls (a) und des Sekantenmoduls (b) im Torsions- und Scherversuch an Kunststoffen |
Zu beachten ist bei der Berechnung der Schubspannungen, dass im Fall des prismatischen Prüfkörpers das polare Flächenträgheitsmoment Ip des Kreisquerschnitts nach Gl. (3) nicht verwendet werden darf. Da die rechteckigen Querschnitte nicht wölbkraftfrei sind, ist Ip dann eine Näherung nach Gl. (4) [6].
| (3) |
| (4) |
| (5) |
| (6) |
Bei Bedarf können diese Versuche auch in einer Temperierkammer durchgeführt werden, wodurch der Schubmodul G als Funktion der Temperatur darstellbar ist.
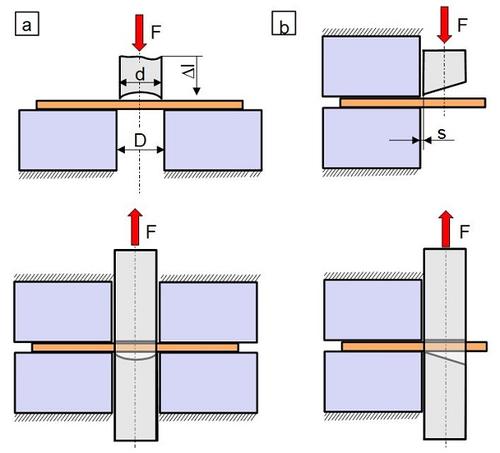
Bei dem Scherversuch existieren im Wesentlichen zwei technisch genutzte Varianten, die als ein- und zweischnittige Scherung bezeichnet werden [7] (Bild 4). Bedeutung besitzen diese Versuche nur für metallische Werkstoffe und Holzbaustoffe [8–10], wie auch die Anzahl der verfügbaren Normen veranschaulicht. Bei Kunststoffen, speziell Verbundwerkstoffen (siehe auch: Prüfung von Verbundwerkstoffen) oder Laminaten, steht eine größere Anzahl von Prüfnormen zur Verfügung, da die Scherung bei diesen Werkstoffen der Automobil- und Luftfahrtindustrie infolge des Lagenaufbaus und der genutzten Klebetechniken eine relevante Belastungsart darstellt.
| Bild 4: | Schematische Darstellung des Scherversuches bei Zug- und Druckbeanspruchung (a) zweischnittig und (b) einschnittig |
Die Scherversuche zur Ermittlung des Schermoduls G können an runden oder prismatischen Prüfköpern durchgeführt werden. Dabei ist auf scharfe Scherkanten des Prüfwerkzeugs und exakte Positionierung der Auflager zu achten, um den Biegeanteil im Prüfergebnis zu minimieren. Die Schubspannung τ kann vereinfacht durch Normierung der gemessenen Kraft F auf die jeweilige Querschnittsfläche A = b · h oder A = π d2/4 ermittelt werden. Eine exaktere Lösung ergibt sich bei Verwendung des gemessenen Traversenwegs. In diesem Fall ist für die Fläche des prismatischen Prüfkörpers A = b · Δl anzusetzen, wogegen bei dem runden Prüfkörper die Kreissektorfläche As zu verwenden ist, die in einschlägigen Tabellenbüchern zu finden ist.
Der Scherwinkel γ kann aus dem ermittelten Traversenweg für die einschnittige Scherung nach Gl. (7) und die zweischnittige Belastung nach Gl. (8) berechnet werden.
| (7) |
| (8) |
Der Schermodul G ergibt sich dann nach der Gl. (5) oder (6), je nachdem, ob der Tangenten- oder Sekantenmodul verwendet wird. Erfahrungsgemäß tritt bei diesen Scherversuchen ein mehr oder minder ausgeprägtes Anlaufverhalten auf, so dass ein Offset bei der Ermittlung des Moduls berücksichtigt werden muss.
Dynamisch-Mechanische Analyse (DMA) bei Torsionsbeanspruchung
Die dynamisch-mechanische Analyse (DMA) oder dynamisch mechanisch thermische Analyse (DMTA) unter Nutzung der Torsionsbeanspruchung kann grundsätzlich mit zwei Prüfverfahren,
durchgeführt werden.
Bei der dynamisch-mechanischen Analyse wird ein Prüfkörper mit einer vorgegebenen Geometrie einer periodisch wechselnden Beanspruchung ausgesetzt. Durch die Variation der Frequenz ist die Charakterisierung der Zeitabhängigkeit des Werkstoffverhaltens bei konstanter Temperatur möglich. Wenn diese Untersuchungen in einer Temperierkammer durchgeführt werden, wird die Prüfmethode als DMTA bezeichnet und es wird die Temperaturabhängigkeit des dynamischen Schubmoduls für die zu untersuchenden Werkstoffe charakterisiert [11−13].
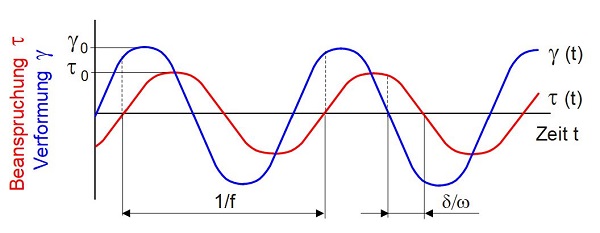
Für die Charakterisierung der viskoelastischen Eigenschaften von Kunststoffen unter Verwendung erzwungener Schwingungen wird der Prüfkörper einer sinusförmig wechselnden mechanischen Beanspruchung mit konstanter Frequenz und konstanter Amplitude ausgesetzt (Bild 5). Bei linear-viskoelastischem Verhalten weisen die zeitlichen Änderungen von Spannung τ und Deformation γ im eingeschwungenen Zustand die gleiche Frequenz aber unterschiedliche Phasenlagen auf. Der Wert δ ist der Phasenwinkel, der im Bereich zwischen 0 und π/2 liegt. Für den Fall einer Schubspannungsbeanspruchung gelten die Gln. (9) und (10).
| (9) |
| (10) |
| Bild 5: | Zeitliche Änderung von Spannung und Dehnung bei dynamisch-mechanischer Analyse unter Verwendung erzwungener Schwingungen |
Infolge der Phasenverschiebung δ zwischen Beanspruchung (Spannung) und der Verformung (Scherung) ist zur Beschreibung des Spannungs-Scherungs-Zusammenhanges der Modul als komplexe Größe G* nach der Gl. (11) einzuführen.
| (11) |
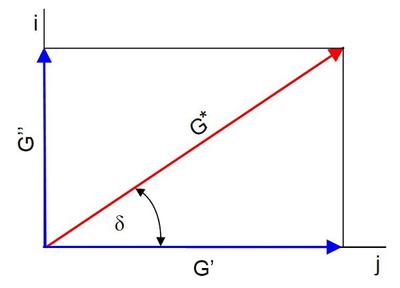
Der komplexe Modul kann als Vektor in der komplexen Zahlenebene betrachtet werden (Bild 6), dessen Richtung durch den Phasenwinkel δ und dessen Betrag durch das Verhältnis der Amplitudenwerte von Spannung und Dehnung gegeben ist.
| Bild 6: | Darstellung des Moduls G* in der komplexen Zahlenebene |
Der Absolutbetrag des jeweiligen Moduls ergibt sich aus dem Verhältnis der Initialbeanspruchung zur Ausgangsverformung nach der Gl. (12).
| (12) |
Unter Verwendung einfacher trigonometrischer Beziehungen ist eine Aufteilung in den Realteil G‘ und den Imaginärteil G‘‘ möglich, die mit den Gln. (13) und (14) vorgenommen wird. Der Realteil G‘ wird als Speichermodul bezeichnet und ist ein Maß für die während einer Schwingungsperiode gespeicherte reversible Energie. Der Imaginäranteil G‘‘ entspricht der in der Periode dissipierten Energie und wird Verlustmodul genannt.
| (13) |
| (14) |
Das Verfahren der erzwungenen Torsionsschwingungen ist auf Frequenzen unterhalb der Resonanzfrequenz des Prüfkörpers beschränkt. Kommerzielle Geräte arbeiten im Bereich von ca. 10-2 Hz bis 102 Hz, wobei als Messgröße die Leistungsaufnahme des Antriebmotors dient. Wird z. B. infolge der Erhöhung der Prüftemperatur der Glasübergang (siehe: Glastemperatur) erreicht, dann steigt die Dämpfung stark an und die Leistung des Motors muss zur Aufrechterhaltung der Prüffrequenz und Spannungs- oder Verformungsamplitude erhöht werden.
Die Messung kann sowohl dehnungs- als auch spannungsgeregelt erfolgen, was die Bestimmung des komplexen Moduls G* und der komplexen Nachgiebigkeit C* = 1 / G* ermöglicht. Dies gestattet die Ermittlung komplexer Schermoduli in einem weiten Steifigkeitsbereich von ca. 10-3 MPa bis 106 MPa. Der größte Nachteil des Verfahrens liegt in der geringen Empfindlichkeit bei der Messung von Kunststoffen mit sehr kleiner Dämpfung (tan δ < 0,01), d. h. sehr steifen oder hochmoduligen Werkstoffen (siehe: Elastizitätsmodul Beispiele Kennwertermittlung).
Gerätesysteme für DMA- und DMTA-Untersuchungen
Auf Grund ihrer hohen Anwendungsbreite besitzen Prüfverfahren mit erzwungenen Schwingungen heute eine hohe Bedeutung bei der dynamisch-mechanischen Analyse polymerer Werkstoffe.
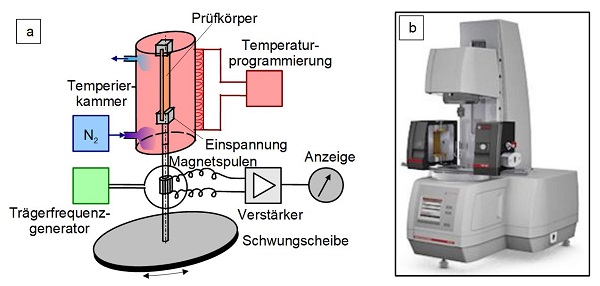
| Bild 7: | (a) Schematische Darstellung eines DMTA-System und (b) DMA-System der Fa. Anton Paar GmbH, Graz, Österreich |
In den meisten Anwendungen nutzt man jedoch Tischprüfsysteme (Stand Alone Systeme) für kleinere Prüfkräfte (Bild 7). Gemeinsam ist allen Verfahren, dass die Deformation des Prüfkörpers sehr klein ist und den linear-viskoelastischen Bereich nicht überschreiten sollte. Infolge dieser kleinen Verformungen sind mit der DMA oder DMTA im Temperaturintervall von ca. –180 °C bis 400 °C hohe Prüffrequenzen bei mechanischer Anregung bis zu 100 Hz realisierbar. Bei den Tischprüfsystemen existiert in Abhängigkeit von der Ausstattung eine große Auswahl an kommerziellen Prüfsystemen, wobei diese in der Regel mit Zusatzeinrichtungen ausgestattet sind.
Ermittlung von Modul-Temperatur-Kurven
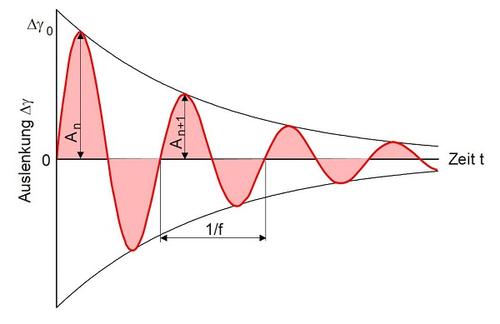
Die freien gedämpften Schwingungen werden eigentlich nur bei Messungen mit dem Torsionspendel angewandt, wobei hier wesentlich niedrige Messfrequenzen möglich sind. Wird ein Prüfkörper durch eine einmalige impulsartige Verformung aus seiner Ruhelage ausgelenkt, so kehrt er in freien gedämpften Schwingungen in den Gleichgewichtszustand zurück. Die Auslenkung sollte dabei den Bereich der linear-viskoelastischen Deformation nicht überschreiten. Die Eigenfrequenz der Schwingung und die zeitliche Abnahme der Schwingungsamplituden (Dämpfung) sind dabei von den viskoelastischen Eigenschaften des untersuchten Werkstoffs und der Prüftemperatur abhängig (Bild 8).
Die freien gedämpften Schwingungen werden bei Frequenzen im Bereich von 0,1 bis 10 Hz genutzt, wobei hier die Untersuchung von Werkstoffen mit geringer Dämpfung von tan δ ≤ 0,1 bevorzugt wird. Da bei Untersuchungen in Abhängigkeit von der Temperatur durch die Moduländerung eine Veränderung der Eigenfrequenz des Systems stattfindet, werden Modul-Temperatur-Kurven deshalb in der Regel bei gleitender Frequenz gemessen, wobei eine Kompensation der Frequenzänderungen über Variation des Trägheitsmoments der Schwungmasse prinzipiell möglich ist.
| Bild 8: | Frei abklingende gedämpfte Schwingung |
Das Prinzip der freien gedämpften Schwingungen findet in Form des Torsionspendel Verfahrens technische Anwendung und ist in DIN EN ISO 6721-2 [12] genormt.
Schematischer Aufbau eines Torsionspendels
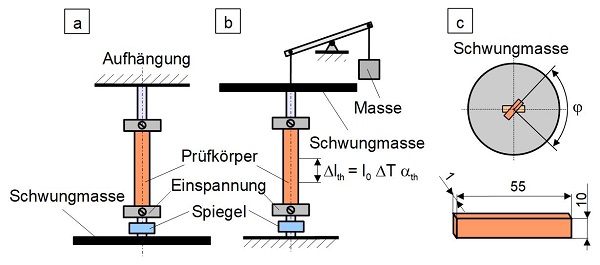
Der prinzipielle Aufbau eines Torsionspendels ist in Bild 9 schematisch dargestellt. Ein vorzugsweise prismatischer Prüfkörper wird an einem Ende fest eingespannt, während das anderen Ende mit einer Schwungmasse verbunden ist, die das Trägheitsmoment und damit die Eigenfrequenz des Gesamtsystems beeinflusst. Gleichzeitig ruft diese Masse allerdings auch eine Ausdehnung infolge der mechanischen und thermischen Belastung hervor (Bild 9a). Zur Vermeidung dieser überlagerten Normalspannungen in Längsrichtung des Prüfkörpers kann ein Gewichtsausgleich durch eine Kompensationsmasse (Bild 9b) verwendet werden. Durch eine impulsartige Initialauslenkung φ der Schwungmasse wird der Prüfkörper zu frei abklingenden Torsionsschwingungen angeregt, wie schematisch in Bild 9c gezeigt.
| Bild 9: | Schematische Darstellung des Aufbaus des Torsionspendels (a) ohne Gewichtsausgleich, (b) mit Gewichtsausgleich und (c) Prüfanordnung mit der Initialauslenkung φ und Prüfkörper |
Aus der Eigenfrequenz der Schwingung kann der Speichermoduls G‘ nach Gl. (15) ermittelt werden [3].
| (15) |
Dabei ist fd die Eigenfrequenz des Pendels mit Prüfkörper und f0 die Eigenfrequenz des Pendels ohne Prüfkörper (bei Arbeit ohne Gewichtsausgleich ist f0 = 0). Als weitere Einflussgrößen sind das Trägheitsmoment Ip der Schwungmasse mit Einspannung sowie ein Dämpfungskorrekturfaktor Fd und der Geometriefaktor Fg zu berücksichtigen. Bei Verwendung von prismatischen Prüfkörpern mit der Einspannlänge L, der Breite b, der Dicke h und einem h/b-Verhältnis ≤ 6 ergibt sich der geometrische Korrekturfaktor zu Fc = 1 − 0,63 h/b, wodurch sich G‘ dann nach Gl. (16) berechnet.
| (16) |
Eine näherungsweise Ermittlung des Schubmoduls G‘ ist auch bei Verwendung des Zugschwingversuchs aus dem E-Modul E‘ oder mit dem E-Modul im Zugversuch Et möglich, falls die Poissonzahl µ im entsprechenden Temperaturintervall bekannt ist (Gl. 17).
| (17) |
Ultraschallprüfung (Wellenausbreitung)
Im Bereich hoher Frequenzen kann der dynamische Schubmodul G‘ auch durch die Verwendung von Ultraschallwellen (siehe Ultraschallprüfung) zur Ermittlung von Kennwerten herangezogen werden [14], falls Transversalwellen und Winkelprüfköpfe eingesetzt werden.
Oberhalb der Resonanzfrequenz wird die Wellenlänge λ der schwingenden mechanischen Beanspruchung klein im Vergleich zu den Prüfkörperabmessungen. Damit ist es möglich, die Charakteristik der Wellenausbreitung im Werkstoff zur Bestimmung der viskoelastischen Eigenschaften zu nutzen. Die Messungen werden üblicherweise mittels Ultraschall (f > 20 kHz) im Impuls-Echo- oder Durchschallungsverfahren durchgeführt [14]. Dabei werden die Schallgeschwindigkeiten c (Gl. 18) und der Schallabsorptionskoeffizient α (Gl.19) aus der akustischen Weglänge d und der zugehörigen Impulslaufzeit t sowie den Amplituden A1 und A2 bei unterschiedlichen Weglängen d1 und d2 ermittelt, wobei hier der Einschallwinkel β des Prüfkopfs zu beachten ist.
| (18) |
| (19) |
Unter Verwendung von Transversalwellen (cT, αT) kann bei Kenntnis der Dichte ρ des Werkstoffs der Schubmodul G bestimmt werden. Bei geringer Dämpfung (αλ/2π << 1) gilt dann näherungsweise die Gl. (20).
| und | (20) |
Ultraschallmessungen finden üblicherweise bei Frequenzen zwischen 100 kHz und 100 MHz statt. Das obere Ende des Frequenzbereiches ist dabei durch die starke Zunahme der Dämpfung gegeben. Für die Arbeit in diesem weiten Frequenzbereich ist die Verwendung unterschiedlicher Schwingungssensoren erforderlich. Relativ große Frequenzbereiche können nach einer breitbandigen Anregung mit Hilfe der Fourier- oder Wavelet-Analyse erfasst werden.
Eine relativ einfache Methode zur Bestimmung des Schubmoduls mit Ultraschall ist bei Verwendung von plattenförmigen Prüfkörpern bekannter Dicke d und Dichte ρ gegeben (Bild 10).
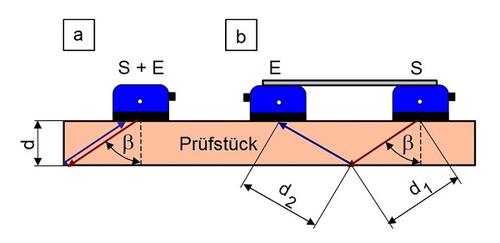
| Bild 10: | Schematische Darstellung der (a) Impuls-Echo-Technik und (b) Durchschallungstechnik mit Winkelprüfköpfen |
Bei Verwendung von Winkelprüfköpfen (Bild 6a und b) werden Transversalwellen zur Messung genutzt, wobei zu beachten ist, dass bei der Impuls-Echo-Technik die Laufzeit des Ultraschalls in etwa identisch wie bei der Durchschallungsmethode ist. Aus dem A-Bild kann dann die Laufzeit Δt in Direktankopplung oder Tauchbadtechnik bei bekannter Dicke d und Einschallwinkel β nach Gl. (21) die Transversalwellengeschwindigkeit cT berechnet werden.
| (21) |
Unter Voraussetzung, dass die Prüftemperatur T bekannt ist, kann dann nach Gl. (22) der Schubmodul G berechnet werden, wobei zu beachten ist, dass dieser Kennwert frequenzabhängig ist.
| (22) |
Literaturhinweise
| [1] | Lüpke, T.: Grundlagen mechanischen Verhaltens. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage S. 91/92, (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18) |
| [2] | ASTM A 938 (2018): Standard Test Method for Torsion Testing of Wire |
| [3] | DIN ISO 7800 (2013-09): Metallische Werkstoffe – Draht − Einfacher Verwindeversuch |
| [4] | DIN 51212 (1978-09): Prüfung metallischer Werkstoffe − Verwindeversuch an Drähten (zurückgezogen) |
| [5] | DIN EN 408 (2012-10): Holzbauwerke – Bauholz für tragende Zwecke und Brettschichtholz − Bestimmung einiger physikalischer und mechanischer Eigenschaften |
| [6] | Göldner, H. (Hrsg.): Arbeitsbuch Höhere Festigkeitslehre. Fachbuch Verlag Leipzig, (1978) S. 163–167 (siehe AMK-Büchersammlung unter T 13) |
| [7] | Wawrziniok, O.: Handbuch des Materialprüfwesens. Springer Verlag, Berlin (1923), (ISBN 978-3-642-90524-7) |
| [8] | DIN 50141 (1982-01): Prüfung metallischer Werkstoffe – Scherversuch (zurückgezogen) |
| [9] | DIN EN 28749 (1992-10): Stifte und Kerbstifte – Scherversuch |
| [10] | DIN EN 789 (2005-01): Holzbauwerke – Prüfverfahren – Bestimmung der mechanischen Eigenschaften von Holzwerkstoffen |
| [11] | DIN EN ISO 6721-1 (2019-09): Kunststoffe – Bestimmung dynamisch-mechanischer Eigenschaften – Teil 1: Allgemeine Grundlagen |
| [12] | DIN EN ISO 6721-2 (2019-09): Kunststoffe − Bestimmung dynamisch-mechanischer Eigenschaften − Teil 2: Torsionspendel-Verfahren |
| [13] | ISO 6721-8 (2019-04): Kunststoffe – Bestimmung dynamisch-mechanischer Eigenschaften – Teil 8: Längs- und Scherschwingung – Wellenausbreitungs-Verfahren |
| [14] | Matthies, K. u. a.: Dickenmessung mit Ultraschall. DVS-Verlag GmbH, Berlin, 2. Auflage (1998), (ISBN 3-87155-940-7; siehe AMK-Büchersammlung unter M 44) |