Zeit-Temperatur-Verschiebungsgesetz
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Zeit-Temperatur-Verschiebungsgesetz
Allgemeines
Das Zeit-Temperatur-Verschiebungsgesetz wird in der Literatur [1] auch als Zeit-Temperatur-Superpositionsprinzip bezeichnet. Viskoelastische Materialien weisen neben der ausgeprägten Zeitabhängigkeit auch eine starke Temperaturabhängigkeit der Eigenschaften auf. Die Ursache dafür liegt in den molekularen Bewegungs- und Umlagerungsvorgängen begründet, die das Relaxations- bzw. Retardationsspektrum des Materials bestimmen.
Die Zeit-Temperatur-Äquivalenz
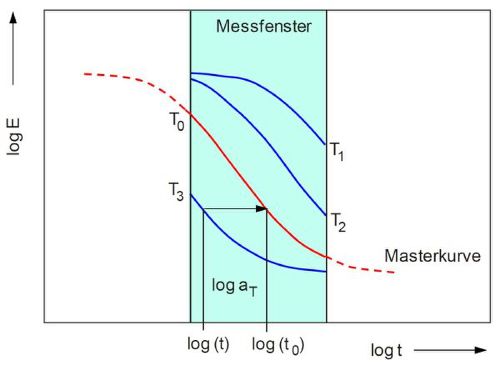
Als thermisch aktivierbare Prozesse laufen diese molekularen Vorgänge bei Zunahme der Temperatur mit wachsender Geschwindigkeit ab. Dadurch verschieben sich Relaxations- und Retardationszeitspektrum zu kürzeren Zeiten. Ändert sich in Abhängigkeit von der Temperatur nur die Geschwindigkeit der molekularen Prozesse, nicht jedoch ihre Art und Anzahl, so bleibt die Form des Relaxations- bzw. Retardationsspektrums und damit auch die Gestalt der viskoelastischen Kennwertfunktionen entlang der logarithmischen Zeitachse erhalten. Ihre zeitliche Lage ändert sich jedoch entsprechend der Temperatur. Eine Konsequenz dieses als "thermorheologisch einfach" bezeichneten Verhaltens ist die Zeit-Temperatur-Äquivalenz, deren Anwendung in Form des Zeit-Temperatur-Superpositionsprinzips große praktische Bedeutung für die Vorhersage des Langzeitverhaltens (siehe: Zeitstandzugversuch) erlangt hat. Ist der Verlauf einer viskoelastischen Kenngröße, zum Beispiel des Moduls E(log t), in einem bestimmten Zeitintervall bei unterschiedlichen Temperaturen bekannt, so können die einzelnen Kurvenverläufe, wie in Bild 1 schematisch dargestellt, durch horizontale Verschiebung mit der bei der Referenztemperatur T0 ermittelten Kurve E0(log t) zur Deckung gebracht werden.
| Bild 1: | Schema der Masterkurvenkonstruktion durch Zeit-Temperatur-Superposition |
Damit entsteht eine Masterkurve, die das Werkstoffverhalten über einen weiten Zeitbereich abbildet. Die Verschiebungsfunktion log aT = log t – log t0 ist temperaturabhängig. Sie kann in vielen Fällen auf Grundlage eines ARRHENIUS-Ansatzes beschrieben werden:
| (1) |
Im Bereich des Glasübergangs (siehe auch Glastemperatur) folgt sie jedoch häufig der WILLIAMS, LANDEL und FERRY (WLF)-Gleichung:
| (2) |
mit den universellen Konstanten C1 und C2 [2].
Literaturhinweise
| [1] | Lüpke, T.: Grundlagen mechanischen Verhaltens. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 92/93, (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18) |
| [2] | Williams, M. L., Landel, R. F., Ferry, J. D.: The Temperature Dependence of Relaxation Mechanism in Amorphous Polymers and other Glass-forming Liquids. J. Amer. Chem. Soc. 77 (1955) 3701−3707 |