Griffith-Kriterium: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
| − | < | + | <span style="font-size:1.2em;font-weight:bold;">Griffith – Kriterium</span> |
'''Rissbruchkriterium nach Griffith''' | '''Rissbruchkriterium nach Griffith''' | ||
Die Energiebilanz für den Fall einer [[Rissausbreitung]] in einer unendlich ausgedehnten Platte mit endlicher Dicke wurde erstmals von Griffith [1] diskutiert. Nach Griffith tritt Rissfortschritt dann ein, wenn die durch Verlängerung des Anrisses freiwerdende '''elastische Verzerrungsenergie W<sub>e</sub>''' gleich oder größer ist als die zur Bildung der Bruchflächen benötigte '''Oberflächenenergie W<sub>o</sub>''', d.h. | Die Energiebilanz für den Fall einer [[Rissausbreitung]] in einer unendlich ausgedehnten Platte mit endlicher Dicke wurde erstmals von Griffith [1] diskutiert. Nach Griffith tritt Rissfortschritt dann ein, wenn die durch Verlängerung des Anrisses freiwerdende '''elastische Verzerrungsenergie W<sub>e</sub>''' gleich oder größer ist als die zur Bildung der Bruchflächen benötigte '''Oberflächenenergie W<sub>o</sub>''', d.h. | ||
| − | + | {| | |
| − | <math>W_e\, \ge \, W_o</math> | + | |- |
| + | |width="20px"| | ||
| + | |width="500px" | <math>W_e\, \ge \, W_o</math> | ||
| + | |} | ||
Das Kriterium der instabilen Rissausbreitung lautet | Das Kriterium der instabilen Rissausbreitung lautet | ||
| − | + | {| | |
| − | <math>\frac{dW_e}{da}\, \ge \, \frac{dW_o}{da}</math> | + | |- |
| + | |width="20px"| | ||
| + | |width="500px" | <math>\frac{dW_e}{da}\, \ge \, \frac{dW_o}{da}</math> | ||
| + | |} | ||
Als '''elastische Verzerrungsenergie W<sub>e</sub>''' wird | Als '''elastische Verzerrungsenergie W<sub>e</sub>''' wird | ||
| + | {| | ||
| + | |- | ||
| + | |width="20px"| | ||
| + | |width="500px" | <math>W_e\,=\,\frac{\pi \sigma^2 a^2}{E}</math> | ||
| + | |} | ||
| − | + | mit | |
{| | {| | ||
| + | |- | ||
|a | |a | ||
| − | | | + | |width="15px" | |
|Risslänge | |Risslänge | ||
|- | |- | ||
|E | |E | ||
| − | | | + | | |
|Elastizitätsmodul | |Elastizitätsmodul | ||
| + | |} | ||
| + | |||
| + | angenommen, während die '''Oberflächenenergie W<sub>o</sub>''' für beide Bruchflächen | ||
| + | {| | ||
|- | |- | ||
| + | |width="20px"| | ||
| + | |width="500px" | <math>W_o\,=\,4\, a\, \gamma_o</math> | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| + | mit | ||
{| | {| | ||
| + | |- | ||
|<math>\gamma</math><sub>o</sub> | |<math>\gamma</math><sub>o</sub> | ||
| − | | | + | |width="15px" | |
|Oberflächenspannung | |Oberflächenspannung | ||
| − | |||
|} | |} | ||
| Zeile 38: | Zeile 54: | ||
Das Kriterium der [[Rissausbreitung]] führt dann zu | Das Kriterium der [[Rissausbreitung]] führt dann zu | ||
| − | + | {| | |
| − | <math>\frac{2\, a\, \pi\, \sigma^2}{E} \, \ge \, 4\, \gamma_o</math> | + | |- |
| + | |width="20px"| | ||
| + | |width="500px" | <math>\frac{2\, a\, \pi\, \sigma^2}{E} \, \ge \, 4\, \gamma_o</math> | ||
| + | |} | ||
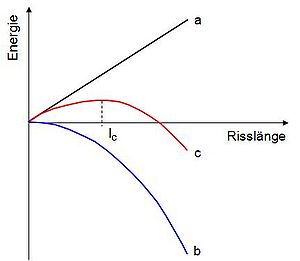
Unter diesen Bedingungen breitet sich ein vorhandener Riss instabil, d.h. ohne äußere Energiezufuhr aus (Bild). | Unter diesen Bedingungen breitet sich ein vorhandener Riss instabil, d.h. ohne äußere Energiezufuhr aus (Bild). | ||
[[Datei:Griffith-Kriterium.jpg|300px]] | [[Datei:Griffith-Kriterium.jpg|300px]] | ||
| + | {| | ||
| + | |- valign="top" | ||
| + | |width="50px"|'''Bild''': | ||
| + | |width="600px" |Energiebilanz bei der instabilen Rissausbreitung [2]<br>a) Oberflächenenergie<br>b) elastische Verzerrungsenergie<br>c) Gesamtenergie | ||
| + | |} | ||
| + | |||
| + | Für die zur Rissausbreitung erforderliche Spannung erhält man | ||
{| | {| | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| + | |width="20px"| | ||
| + | |width="500px" | <math>\sigma_c\,=\,\sqrt{\frac{2 E \gamma_o}{\pi a}}</math> | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
während die zugehörige kritische Risslänge (Griffith-Länge) a<sub>o</sub> | während die zugehörige kritische Risslänge (Griffith-Länge) a<sub>o</sub> | ||
| − | + | {| | |
| − | <math>a_o\,=\,\frac{2 E \gamma_o}{\pi \sigma^2}</math> | + | |- |
| + | |width="20px"| | ||
| + | |width="500px" | <math>a_o\,=\,\frac{2 E \gamma_o}{\pi \sigma^2}</math> | ||
| + | |} | ||
beträgt. | beträgt. | ||
| Zeile 76: | Zeile 92: | ||
'''Hypothese 2:''' Das Risswachstum erfolgt, falls J<sub>e</sub> ≥ 2<math>\gamma</math><sub>o</sub> mit J<sub>e</sub> – elastsicher Anteil. Die Rissausbreitung verläuft instabil, wenn gilt: | '''Hypothese 2:''' Das Risswachstum erfolgt, falls J<sub>e</sub> ≥ 2<math>\gamma</math><sub>o</sub> mit J<sub>e</sub> – elastsicher Anteil. Die Rissausbreitung verläuft instabil, wenn gilt: | ||
| + | {| | ||
| + | |- | ||
| + | |width="20px"| | ||
| + | |width="500px" | <math>\frac{\delta K_I}{\delta a}\, \ge \, 0</math> | ||
| + | |} | ||
| − | |||
| − | '''Literaturhinweise | + | '''Literaturhinweise''' |
{| | {| | ||
|- valign ="top" | |- valign ="top" | ||
|[1] | |[1] | ||
| − | | Griffith, A.A.: The phenomena of rupture and flow in solids. Phil. Trans. Roy. Soc. London, Series A, Vol. 221 (1920) 163–198 | + | |[[Griffith, A.A.]]: The phenomena of rupture and flow in solids. Phil. Trans. Roy. Soc. London, Series A, Vol. 221 (1920) 163–198 |
|- valign ="top" | |- valign ="top" | ||
|[2] | |[2] | ||
| − | |Blumenauer, H., Pusch, G.: Bruchmechanik – Grundlagen, Prüfmethoden, Anwendungsgebiete. Deutscher Verlag für Grundstoffindustrie, Leipzig (1973) S. 37–38 (siehe [http://www.hs-merseburg.de/amk/index.php?option=com_joomlib&Itemid=85 AMK-Büchersammlung] unter E 28) | + | |[[Blumenauer, Horst|Blumenauer, H.]], Pusch, G.: Bruchmechanik – Grundlagen, Prüfmethoden, Anwendungsgebiete. Deutscher Verlag für Grundstoffindustrie, Leipzig (1973) S. 37–38 (siehe [http://www.hs-merseburg.de/amk/index.php?option=com_joomlib&Itemid=85 AMK-Büchersammlung] unter E 28) |
|- valign ="top" | |- valign ="top" | ||
|[3] | |[3] | ||
| − | |Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig (1987) 2. Auflage S. 22 (ISBN 3-342-00096-1) (siehe [http://www.hs-merseburg.de/amk/index.php?option=com_joomlib&Itemid=85 AMK-Büchersammlung] unter E 29-2) | + | |[[Blumenauer, Horst|Blumenauer, H.]], Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig (1987) 2. Auflage S. 22 (ISBN 3-342-00096-1) (siehe [http://www.hs-merseburg.de/amk/index.php?option=com_joomlib&Itemid=85 AMK-Büchersammlung] unter E 29-2) |
|- valign ="top" | |- valign ="top" | ||
|[4] | |[4] | ||
|Sähn, S., Göldner, H.: Bruch- und Beurteilungskriterien in der Festigkeitslehre. Fachbuchverlag, Leipzig Köln (1993) 2. Auflage, S. 139 (ISBN 3-343-00854-0) (siehe [http://www.hs-merseburg.de/amk/index.php?option=com_joomlib&Itemid=85 AMK-Büchersammlung] unter E 26) | |Sähn, S., Göldner, H.: Bruch- und Beurteilungskriterien in der Festigkeitslehre. Fachbuchverlag, Leipzig Köln (1993) 2. Auflage, S. 139 (ISBN 3-343-00854-0) (siehe [http://www.hs-merseburg.de/amk/index.php?option=com_joomlib&Itemid=85 AMK-Büchersammlung] unter E 26) | ||
| − | |||
|} | |} | ||
Version vom 18. Dezember 2012, 13:53 Uhr
Griffith – Kriterium
Rissbruchkriterium nach Griffith
Die Energiebilanz für den Fall einer Rissausbreitung in einer unendlich ausgedehnten Platte mit endlicher Dicke wurde erstmals von Griffith [1] diskutiert. Nach Griffith tritt Rissfortschritt dann ein, wenn die durch Verlängerung des Anrisses freiwerdende elastische Verzerrungsenergie We gleich oder größer ist als die zur Bildung der Bruchflächen benötigte Oberflächenenergie Wo, d.h.
Das Kriterium der instabilen Rissausbreitung lautet
Als elastische Verzerrungsenergie We wird
mit
| a | Risslänge | |
| E | Elastizitätsmodul |
angenommen, während die Oberflächenenergie Wo für beide Bruchflächen
mit
| o | Oberflächenspannung |
beträgt.
Das Kriterium der Rissausbreitung führt dann zu
Unter diesen Bedingungen breitet sich ein vorhandener Riss instabil, d.h. ohne äußere Energiezufuhr aus (Bild).
| Bild: | Energiebilanz bei der instabilen Rissausbreitung [2] a) Oberflächenenergie b) elastische Verzerrungsenergie c) Gesamtenergie |
Für die zur Rissausbreitung erforderliche Spannung erhält man
während die zugehörige kritische Risslänge (Griffith-Länge) ao
beträgt.
Experimentelle Untersuchungen haben die Brauchbarkeit der Beziehung für die kritische Spannung und Risslänge bei extrem spröden Werkstoffverhalten bestätigt [3].
Die beiden Grundhypothesen des Griffith-Kriterium lauten [4]:
Hypothese 1: Der Riss breitet sich in Rissrichtung aus.
Hypothese 2: Das Risswachstum erfolgt, falls Je ≥ 2o mit Je – elastsicher Anteil. Die Rissausbreitung verläuft instabil, wenn gilt:
Literaturhinweise
| [1] | Griffith, A.A.: The phenomena of rupture and flow in solids. Phil. Trans. Roy. Soc. London, Series A, Vol. 221 (1920) 163–198 |
| [2] | Blumenauer, H., Pusch, G.: Bruchmechanik – Grundlagen, Prüfmethoden, Anwendungsgebiete. Deutscher Verlag für Grundstoffindustrie, Leipzig (1973) S. 37–38 (siehe AMK-Büchersammlung unter E 28) |
| [3] | Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig (1987) 2. Auflage S. 22 (ISBN 3-342-00096-1) (siehe AMK-Büchersammlung unter E 29-2) |
| [4] | Sähn, S., Göldner, H.: Bruch- und Beurteilungskriterien in der Festigkeitslehre. Fachbuchverlag, Leipzig Köln (1993) 2. Auflage, S. 139 (ISBN 3-343-00854-0) (siehe AMK-Büchersammlung unter E 26) |