Risswiderstandskurve – Elastomere quasistatisch: Unterschied zwischen den Versionen
| Zeile 100: | Zeile 100: | ||
|-valign="top" | |-valign="top" | ||
|[1] | |[1] | ||
| − | |Reincke, K.: Elastomere Werkstoffe – Zusammenhang zwischen Mischungsrezeptur, Struktur und mechanischen Eigenschaften sowie dem Deformations- und Bruchverhalten, Habilitation, Martin-Luther-Universität Halle-Wittenberg, Shaker Verlag (2016) (ISBN 978-3-8440-4637-3; siehe [[AMK-Büchersammlung]] unter B 2-2) | + | |[[Reincke,_Katrin|Reincke, K.]]: Elastomere Werkstoffe – Zusammenhang zwischen Mischungsrezeptur, Struktur und mechanischen Eigenschaften sowie dem Deformations- und Bruchverhalten, Habilitation, Martin-Luther-Universität Halle-Wittenberg, Shaker Verlag (2016) (ISBN 978-3-8440-4637-3; siehe [[AMK-Büchersammlung]] unter B 2-2) |
|-valign="top" | |-valign="top" | ||
|[2] | |[2] | ||
| − | |[[Grellmann,_Wolfgang|Grellmann, W.]], Reincke, K.: Technical Material Diagnostics – Fracture Mechanics of Filled Elastomer Blends. In: Grellmann, W., Heinrich, G., Kaliske, M., Klüppel, M., Schneider, K., Vilgis, T. (Eds.): Fracture Mechanics and Statistical Mechanics of Reinforced Elastomeric Blends. Springer Verlag Berlin Heidelberg, (2013), S. 227–268, (ISBN 978-3-642-37909-3; siehe [[AMK-Büchersammlung]] unter A 14) | + | |[[Grellmann,_Wolfgang|Grellmann, W.]], Reincke, K.: Technical Material Diagnostics – Fracture Mechanics of Filled Elastomer Blends. In: [https://www.researchgate.net/profile/Wolfgang-Grellmann Grellmann, W.], [https://de.wikipedia.org/wiki/Gert_Heinrich Heinrich, G.], Kaliske, M., Klüppel, M., Schneider, K., [https://de.wikipedia.org/wiki/Thomas_A._Vilgis Vilgis, T.] (Eds.): Fracture Mechanics and Statistical Mechanics of Reinforced Elastomeric Blends. Springer Verlag Berlin Heidelberg, (2013), S. 227–268, (ISBN 978-3-642-37909-3; siehe [[AMK-Büchersammlung]] unter A 14) |
|-valign="top" | |-valign="top" | ||
|[3] | |[3] | ||
| − | |Reincke, K., Oßwald, K., Grellmann, W.: Experimental Investigations fpr Characterization of Crack Toughness of Filler-reinforced SBR Vulcanizates. 11. Tagung "Problemseminar: Deformation und Bruchverhalten von Kunststoffen", 20.–22.06.2007, Merseburg, Tagungsband CD-ROM (ISBN 978-3-86010-918-2), S. 131–141 | + | |Reincke, K., Oßwald, K., [https://de.wikipedia.org/wiki/Wolfgang_Grellmann Grellmann, W.]: Experimental Investigations fpr Characterization of Crack Toughness of Filler-reinforced SBR Vulcanizates. 11. Tagung "Problemseminar: Deformation und Bruchverhalten von Kunststoffen", 20.–22.06.2007, Merseburg, Tagungsband CD-ROM (ISBN 978-3-86010-918-2), S. 131–141 |
|-valign="top" | |-valign="top" | ||
|[4] | |[4] | ||
| Zeile 127: | Zeile 127: | ||
|-valign="top" | |-valign="top" | ||
|[10] | |[10] | ||
| − | |Netzker, C., Horst, T., Reincke, K., Behnke, R., Kaliske, M., Heinrich, G., Grellmann, W.: Analysis of Stable Crack Propagation in Filled Rubber Based on a Global Energy Balance. Int. J. Fract. 181 (2013) 12–23 | + | |Netzker, C., Horst, T., Reincke, K., Behnke, R., Kaliske, M., Heinrich, G., Grellmann, W.: Analysis of Stable Crack Propagation in Filled Rubber Based on a Global Energy Balance. Int. J. Fract. 181 (2013) 12–23 DOI: [https://doi.org/10.1007/s10704-013-9816-5 https://doi.org/10.1007/s10704-013-9816-5] |
|-valign="top" | |-valign="top" | ||
|[11] | |[11] | ||
| Zeile 136: | Zeile 136: | ||
|-valign="top" | |-valign="top" | ||
|[13] | |[13] | ||
| − | |Stoček, R.: Dynamische Rissausbreitung in Elastomerwerkstoffen. Dissertation, Technische Universität Chemnitz (2012) | + | |Stoček, R.: [https://www.researchgate.net/publication/279845036_Dynamische_Rissausbreitung_in_Elastomerwerkstoffen Dynamische Rissausbreitung in Elastomerwerkstoffen.] Dissertation, Technische Universität Chemnitz (2012) |
|-valign="top" | |-valign="top" | ||
|[14] | |[14] | ||
Aktuelle Version vom 9. Juli 2024, 12:08 Uhr
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Risswiderstandskurve – Elastomere quasistatisch
Aufnahme von R-Kurven mit Hilfe quasistatischer Bruchmechanikversuche
Zur Beschreibung des Risszähigkeitsverhaltens elastomerer Werkstoffe als Widerstand gegen stabile Rissinitiierung und -ausbreitung werden häufig quasistatische Bruchmechanikversuche mit Hilfe einer Universalprüfmaschine durchgeführt. Bei diesem Experiment wird unter Verwendung eines Prüfkörpers (Einprobenmethode) oder mehrerer gleicher Prüfkörper (Mehrprobenmethode) durch gleichzeitige Aufzeichnung des Kraft-Verlängerungs-Diagramms und der Kerböffnung lR die Aufnahme einer Risswiderstandskurve (R-Kurve) ermöglicht.
Die Erfahrungen der letzten Jahre [1‒4] haben gezeigt, dass die Anwendung einer Einprobenmethode (SSM) einen wesentlichen Beitrag zur Aufklärung des stabilen Rissinitiierungs- und Rissausbreitungsverhaltens liefern kann. Der Vorteil dieser Methode im Vergleich zur Mehrprobenmethode (MSM) liegt im reduzierten Materialaufwand und der daraus folgenden Kostenersparnis, die eine Charakterisierung der Zähigkeit unter quasistatischen Versuchsbedingungen bereits im frühen Stadium der Werkstoffentwicklung ermöglicht.
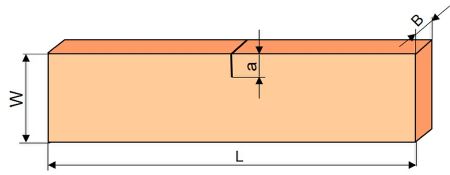
Für die Durchführung von Experimenten können einseitig gekerbte Zugprüfkörper (SENT-Prüfkörper) verwendet werden (siehe Bild 1). Um den ebenen Dehnungszustand während der Beanspruchung sicherzustellen und damit geometrieunabhängige Werkstoffkennwerte zu ermitteln, werden üblicherweise Prüfkörper mit einer Dicke B = 6 mm eingesetzt. Die Länge L der Prüfkörper beträgt 100 mm und die Breite W = 25 mm. Für Standardprüfkörper wird die Kerbtiefe a so gewählt, dass ein a/W-Verhältnis von 0,2 gegeben ist. Die Kerben werden mittels Metallklinge eingebracht (siehe Kerbeinbringung).
| Bild 1: | Schematische Darstellung eines SENT-Prüfkörpers |
Die Beanspruchung der Prüfkörper sollte bei Raumtemperatur je nach Werkstoff mit einer nicht zu hohen Traversengeschwindigkeit von 10 bzw. 50 mm/min erfolgen. Die Einspannlänge beträgt 40 mm.
Ermittlung der physikalischen Initiierung
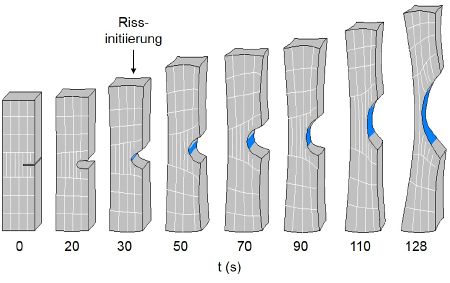
Durch Beobachtung des präparierten Kerbgrundes (siehe: Kerbgeometrie) wird der Zeitpunkt der Rissinitiierung bestimmt, wodurch die Ermittlung physikalischer Rissinitiierungswerte Ji ermöglicht wird. Nach der Rissinitiierung wird der Elastomerprüfkörper im weiteren Versuchsverlauf zunehmend hauptsächlich elastisch deformiert, wobei gleichzeitig die Rissöffnung ebenfalls größer wird. Dieser Vorgang ist schematisch in Bild 2 dargestellt.
| Bild 2: | Schematische Darstellung der größer werdenden Deformation und Rissöffnung (blau) eines SENT-Prüfkörpers aufgrund der äußeren Zugbeanspruchung während eines quasistatischen Bruchmechanikversuches |
Die Präparation des Kerbgrundes erfolgt bei dunklen bzw. schwarzen Werkstoffen mit einem weißen TiO2-Pulver, was stark an der Oberfläche haftet und somit die Entstehung einer neuen Rissoberfläche gut sichtbar werden lässt (siehe Bild 3).
| Bild 3: | Fotosequenz zur Illustration der zunehmenden Rissöffnung während eines quasistatischen Bruchmechanikversuches an einem rußverstärkten Prüfkörper (schwarz) sowie schematische Darstellung zur Definition der Rissöffnung lR, die zunehmend im weiß präparierten Kerbgrund sichtbar wird |
Alternativ können helle Prüfkörper mit dunklem feinteiligem Pulver wie z. B. Ruß präpariert werden, wie es in Bild 4 zu sehen ist. In Anlehnung an Gerber und Struve [5] wurde in [1] jeweils die Strecke zwischen beiden Kerbenden gemessen und der Wert als Schädigungsparameter Rissöffnung lR definiert.
| Bild 4: | Bestimmung der Rissöffnung an einem hellen Prüfkörper, dessen Kerbgrund mit Ruß präpariert wurde |
Zur Ermittlung von J-lR-Wertepaaren wurden mindestens 10 Aufnahmen des Prüfkörpers hinsichtlich der Bestimmung des aktuellen Wertes der Rissöffnung ausgewertet. Weiterhin erfolgte die Bestimmung der Verformungsenergie A zu dem jeweiligen Zeitpunkt aus dem aufgezeichneten Kraft-Traversenweg-Diagramm. Mit Hilfe dieser Daten wurden nach den entsprechenden Zeiten die Verformungsenergiewerte entnommen, die zur Berechnung der J-Werte (siehe: J-Integral-Konzept) dienten.
Mehrprobentechnik
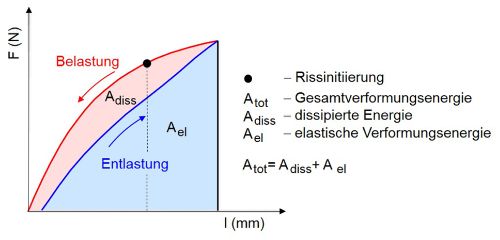
Eine weitere Möglichkeit zur Aufzeichnung von Risswiderstandskurven besteht in der Anwendung des quasistatischen Bruchmechanikversuches und der Mehrprobenmethode, die auch im Rahmen der Untersuchungen in [6‒9] eingesetzt wurde. Hierbei wurden jeweils bis zu 10 gleiche SENT-Prüfkörper mit der identischen Geometrie wie bei den Einprobenversuchen verwendet. Die Beanspruchung wurde ebenfalls mit einer Traversengeschwindigkeit von 10 bis 50 mm/min aufgebracht. Für jeden Prüfkörper wurde der Zeitpunkt der Rissinitiierung wiederum durch Beobachtung des Kerbgrundes definiert. Nach der Rissinitiierung erfolgte die Beanspruchung der Prüfkörper bis zu unterschiedlichen Größen der Rissöffnung. Die Prüfung wurde dann jeweils gestoppt bevor es zum vollständigen Versagen kam. Aus den zugehörigen Kraft-Weg-Diagrammen, die mit der Universalprüfmaschine sowohl während der Be- als auch bei der Entlastung aufgezeichnet wurden, wurden gemäß Bild 5 die beiden Energien Adiss und Atot ermittelt, die zur Berechnung der J-Werte nach Gl. (1) bzw. Gl. (2) als Belastungsparameter der Risswiderstandskurve verwendet wurden.
| (1) |
| (2) |
mit Atot = Adiss + Ael
| Bild 5: | Schematische Darstellung eines Kraft-Traversenweg-Diagrammes aus dem quasistatischen Bruchmechanikversuch/Mehrprobenmethode mit Be- und Entlastungskurve |
Nach der Entlastung im eigentlichen Experiment werden die Prüfkörper erneut geringfügig deformiert und in diesem Zustand mit einer Metallklinge in der Ebene der Rissausbreitung getrennt. In Bild 6 ist beispielhaft eine auf diesem Weg erzeugte Bruchfläche eines 6 mm breiten SENT-Prüfkörpers dargestellt.
| Bild 6: | Aufnahme einer Bruch-/Schnittfläche eines SENT-Prüfkörpers aus dem quasistatischen Bruchmechanikversuch/Mehrprobenmethode zur Illustration des Ausmessens der Größe des stabilen Risswachstums Δa |
Die verschiedenen Bereiche Metallklingenkerb, das stabile Risswachstum Δa und die Schnittfläche im Anschluss an den Bereich des stabilen Risswachstums sind gut erkennbar. Somit kann die Größe von Δa lichtmikroskopisch bestimmt werden. Die Messung von Δa kann z. B. mit einem 3D-Stereomikroskop VHX 500 F der Fa. Keyence erfolgen. In Bild 6 wird dargestellt, wie an jeweils mindestens 8 Stellen über die gesamte Prüfkörperbreite verteilt einzelne Messungen durchgeführt und nachfolgend der Mittelwert bestimmt wird.
Bedeutung der Ein- und Mehrprobentechnik für die Kennwertermittlung
Die Hauptunterschiede zwischen der Ein- und der Mehrprobenmethode bestehen demnach darin, dass die reale Größe des stabilen Risswachstums Δa anstelle der Rissöffnung lR ermittelt wird und dass durch die Aufzeichnung der Belastungs- und Entlastungskurve eine Aufsplittung der totalen Verformungsenergie Atot in die elastische Verformungsenergie Ael und in die dissipierte Energie Adiss möglich ist [7, 10]. Dies ist insofern von Bedeutung, dass abhängig von der Verformbarkeit des untersuchten Werkstoffes auch weit entfernt von der Spitze des Risses eine elastische Verformung auftreten kann. Darüber hinaus wird neben der Energie, die zur Erzeugung der neuen Rissoberfläche ARiss erforderlich ist, im deformierten Volumen elastomerer Werkstoffe auch ein wesentlicher Anteil der äußeren Energie in Form von Energiedissipation umgesetzt. Diese Energiedissipation beinhaltet die Entstehung von Wärme aufgrund innerer Reibung, aber für füllstoffverstärkte Werkstoffe auch den Anteil an Energie der für das Aufbrechen von Füllstoff-Füllstoff- und Füllstoff-Polymer-Bindungen aufgewendet werden muss. Die im Experiment bestimmbare Größe Adiss umfasst also 3 Komponenten: die Energie zur Erzeugung einer neuen Oberfläche, Wärmeenergie und Energie für das Aufbrechen der Bindungen. Nach derzeitigem Erfahrungsstand wird davon ausgegangen, dass der Großteil der Dissipationsprozesse in einem begrenzten Bereich um die Rissspitze herum auftreten, da hier während der Beanspruchung die größten lokalen Spannungen und Dehnungen existieren, wie bereits vielfach auch für Elastomere gezeigt wurde [11‒14].
Die entweder aus der Ein- oder Mehrprobenmethoden gewonnenen J-lR bzw. J-Δa-Werte wurden für die weitere quantitative Auswertung grafisch aufgetragen und mit einer geeigneten Software wurde ein Kurvenfitting mit einer passenden mathematischen Funktion vorgenommen. Als letzte Stufe der Auswertung wurden damit für die Werkstoffe jeweils Rissausbreitungswerte TJ* ermittelt (siehe auch Reißmodul).
Wird während der Anwendung der Mehrprobenmethode zusätzlich die Rissöffnung lR ermittelt, kann überprüft werden, ob es einen funktionalen Zusammenhang zwischen den beiden Schädigungsparametern lR und Δa gibt. Dies ist wegen der teilweise extrem großen elastischen Deformation des gesamten Prüfkörpers insbesondere im Hinblick auf die Aussagefähigkeit der Größe lR und damit auf Anwendbarkeit der Einprobenmethode wichtig.
Literaturhinweise
| [1] | Reincke, K.: Elastomere Werkstoffe – Zusammenhang zwischen Mischungsrezeptur, Struktur und mechanischen Eigenschaften sowie dem Deformations- und Bruchverhalten, Habilitation, Martin-Luther-Universität Halle-Wittenberg, Shaker Verlag (2016) (ISBN 978-3-8440-4637-3; siehe AMK-Büchersammlung unter B 2-2) |
| [2] | Grellmann, W., Reincke, K.: Technical Material Diagnostics – Fracture Mechanics of Filled Elastomer Blends. In: Grellmann, W., Heinrich, G., Kaliske, M., Klüppel, M., Schneider, K., Vilgis, T. (Eds.): Fracture Mechanics and Statistical Mechanics of Reinforced Elastomeric Blends. Springer Verlag Berlin Heidelberg, (2013), S. 227–268, (ISBN 978-3-642-37909-3; siehe AMK-Büchersammlung unter A 14) |
| [3] | Reincke, K., Oßwald, K., Grellmann, W.: Experimental Investigations fpr Characterization of Crack Toughness of Filler-reinforced SBR Vulcanizates. 11. Tagung "Problemseminar: Deformation und Bruchverhalten von Kunststoffen", 20.–22.06.2007, Merseburg, Tagungsband CD-ROM (ISBN 978-3-86010-918-2), S. 131–141 |
| [4] | Reincke, K., Grellmann, W., Heinrich, G.: Engineering Fracture Mechanics for Crack Toughness Characterisation of Elastomers. In: Proceedings of the European Conference of Fracture (ECF 16), Alexandroupolis, Greece, July 3–7 (2006) pp. 507–508 and Full Paper CD: 2T18, (2006) 1–6 |
| [5] | Gerber, G., Struve, J.: Einfluß der Mischungszusammensetzung und Belastungsart auf das Versagensverhalten von Elastomeren. Kautsch. Gummi Kunstst. 52 (1999) 400–405 |
| [6] | Reincke, K.: Bruchmechanische Bewertung von ungefüllten und gefüllten Elastomerwerkstoffen. Mensch & Buch Verlag, Berlin, (2005), (ISBN 978-3-89820-779-9; siehe AMK-Büchersammlung unter B 1-13) |
| [7] | Reincke, K., Grellmann, W., Heinrich, G.: Fracture Mechanical Investigations of Filler-reinforced Elastomers. In: Boukamel, A., Laiarinandrasana, L., Méo, S., Verron, E. (Eds.): Constitutive Models for Rubber V, Taylor & Francis Group London (2008) 221–227 |
| [8] | März, J.: Untersuchungen zur Weiterentwicklung bruchmechanischer Methoden zur quantitativen Beschreibung des Deformations- und Bruchverhaltens von Elastomerwerkstoffen. Diplomarbeit, Martin Luther Universität Halle-Wittenberg (2011), (siehe AMK-Büchersammlung unter B 3-172) |
| [9] | Reincke, K., Grellmann, W.: Mechanical and Fracture Mechanics Properties of Rubber Compositions with Reinforcing Components. In: Galimberti, M. (Ed.): Rubber-Clay Nanocomposites: Science, Technology and Applications. John Wiley & Sons, 1st Edition (2011) 305–342, (ISBN 978-0-470-56210-9; siehe AMK-Büchersammlung unter K 5) |
| [10] | Netzker, C., Horst, T., Reincke, K., Behnke, R., Kaliske, M., Heinrich, G., Grellmann, W.: Analysis of Stable Crack Propagation in Filled Rubber Based on a Global Energy Balance. Int. J. Fract. 181 (2013) 12–23 DOI: https://doi.org/10.1007/s10704-013-9816-5 |
| [11] | Stommel, M.: Beschreibung der viskoelastischen mechanischen Eigenschaften, der Betriebsfestigkeit und des Bruchverhaltens von Elastomerbauteilen mit der Finite‐Elemente‐Methode. IKV – Berichte aus der Kunststoffverarbeitung, Band 92, Verlag Mainz, Wissenschaftsverlag Aachen (1999) |
| [12] | Horst, T.: Spezifische Ansätze zur bruchmechanischen Charakterisierung von Elastomeren, Dissertation, Technische Universität Dresden (2011) TUDpress 2011 (ISBN 978-3-942710-33-6; siehe AMK-Büchersammlung unter K 11) |
| [13] | Stoček, R.: Dynamische Rissausbreitung in Elastomerwerkstoffen. Dissertation, Technische Universität Chemnitz (2012) |
| [14] | Stange, J.: Bruchmechanische Untersuchungen von Elastomeren zur Bewertung des Versagensverhaltens unter besonderer Berücksichtigung der Prüfkörpergeometrie. Diplomarbeit, Martin‐Luther‐Universität Halle‐Wittenberg (2001), (siehe AMK-Büchersammlung unter B 3-97) |