Adhäsive Energiefreisetzungsrate: Unterschied zwischen den Versionen

Aus Lexikon der Kunststoffprüfung
Zur Navigation springen Zur Suche springen
 
(28 dazwischenliegende Versionen von 6 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
−
<big>'''Adhäsive Energiefreisetzungsrate'''</big>
+
{{PSM_Infobox}}
 +
<span style="font-size:1.2em;font-weight:bold;">Adhäsive Energiefreisetzungsrate</span> (Autor: Prof. Dr. Michael Nase)
 +
__FORCETOC__
 +
==Allgemeines==
  
−
Die adhäsive Energiefreisetzungsrate G<sub>aIc</sub> spiegelt ausschließlich den Energieanteil wider, der für die Trennung zweier versiegelter Folien aufgewendet werden muss und ist bei elastisch-plastischem Werkstoffverhalten anwendbar.
+
Zur Charakterisierung des [[Peelverhalten – Modellierung|Peelverhaltens]] von Folien aus [[Kunststoffe|Kunststoff]] oder Metall, sowie Metall-Kunststoff-Verbunden stehen der [[T-Peeltest]] in Anlehnung an ASTM D 1876 "Standard Test Method for Peel Resistance of Adhesives (T-Peel-Test)" und der [[Fixed-Arm-Peeltest]] in Anlehnung an den ESIS TC4 Normvorschlag "Peel Testing of Flexible Laminates" zur Verfügung.
  
−
Die adhäsive Energiefreisetzungsrate G<sub>aIc</sub> wird nach Gl. 1 berechnet.
+
Für die werkstoffspezifische Beschreibung des [[Peelvorgang]]es werden die Methoden der [[Linear-elastische Bruchmechanik|linear-elastischen Bruchmechanik]] herangezogen, die es ermöglichen [[Werkstoffkenngröße|Kenngrößen]] mit einem hohen Informationsgehalt abzuleiten, wie z. B. die [[Energiefreisetzungsrate]]. Derartige Kenngrößen lassen sich dann vorteilhaft zur Bewertung des Einsatzverhaltens von Foliensystemen anwenden.
 +
 
 +
==Bewertung des Peelverhaltens gesiegelter Folien mit bruchmechanischen Kenngrößen==
 +
 
 +
Die adhäsive Energiefreisetzungsrate G<sub>aIc</sub> spiegelt ausschließlich den Energieanteil wider, der für die Trennung zweier versiegelter Folien (siehe: [[Siegelnaht]]) aufgewendet werden muss und ist bei elastisch-plastischem Werkstoffverhalten anwendbar.
 +
 
 +
Die adhäsive Energiefreisetzungsrate G<sub>aIc</sub> wird nach Gl. (1) berechnet.
 
{|
 
{|
 
|-
 
|-
−
!width="500px" | <math> G_{aIc} = \frac {U_a} { W L} = \frac {E_G-E_{d,P}-E_{Ed;S}}{W L}</math>
+
|width="20px"|
−
!width="100px" |(1)
+
|width="500px" | <math> G_{aIc} = \frac {U_a} { W L} = \frac {E_G-E_{d,P}-E_{d,S}}{W L}</math>
 +
|(1)
 +
|}
 +
 
 +
mit
 +
{|
 +
|-
 +
|U<sub>a</sub>
 +
|width="15px" |  
 +
|direkte Adhäsionsenergie<br>
 +
|-
 +
|E<sub>G</sub>
 +
|
 +
|Gesamtpeelenergie <br>
 +
|-
 +
|E<sub>d,P</sub>
 +
|
 +
|Deformationsenergie der Peelarme<br>
 
|-
 
|-
 +
|E<sub>d,S</sub>
 +
|
 +
|Deformationsenergie der gepeelten [[Siegelnaht]]<br>
 +
|-
 +
|W
 +
|
 +
|Breite der Siegelnaht<br>
 +
|-
 +
|L
 +
|
 +
|Länge der Siegelnaht
 
|}
 
|}
  
−
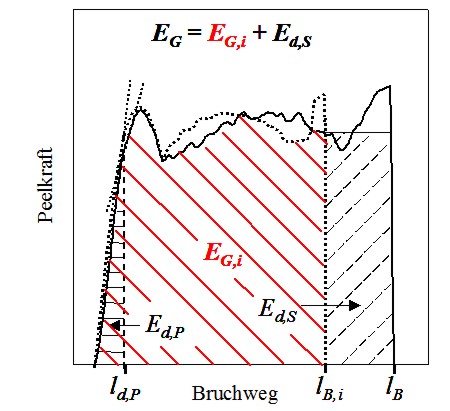
mit U<sub>a</sub> - direkte Adhäsionsenergie<br>
+
Die Gesamtpeelenergie E<sub>G</sub> entspricht dabei der Fläche unter dem [[Peelkraft-Bruchweg-Diagramm]] (auch Peelkurve; siehe '''Bild 1'''). Die Deformationsenergie der Peelarme E<sub>d,P</sub> ist die Energie, die vom Peelprüfkörper im Vorfeld des eigentlichen [[Peelvorgang]]s aufgenommen wird. Im [[Peelkraft-Bruchweg-Diagramm]] ist der Beginn des Peelvorgangs durch eine Änderung des Anstiegs der Peelkurve bei l<sub>d,P</sub> gekennzeichnet, so dass die Deformationsenergie der Peelarme E<sub>d,P</sub> der Fläche unter der Peelkurve bis l<sub>d,P</sub> entspricht. Es wird davon ausgegangen, dass sämtliche [[Deformation]]en, die nach l<sub>d,P</sub> infolge Krafterhöhung stattfinden, von der gepeelten Siegelnaht und nicht mehr vom Peelarm aufgenommen werden, da die gepeelte [[Siegelnaht]] eine größere Neigung zur Deformation aufweist als die Peelarme.   
−
E<sub>G</sub> - Gesamtpeelenergie <br>
 
−
E<sub>d,P</sub> - Deformationsenergie der Peelarme<br>
 
−
E<sub>d,S</sub> - Deformationsenergie der gepeelten Siegelnaht<br>
 
−
W - Breite der Siegelnaht<br>
 
−
L - Länge der Siegelnaht
 
−
 
 
−
 
 
−
Die Gesamtpeelenergie E<sub>G</sub> entspricht dabei der Fläche unter dem [[Peelkraft-Bruchweg-Diagramm]] (auch Peelkurve; siehe Bild 1). Die Deformationsenergie der Peelarme E<sub>d,P</sub> ist die Energie, die vom Peelprüfkörper im Vorfeld des eigentlichen [[Peelvorgang]]s aufgenommen wird. Im [[Peelkraft-Bruchweg-Diagramm]] ist der Beginn des Peelvorgangs durch eine Änderung des Anstiegs der Peelkurve bei l<sub>d,P</sub> gekennzeichnet, so dass die Deformationsenergie der Peelarme <sub>Ed,P</sub> der Fläche unter der Peelkurve bis l<sub>d,P</sub> entspricht. Es wird davon ausgegangen, dass sämtliche Deformationen, die nach l<sub>d,P</sub> infolge Krafterhöhung stattfinden, von der gepeelten Siegelnaht und nicht mehr vom Peelarm aufgenommen werden, da die gepeelte Siegelnaht eine größere Neigung zur Deformation aufweist als die Peelarme.   
 
  
 
[[Datei:adhesive_G_1.jpg]]
 
[[Datei:adhesive_G_1.jpg]]
 +
{|
 +
|- valign="top"
 +
|width="50px"|'''Bild 1''':
 +
|width="600px" |Darstellung des idealen Verlaufs der Peelkurve, d. h. ohne Deformation der Siegelnaht (gepunktete Kurve) im Vergleich zur realen Peelkurve (durchgehende Kurve); l<sub>d,P</sub> – Beginn des [[Peelvorgang]]s; l<sub>B</sub> – Bruchweg; l<sub>B,i</sub> – Bruchweg beim idealen Peelversuch; E<sub>d,P</sub> – Deformationsenergie der Peelarme; E<sub>d,S</sub> – Deformationsenergie der gepeelten [[Siegelnaht]] und E<sub>G,i</sub> – ideale Gesamtpeelenergie bei zugelassener Deformation des Peelarms
 +
|}
  
−
Bild 1: Darstellung des idealen Verlaufs der Peelkurve, d.h. ohne Deformation der Siegelnaht (gepunktete Kurve) im Vergleich zur realen Peelkurve (durchgehende Kurve); l<sub>d,P</sub> – Beginn des Peelvorgangs; l<sub>B</sub> – Bruchweg; l<sub>B,i</sub> – Bruchweg beim idealen Peelversuch; E<sub>d,P</sub> – Deformationsenergie der Peelarme;
+
Somit wird die Deformationsenergie der gepeelten [[Siegelnaht]] E<sub>d,S</sub> durch Subtraktion der idealen Gesamtpeelenergie E<sub>G,i</sub>, d. h. der Gesamtpeelenergie beim Vorhandensein einer idealen Siegelnaht mit unendlichem [[Elastizitätsmodul|E-Modul]] (gepunktete Peelkurve), von der Gesamtpeelenergie E<sub>G</sub> gemäß Gl. (2) berechnet. Es sei vorausgesetzt, dass der Peelarm auch beim Vorhandensein einer idealen [[Siegelnaht]] [[Deformation]]en aufnehmen kann.  
−
E<sub>d,S</sub> – Deformationsenergie der gepeelten Siegelnaht und E<sub>G,i</sub> – ideale Gesamtpeelenergie bei zugelassener Deformation des Peelarms
 
−
 
 
−
 
 
−
Somit wird die Deformationsenergie der gepeelten Siegelnaht E<sub>d,S</sub> durch Subtraktion der idealen Gesamtpeelenergie E<sub>G,i</sub>, d.h. der Gesamtpeelenergie beim Vorhandesein einer idealen Siegelnaht mit unendlichem E-Modul (gepunktete Peelkurve), von der Gesamtpeelenergie E<sub>G</sub> gemäß Gl. 2 berechnet. Es sei vorausgesetzt, dass der Peelarm auch beim Vorhandensein einer idealen Siegelnaht Deformationen aufnehmen kann.  
 
  
 
{|
 
{|
−
!width="500px" | <math> E_{d,S} = E_G\, -\, E_{G,i}</math>
 
−
!width=100px"|(2)\
 
 
|-
 
|-
 +
|width="20px"|
 +
|width="500px" | <math> E_{d,S} = E_G\, -\, E_{G,i}</math>
 +
|(2)
 
|}
 
|}
  
−
Es wird vorausgesetzt, dass die Deformationsenergie der gepeelten Siegelnaht E<sub>d,S</sub> nicht von der Deformationsenergie der Peelarme E<sub>d,P</sub> beeinflusst wird, so dass die beiden Deformationsprozesse, die Deformation der Peelarme und die Deformation der Siegelnaht, nacheinander erfolgen. Der exakte Zahlenwert der idealen Gesamtpeelenergie E<sub>G,i</sub> ist nicht berechenbar, dennoch kann die Deformationsenergie der gepeelten Siegelnaht E<sub>d,S</sub> nach Gl. 3 angenähert werden.
+
Es wird vorausgesetzt, dass die Deformationsenergie der gepeelten Siegelnaht E<sub>d,S</sub> nicht von der Deformationsenergie der Peelarme E<sub>d,P</sub> beeinflusst wird, so dass die beiden Deformationsprozesse, die Deformation der Peelarme und die Deformation der Siegelnaht, nacheinander erfolgen. Der exakte Zahlenwert der idealen Gesamtpeelenergie E<sub>G,i</sub> ist nicht berechenbar, dennoch kann die Deformationsenergie der gepeelten Siegelnaht E<sub>d,S</sub> nach Gl. (3) angenähert werden.
  
 
{|
 
{|
−
!width="500px" | <math> E_{d,S} = E_G - E_{G,i}\approx (l_B-L_{B,i})F_{peel}</math>
+
|width="20px"|
−
!width=100px"|(3)
+
|width="500px" | <math> E_{d,S} = E_G - E_{G,i}\approx (l_B-l_{B,i})F_{peel}</math>
−
|-
+
|(3)
 
|}
 
|}
  
−
mit l<sub>B</sub> - Bruchweg beim realen Peelversuch und l<sub>B,i</sub> - Bruchweg beim idealen Peelversuch, d.h. ohne Deformationen der gepeelten Siegelnaht  
+
mit  
 +
{|
 +
|-
 +
|l<sub>B</sub>
 +
|width="15px" |
 +
|Bruchweg beim realen Peelversuch<br>
 +
|-
 +
|l<sub>B,i</sub>
 +
|
 +
|Bruchweg beim idealen Peelversuch, d. h. ohne Deformationen der gepeelten Siegelnaht
 +
|} 
  
−
Der Bruchweg im idealen Peelversuch wird für den T-Peeltest nach Gl. 4 und für den Fixed-Arm Peeltest nach Gl. 5 berechnet.
+
Der Bruchweg im idealen [[Peeltest]] wird für den [[T-Peeltest]] nach Gl. (4) und für den [[Fixed-Arm-Peeltest]] nach Gl. (5) berechnet.
  
 
{|
 
{|
−
!width="500px" | <math> l_{B,i} = l_{d,P}\, +\, 2 W</math>
 
−
!width=100px"|(4)
 
 
|-
 
|-
 +
|width="20px"|
 +
|width="500px" | <math> l_{B,i} = l_{d,P}\, +\, 2 W</math>
 +
|(4)
 
|}
 
|}
 
   
 
   
−
mit l<sub>d,P</sub> Beginn des Peelvorgangs
+
mit
 +
{|
 +
|-
 +
|l<sub>d,P</sub>
 +
|width="15px" |
 +
|Beginn des [[Peelvorgang]]s
 +
|}
  
 
{|
 
{|
−
!width="500px" | <math> l_{B,i} = l_{d,P}\, +\, (W-W \cos \theta)</math>
 
−
!width=100px"|(5)
 
 
|-
 
|-
 +
|width="20px" |
 +
|width="500px" | <math> l_{B,i} = l_{d,P}\, +\, (W-W \cos \theta)</math>
 +
|(5)
 
|}
 
|}
−
(5)
 
  
−
mit <math>\theta</math> - Peelwinkel
+
mit  
 +
{|
 +
|-
 +
|<math>\theta</math>
 +
|width="15px" |
 +
|[[Peelwinkel]]
 +
|}
  
−
Beispielsweise wird die adhäsive Energiefreisetzungsrate beim Peelsystem Polyethylen niederer Dichte geblendet mit isotaktischem Polybuten-1 (PE-LD/iPB-1) maßgeblich durch die Blendzusammensetzung beeinflusst. Als Ergebnis des T-[[Peeltest]]s ist in Bild 2 die adhäsive Energiefreisetzungsrate in Abhängigkeit vom iPB-1-Gehalt dargestellt. Die adhäsive Energiefreisetzungsrate vermindert sich exponentiell mit zunehmendem iPB-1-Gehalt. Diese Abhängigkeit wird bei der gezielten Einstellung des PE-LD/iPB-1-Peelsystems unter Verwendung bruchmechanischer Kennwerte zugrunde gelegt.
+
==Anwendungsbeispiel für ein PE-LD/iPB-1-Peelsystem==
  
 +
Die adhäsive Energiefreisetzungsrate beim Peelsystem Polyethylen niederer Dichte geblendet mit isotaktischem Polybuten-1 ([[Kurzzeichen]]: PE-LD/iPB-1) wird maßgeblich durch die Blendzusammensetzung beeinflusst. Als Ergebnis des [[T-Peeltest]]s ist in '''Bild 2''' die adhäsive Energiefreisetzungsrate in Abhängigkeit vom iPB-1-Gehalt dargestellt. Die adhäsive Energiefreisetzungsrate vermindert sich exponentiell mit zunehmendem iPB-1-Gehalt. Diese Abhängigkeit wird bei der gezielten Einstellung des PE-LD/iPB-1-Peelsystems unter Verwendung bruchmechanischer Kennwerte (siehe: [[Bruchmechanische Prüfung]]) zugrunde gelegt.
  
−
[[Datei:ahaesive_G_2.jpg]]
+
[[Datei:ahaesive_G_2.jpg |400px]]
 +
{|
 +
|- valign="top"
 +
|width="50px"|'''Bild 2''':
 +
|width="600px" |Einfluss des Masseanteils an iPB-1 auf die adhäsive Energiefreisetzungsrate
 +
|}
  
−
Bild 2: Einfluss des Masseanteils an iPB-1 auf die adhäsive Energiefreisetzungsrate
+
==Siehe auch==
 +
*[[Peeleigenschaften von Peelsystemen]]
 +
*[[Fixed-Arm-Peeltest]]
 +
*[[T-Peeltest]]
 +
*[[Peelverhalten – Modellierung]]
  
  
 
'''Literaturhinweise'''
 
'''Literaturhinweise'''
−
 
+
* Kinloch, A. J., Lau, C. C, Williams, J. G.: The Peeling of Flexible Laminates. Intern. J. of Fracture 66 (1994) 45–70 DOI: [https://doi.org/10.1007/BF00012635 https://doi.org/10.1007/BF00012635]
−
{|
+
* Nase, M., Langer, B., Müller, C., [[Grellmann,_Wolfgang|Grellmann, W.]]: Bruchmechanische Kennwertermittlung im T-Peeltest und im Fixed-Arm Peeltest. In: Frenz, H., [https://www.researchgate.net/profile/Wolfgang-Grellmann Grellmann, W.] (Hrsg.): 26. Tagung Werkstoffprüfung „Herausforderung neuer Werkstoffe an die Forschung und Werkstoffprüfung“, Berlin (2008) Tagungsband S. 223–228, ISBN 978-3-00-026399-6 (siehe [[AMK-Büchersammlung]] unter A 10) [https://www.polymerservice-merseburg.de/fileadmin/inhalte/psm/veroeffentlichungen/Bruchmechanische_Kennwertermittlung_im_T_Peelttest_WP2008.pdf Download als pdf]
−
 
+
* Nase, M., Langer, B., Baumann, H. J., Grellmann, W.: Fracture Mechanics on Polyethylene/Polybutene-1 Peel Films. Polymer Testing 27 (2008) 1017–1025 DOI: [https://doi.org/10.1016/j.polymertesting.2008.09.002 https://doi.org/10.1016/j.polymertesting.2008.09.002]
−
|[1]
+
* Nase, M.: Charakterisierung von polymeren Peelsystemen durch Anwendung neuartiger Methoden der experimentellen Bruchmechanik. Habilitation, Otto-von Guericke-Universität Magdeburg, Shaker Verlag 2022 (ISBN 978-3-8440-8635-5; siehe [[AMK-Büchersammlung]] unter B 2-3),[https://www.polymerservice-merseburg.de/fileadmin/inhalte/psm/veroeffentlichungen/Nase_Habilitation_Inhaltsverzeichnis.pdf Inhaltsverzeichnis als pdf]
−
|Kinloch, A.J., Lau, C.C, Williams, J.G.: The peeling of flexible laminates. International Journal of Fracture, 66 (1994) 45–70
+
[[Kategorie:Folienprüfung]]
−
|-valign="top"
+
[[Kategorie:Peeltest]]
−
|[2]
+
[[Kategorie:Gastbeiträge]]
−
|Nase, M., Langer, B., Grellmann, W.: Bruchmechanische Kennwertermittlung im T-Peeltest und im Fixed-Arm Peeltest. In: Frenz, H., Grellmann, W. (Hrsg.) 26. Tagung Werkstoffprüfung „Herausforderung neuer Werkstoffe an die Forschung und Werkstoffprüfung“, Berlin (2008) Tagungsband S. 223–228, ISSN 1861-8154; ISBN 978-3-00-026399-6
 
−
|-valign="top"
 
−
|[3]
 
−
|Nase, M., Langer, B., Baumann, H.J., Grellmann, W.: Fracture mechanics on polyethylene/polybutene-1 peel films. Polymer Testing 27 (2008) 1017–1025
 
−
|
 
−
|}
 

Aktuelle Version vom 30. September 2024, 09:40 Uhr

Ein Service der
Logo psm.jpg
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50
E-Mail: info@psm-merseburg.de
Web: https://www.psm-merseburg.de
Unser Weiterbildungsangebot:
https://www.psm-merseburg.de/weiterbildung
PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Adhäsive Energiefreisetzungsrate (Autor: Prof. Dr. Michael Nase)

Allgemeines

Zur Charakterisierung des Peelverhaltens von Folien aus Kunststoff oder Metall, sowie Metall-Kunststoff-Verbunden stehen der T-Peeltest in Anlehnung an ASTM D 1876 "Standard Test Method for Peel Resistance of Adhesives (T-Peel-Test)" und der Fixed-Arm-Peeltest in Anlehnung an den ESIS TC4 Normvorschlag "Peel Testing of Flexible Laminates" zur Verfügung.

Für die werkstoffspezifische Beschreibung des Peelvorganges werden die Methoden der linear-elastischen Bruchmechanik herangezogen, die es ermöglichen Kenngrößen mit einem hohen Informationsgehalt abzuleiten, wie z. B. die Energiefreisetzungsrate. Derartige Kenngrößen lassen sich dann vorteilhaft zur Bewertung des Einsatzverhaltens von Foliensystemen anwenden.

Bewertung des Peelverhaltens gesiegelter Folien mit bruchmechanischen Kenngrößen

Die adhäsive Energiefreisetzungsrate GaIc spiegelt ausschließlich den Energieanteil wider, der für die Trennung zweier versiegelter Folien (siehe: Siegelnaht) aufgewendet werden muss und ist bei elastisch-plastischem Werkstoffverhalten anwendbar.

Die adhäsive Energiefreisetzungsrate GaIc wird nach Gl. (1) berechnet.

(1)

mit

Ua direkte Adhäsionsenergie
EG Gesamtpeelenergie
Ed,P Deformationsenergie der Peelarme
Ed,S Deformationsenergie der gepeelten Siegelnaht
W Breite der Siegelnaht
L Länge der Siegelnaht

Die Gesamtpeelenergie EG entspricht dabei der Fläche unter dem Peelkraft-Bruchweg-Diagramm (auch Peelkurve; siehe Bild 1). Die Deformationsenergie der Peelarme Ed,P ist die Energie, die vom Peelprüfkörper im Vorfeld des eigentlichen Peelvorgangs aufgenommen wird. Im Peelkraft-Bruchweg-Diagramm ist der Beginn des Peelvorgangs durch eine Änderung des Anstiegs der Peelkurve bei ld,P gekennzeichnet, so dass die Deformationsenergie der Peelarme Ed,P der Fläche unter der Peelkurve bis ld,P entspricht. Es wird davon ausgegangen, dass sämtliche Deformationen, die nach ld,P infolge Krafterhöhung stattfinden, von der gepeelten Siegelnaht und nicht mehr vom Peelarm aufgenommen werden, da die gepeelte Siegelnaht eine größere Neigung zur Deformation aufweist als die Peelarme.

Adhesive G 1.jpg

Bild 1: Darstellung des idealen Verlaufs der Peelkurve, d. h. ohne Deformation der Siegelnaht (gepunktete Kurve) im Vergleich zur realen Peelkurve (durchgehende Kurve); ld,P – Beginn des Peelvorgangs; lB – Bruchweg; lB,i – Bruchweg beim idealen Peelversuch; Ed,P – Deformationsenergie der Peelarme; Ed,S – Deformationsenergie der gepeelten Siegelnaht und EG,i – ideale Gesamtpeelenergie bei zugelassener Deformation des Peelarms

Somit wird die Deformationsenergie der gepeelten Siegelnaht Ed,S durch Subtraktion der idealen Gesamtpeelenergie EG,i, d. h. der Gesamtpeelenergie beim Vorhandensein einer idealen Siegelnaht mit unendlichem E-Modul (gepunktete Peelkurve), von der Gesamtpeelenergie EG gemäß Gl. (2) berechnet. Es sei vorausgesetzt, dass der Peelarm auch beim Vorhandensein einer idealen Siegelnaht Deformationen aufnehmen kann.

(2)

Es wird vorausgesetzt, dass die Deformationsenergie der gepeelten Siegelnaht Ed,S nicht von der Deformationsenergie der Peelarme Ed,P beeinflusst wird, so dass die beiden Deformationsprozesse, die Deformation der Peelarme und die Deformation der Siegelnaht, nacheinander erfolgen. Der exakte Zahlenwert der idealen Gesamtpeelenergie EG,i ist nicht berechenbar, dennoch kann die Deformationsenergie der gepeelten Siegelnaht Ed,S nach Gl. (3) angenähert werden.

(3)

mit

lB Bruchweg beim realen Peelversuch
lB,i Bruchweg beim idealen Peelversuch, d. h. ohne Deformationen der gepeelten Siegelnaht

Der Bruchweg im idealen Peeltest wird für den T-Peeltest nach Gl. (4) und für den Fixed-Arm-Peeltest nach Gl. (5) berechnet.

(4)

mit

ld,P Beginn des Peelvorgangs
(5)

mit

Peelwinkel

Anwendungsbeispiel für ein PE-LD/iPB-1-Peelsystem

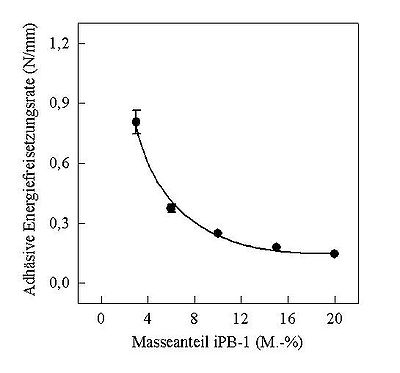
Die adhäsive Energiefreisetzungsrate beim Peelsystem Polyethylen niederer Dichte geblendet mit isotaktischem Polybuten-1 (Kurzzeichen: PE-LD/iPB-1) wird maßgeblich durch die Blendzusammensetzung beeinflusst. Als Ergebnis des T-Peeltests ist in Bild 2 die adhäsive Energiefreisetzungsrate in Abhängigkeit vom iPB-1-Gehalt dargestellt. Die adhäsive Energiefreisetzungsrate vermindert sich exponentiell mit zunehmendem iPB-1-Gehalt. Diese Abhängigkeit wird bei der gezielten Einstellung des PE-LD/iPB-1-Peelsystems unter Verwendung bruchmechanischer Kennwerte (siehe: Bruchmechanische Prüfung) zugrunde gelegt.

Ahaesive G 2.jpg

Bild 2: Einfluss des Masseanteils an iPB-1 auf die adhäsive Energiefreisetzungsrate

Siehe auch


Literaturhinweise

  • Kinloch, A. J., Lau, C. C, Williams, J. G.: The Peeling of Flexible Laminates. Intern. J. of Fracture 66 (1994) 45–70 DOI: https://doi.org/10.1007/BF00012635
  • Nase, M., Langer, B., Müller, C., Grellmann, W.: Bruchmechanische Kennwertermittlung im T-Peeltest und im Fixed-Arm Peeltest. In: Frenz, H., Grellmann, W. (Hrsg.): 26. Tagung Werkstoffprüfung „Herausforderung neuer Werkstoffe an die Forschung und Werkstoffprüfung“, Berlin (2008) Tagungsband S. 223–228, ISBN 978-3-00-026399-6 (siehe AMK-Büchersammlung unter A 10) Download als pdf
  • Nase, M., Langer, B., Baumann, H. J., Grellmann, W.: Fracture Mechanics on Polyethylene/Polybutene-1 Peel Films. Polymer Testing 27 (2008) 1017–1025 DOI: https://doi.org/10.1016/j.polymertesting.2008.09.002
  • Nase, M.: Charakterisierung von polymeren Peelsystemen durch Anwendung neuartiger Methoden der experimentellen Bruchmechanik. Habilitation, Otto-von Guericke-Universität Magdeburg, Shaker Verlag 2022 (ISBN 978-3-8440-8635-5; siehe AMK-Büchersammlung unter B 2-3),Inhaltsverzeichnis als pdf
Abgerufen von „https://wiki.polymerservice-merseburg.de/index.php?title=Adhäsive_Energiefreisetzungsrate&oldid=9287“