Farbabstand

Ein Service der
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung
PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Farbabstand

CIE-Farbunterschiedsmetrik, Farbabstandsgleichungen

Neben der Farbe ist eine wichtige und bestimmende Größe die Ermittlung der Farbveränderung bzw. die Änderung des Farbabstandes ΔE. Hierfür werden verschiedene mathematische Ansätze (Farbabstandsgleichungen) verwendet [1].

CIELAB-Farbabstand ΔE^*_ab und ΔE^*_Ch

Die größte Verbreitung besitzt dabei der CIELAB-Farbabstand $\Delta E_{ab}^{*}$ aus dem Jahr 1976 nach Gl. (1) und Gl (2). Jede gemessene Farbe wird durch drei Größen charakterisiert, welche sich in einem dreidimensionalen Raum als Vektoren beschreiben lassen. Der euklidische Abstand (Farbabstand $\Delta E_{ab}^{*}$) beschreibt die Länge bzw. Strecke, welche zwei Punkte verbindet und kann sowohl für das kartesische Gl. (1) wie auch für das Polarkoordinatensystem Gl. (2), erfolgen. Für eine bessere Unterscheidung wird abweichend von der in der Norm vorgegeben Nomenklatur $\Delta E_{ab}^{*}$ für die Gl. (2) stattdessen das Symbol $\Delta E_{Ch}^{*}$ verwendet.

$\Delta E_{ab}^{*}={\sqrt {(\Delta L^{*})^{2}+(\Delta a^{*})^{2}+(\Delta b^{*})^{2}}}$	(1)
$\Delta L^{*}=L_{1}^{*}-L_{0}^{*}$ = Helligkeits-Differenz
$\Delta a^{*}=a_{1}^{*}-a_{01}^{*}$ = Abstand Rot-Grün-Buntheit
$\Delta b^{*}=b_{1}^{*}-b_{0}^{*}$ = Abstand Gelb-Blau-Buntheit
$\Delta E_{ab}^{*}=\Delta E_{Ch}^{*}={\sqrt {(\Delta L^{*})^{2}+(\Delta C_{ab}^{*})^{2}+(\Delta H_{ab}^{*}*)^{2}}}$	(2)
$\Delta C_{ab}^{*}=\Delta C_{ab,1}^{*}-\Delta C_{ab,0}^{*}$ = Buntheit-Differenz
$\Delta H_{ab}^{*}=2\cdot {\sqrt {\Delta C_{ab,1}^{*}\cdot \Delta C_{ab,2}^{*}}}\cdot \sin({\frac {\Delta h_{ab}}{2}})$
$\Delta h_{ab}=\Delta h_{ab,1}-\Delta h_{ab,0}\!$ = Buntton-Differenz

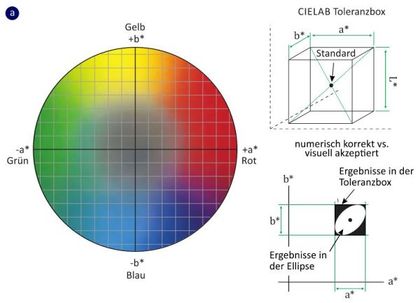
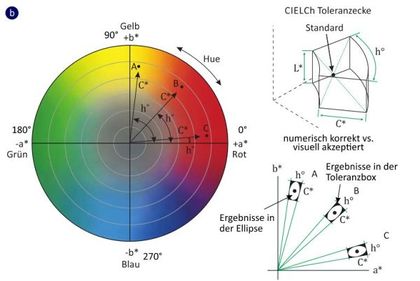
Der CIELAB-Farbraum ist allerdings nur annähernd gleichabständig, d. h., es wird nicht erreicht, dass die physiologische Wahrnehmung (ermittelt durch experimentelle Untersuchungen mit normalsichtigen Testpersonen [2]) von gerade noch wahrnehmbaren Farbdifferenzen für alle Farben im Raum gleich ist. Dies ist schematisch im Bild 1a für das kartesische und in Bild 1b für das polare Koordinatensystem dargestellt.

Die Darstellung der mathematischen Berechnung von Farbabständen nach Gl. (1) und Gl. (2) ist in Bild 1a und b jeweils durch die Toleranzbox bzw. die Toleranzecke gekennzeichnet. Dabei ist der Unterschied zwischen der visuelle Übereinstimmung und der mathematischen Berechnung durch die Farbe schwarz gekennzeichnet, d. h. es wird numerisch korrekt ein Wert berechnet, welcher allerdings nicht zu einem visuell wahrgenommen Farbunterschied führt. Diese Diskrepanz ist bei der Berechnung für das kartesische Koordinatensystem Gl. (1) größer, als bei der Berechnung nach Gl. (2) für das Polarkoordinatensystem. Weiterhin werden bei gesättigten Farben Farbdifferenzen geringer empfunden, als es zu erwarten wäre, so dass insbesondere Blautöne falsch bewertet werden. Ein weiteres Problem ist, dass geringe Farbabstände im CIELAB-Farbraum nur schlecht wiedergegeben werden und aus diesem Grund angepasste Farbabstandsformeln verwendet werden müssen [1].

Bild 1:

Schematische Darstellung der Berechnung der Farbtoleranzen für den CIELAB-Farbraum im kartesischen Koordinatensystem $\Delta E_{ab}^{*}$ (a) und für das Polarkoordinatensystem $\Delta E_{Ch}^{*}$ (b); in Anlehnung an [3]

CIELAB-Farbabstand ΔE^*_CMC

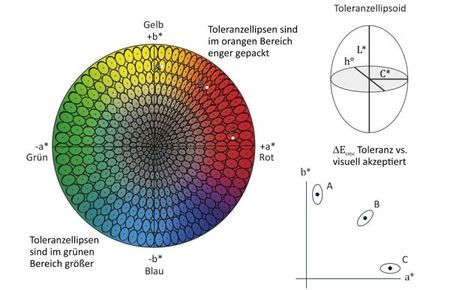
Die Farbabstandsformel $\Delta E_{ab}^{*}$ wurde gleich nach Veröffentlichung in der britischen Textilindustrie von McDonald [4‒6] durch umfangreiche Pass/Fail-Untersuchungen getestet und die genannten Unzulänglichkeiten konnten vollumfänglich bestätigt werden. Allerdings wurde im Rahmen der Untersuchungen ebenfalls festgestellt, dass gleiche Toleranzlimits in Form von in der Größe veränderbaren Ellipsen beschrieben werden können. Ausgehend von dem CIELAB-Farbraum wurden daher für die Farbabstandsformel in Gl. (2) (Polarkoordinatensystem) Gewichtsfunktionen für die drei Komponenten eingeführt. So hat das Colour Measurement Commitee (CMC) der Society of Dyers & Colourists Society, Bradford, West Yorkshire, UK (SDC) im Jahr 1984 eine eigene Farbabstandsformel – $\Delta E_{CMC}^{*}$ bzw. CMC(l:c) – nach Clark, McDonald und Rigg [7] definiert, welche 1995 zum ISO Standard für die Farbermittlung von Textilen erhoben wurde. Die Gl. (3) gibt den mathematischen Zusammenhang zwischen den Messwerten und dem Farbabstand an und Gl. (4) bis Gl. (7) beschreiben die Gewichtsfunktionen für die Helligkeit S_L, die Buntheit S_C und den Buntton S_H, mit welchen versucht wird, die nicht vorhandenen gleichabständigen Farbabstände im CIELAB-Farbraum anzupassen. Der Parameter S_L hängt dabei von der Helligkeit ab und reduziert den Effekt des zunehmenden Helligkeitsunterschieds für Werte von $L_{1}^{*}$ über 16. Die Gewichtsfunktion für die Buntheit S_C reduziert den Unterschied der Buntheit im a*, b*-Diagramm, wo mit zunehmender Buntheit die Größe der Ellipsen zunimmt (vgl. Bild 2). Die Gewichtsfunktion S_H ist dagegen deutlich komplexer. Mit dieser Funktion wird versucht, dem Umstand gerecht zu werden, dass Variationen im Winkel der Buntheit h_ab,1 und des Bunttons $C_{ab,1}^{*}$ generell größenabhängig vom Buntton und Unregelmäßigkeiten im Winkel der Buntheit sind. Dies resultiert in Toleranzellipsen, welche im orangen Bereich enger gepackt und im grünen Bereich größer sind. Dies ist im Bild 2 graphisch dargestellt.

$\Delta E_{CMC}={\sqrt {\left({\frac {\Delta L^{*}}{l\cdot S_{L}}}\right)^{2}+\left({\frac {\Delta C_{ab}^{*}}{c\cdot S_{C}}}\right)^{2}+\left({\frac {\Delta H_{ab}^{*}}{S_{H}}}\right)^{2}}}$	(3)
$S_{L}={\frac {0,040975\cdot L_{1}^{*}}{(1+0,01765\cdot L_{1}^{*})}}$ für $L_{1}^{*}$ ≥ 16	(4)
$S_{L}=0,511\!$ für $L_{1}^{*}$ < 16	(5)
$S_{C}={\frac {0,0638\cdot C_{ab,1}^{*}}{(1+0,0131\cdot C_{ab,1}^{*})}}+0,638$	(6)
$S_{H}=S_{C}\cdot (T\cdot f+1-f)$	(7)
$f={\sqrt {\frac {(C_{ab,1}^{*})^{4}}{(C_{ab,1}^{*})^{4}+1900}}}$	(8)
$T=0,56+\left|0,2\cdot \cos \cdot (h_{ab,1}+168)\right|$   gilt, falls hab,1 zwischen 164° und 345° liegt,	(9)
$T=0,36+\left|0,4\cdot \cos \cdot (h_{ab,1}+35)\right|$	(10)

Bild 2:

Schematische Darstellung der Berechnung der Farbtoleranzen für den CIELAB-Farbraum im Polarkoordinatensystem für die Farbabstandsgleichung $\Delta E_{CMC}^{*}$ ; in Anlehnung an [3]

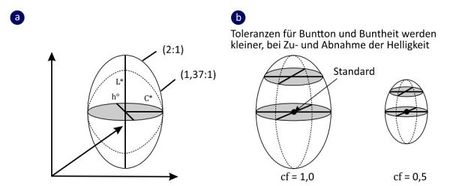
Die Parameter l und c in Gl. (3) sind linear abhängige Faktoren, welche die relative Empfindlichkeit zwischen den Helligkeits- und Buntheitsunterschieden festlegen. Das Auge reagiert prinzipiell empfindlicher auf Änderungen der Helligkeit (l) als auf Änderungen der Buntheit (c). Bei Abmusterungsuntersuchungen in der Textilindustrie wurde ein Verhältnis von l : c von 2 : 1 festgesetzt. Für Kunststoffe wird dagegen ein Verhältnis von 1,37 : 1 verwendet [8]. In Bild 3a sind schematisch die Ellipsoide für die genannten l : c-Verhältnisse dargestellt. Weiterhin wird in kommerziellen Situationen durch die Festlegung des „commercial factors cf“ die Größe des akzeptablen Farbunterschiedes auf alle Dimensionen der Ellipsoiden angepasst. Dies bedeutet, dass durch den cf-Faktor die Größe der Ellipsoiden so angepasst werden kann, dass es der visuellen Akzeptanz entspricht (Bild 3b). Ein cf-Wert von 1,0 bedeutet, dass bei Pass/Fail-Unter­suchungen $\Delta E_{CMC}^{*}$-Werte kleiner Eins akzeptiert und Werte größer Eins nicht akzeptiert werden.

Bild 3:

Schematische Darstellung unterschiedlicher l : c-Verhältnisse (a) sowie des commercial factors cf (b) [9]

CIELAB-Farbabstand ΔE^*₉₄ und ΔE^*₀₀

Die CIE hat ausgehend von den Unzulänglichkeiten der Farbabstandsformel CIELAB 1976 und den Ergebnisses von Clark, McDonald und Rigg [7] dagegen eigene Anstrengungen zur Verbesserung unternommen. So hat die CIE weitere Farbabstandsformeln in den Jahren 1994 und 2000 festgelegt, welche die Blautöne, den Einfluss der Umgebungshelligkeit, die Adaption an die Helligkeit sowie hellen und dunklen Töne besser berücksichtigen. Die Bestimmung des Farbabstandes $\Delta E_{94}^{*}$ (auch CIE94) nach Gl. (11) berücksichtigt ausgehend von den Ergebnissen von Clark, McDonald und Rigg [7] ebenso verschiedene Gewichtsfunktionen für die Helligkeit S_L Gl. (12), die Buntheit S_C Gl. (13) sowie den Buntton S_H Gl. (14).

$\Delta E_{94}^{*}={\sqrt {\left({\frac {\Delta L^{*}}{k_{L}\cdot S_{L}}}\right)^{2}+\left({\frac {\Delta C_{ab}^{*}}{k_{C}\cdot S_{C}}}\right)^{2}+\left({\frac {\Delta H_{ab}^{*}}{k_{H}\cdot S_{H}}}\right)^{2}}}$	(11)
$S_{L}=1\!$	(12)
$S_{C}=1+0,045\cdot C_{ab}^{*}$	(13)
$S_{H}=1+0,015\cdot C_{ab}^{*}$	(14)

Die Parameter k_L, k_C und k_H beschreiben die Differenz der experimentellen Bedingungen von den Referenzbedingungen, wie sie durch die CIE im Jahr 1993 für die Bestimmung von Farbabständen festgelegt wurden [10]:

• Beleuchtung mit Lichtart D65 (Normlichtart, Farbtemperatur 6503 K)
• Beleuchtungsstärke 1000 lx
• Umgebungsfarbe neutrales Grau mit L* gleich 50
• die Probengröße soll mehr als 4° des Gesichtsfeldes umfassen (10°-Normalbeobachter); (siehe Farbmetrik)
• Muster- und Vergleichsprobe sollten möglichst homogen und strukturlos sein
• Muster- und Vergleichsprobe sollen direkt nebeneinander liegend
• Größe des Farbabstandes $\Delta E_{ab}^{*}$ kleiner als 5

Werden die Messungen unter den Referenzbedingungen durchgeführt, gilt für alle Parameter der Zahlenwert 1. Abweichungen davon sind in entsprechender Weise durch eine geeignete Anpassung zu berücksichtigen. Eine Überprüfung der Farbabstandsformel durch umfangreiche Untersuchungen von Melgosa [11] sowie Rigg [12] ergaben, dass eine zusätzliche Gewichtsfunktion für die Helligkeit Gl. (12) nötig ist und insbesondere Abweichungen in dem gelben Bereich auftraten. Bezugnehmend auf Ergebnisse zur Festlegung der Farbabstandsformel CIE94 wurde umfangreiche neue Farbdatensätze [1] für weitere Untersuchungen festgelegt. Am Ende dieser Bemühungen stand die Farbabstandsformel $\Delta E_{00}^{*}$ (auch CIEDE2000) nach Gl. (30). Bei diesen Untersuchungen wurde eine Anpassung der Gewichtsfunktionen vorgenommen. Es wurde festgestellt, dass für unbunte Farben in der Nähe der b*-Achse die Kontur der Toleranzfunktion eine Ellipse und nicht wie erwartet ein Kreis ist. Dies machte die Definition eines neuen Koordinatensystems nötig, wo die nahen unbunten Ellipsen in Kreise entlang der a*-Achse transformiert werden. Hierfür wurden die Koordinaten a', b' und L' nach den Gleichungen (23) bis (27) festgelegt. Der Effekt der Transformation ist besonders für geringe Buntheitswerte gegeben und strebt für mittlere $C_{ab,m}^{*}$-Werte ab 30 den Wert Null an.

$a^{\prime }=a^{*}(1+G)\!$ mit	(15)
$G=0,5\cdot \left(1-{\sqrt {\frac {(C_{ab,m}^{*})^{7}}{(C_{ab,m}^{*})^{7}+25^{7}}}}\right)$	(16)
$C_{ab,m}^{*}={\frac {C_{ab,1}^{*}+C_{ab,2}^{*}}{2}}$	(17)
$b^{\prime }=b^{*}\!$	(18)
$L^{\prime }=L^{*}\!$	(19)

Die in der Farbabstandsformel $\Delta E_{94}^{*}$ nicht berücksichtigte Anpassung für die Helligkeit S_L gleich 1 wurde entsprechend der neuen Farbdatensätze und Untersuchungsergebnisse als nötig und von großem Einfluss erachtet [13], weshalb bei der CIEDE2000-Formel eine Funktion für S_L festgelegt wurde Gl. (20). Für die Gewichtsfunktion S_C gilt Gl. (22), welche den Effekt der Unterschiede in der Buntheit mit Zunahme der Buntheit beschreibt. Die Gewichtsfunktion für den Buntton S_H Gl. (24) ist dagegen komplexer, da ein komplizierter Zusammenhang zwischen den Unterschieden und den Bunttonwinkeln vorliegt [14]. Um diesen Umstand gerecht zu werden, wird die T-Funktion (Gl. 25) eingeführt. Eine weitere Schwierigkeit ist die Berücksichtigung der Blautöne im CIELAB-Farbraum, für welche bei den bisherig berücksichtigten Farbabstandsformeln nur unbefriedigende Ergebnisse erzielt wurden. Für eine adäquate Berücksichtigung wurde deshalb ein Rotationsterm R_T als multiplikative Funktion nach Gl. (27) festgelegt. Dieser Term nimmt entsprechend der Festlegung nur im blauen Bereich des CIELAB-Farbraumes mit Winkeln des Bunttons h_m von um 270° Werte größer Null an und hängt stark von der Buntheit C_m ab.

$S_{L}={\frac {1+0,015\cdot (L_{m}^{\prime }-50)^{2}}{\sqrt {20+(L_{m}^{\prime }-50)^{2}}}}$	(20)
$L_{m}^{\prime }={\frac {L_{1}^{\prime }+L_{0}^{\prime }}{2}}$	(21)
$S_{C}=1+0,045\cdot C_{m}$ mit	(22)
$C_{m}^{\prime }={\frac {C_{1}^{\prime }+C_{0}^{\prime }}{2}}$	(23)
$S_{H}=1+0,015\cdot C_{m}^{\prime }\cdot T$	(24)
$T=1-0,17\cdot \cos(h_{m}^{\prime }-30)+0,24\cdot \cos(2\cdot h_{m}^{\prime })+0,32\cdot \cos(3\cdot h_{m}^{\prime }+6)-0,20\cdot \cos(4\cdot h_{m}^{\prime }-63)$ mit	(25)
$h_{m}={\frac {h_{1}+h_{0}}{2}}$	(26)
$R_{T}=-\sin(2\Delta \Theta )\cdot R_{C}$ mit	(27)
$\Delta \Theta =30\cdot e^{\left({\frac {_{m}-275}{25}}\right)^{2}}$	(28)
$R_{C}=2\cdot {\sqrt {\frac {C_{m}^{\prime 7}}{C_{m}^{\prime \ 7}+25^{7}}}}$	(29)
$\Delta E_{00}={\sqrt {\left({\frac {\Delta L^{\prime }}{k_{L}\cdot S_{L}}}\right)^{2}+\left({\frac {\Delta C^{\prime }}{k_{C}\cdot S_{C}}}\right)^{2}+\left({\frac {\Delta H^{\prime }}{k_{H}\cdot S_{H}}}\right)^{2}+R_{T}\cdot \left({\frac {\Delta C^{\prime }}{k_{C}\cdot S_{C}}}\right)^{2}\cdot \left({\frac {\Delta H^{\prime }}{k_{H}\cdot S_{H}}}\right)^{2}}}$	(30)

Für die Parameter k_L, k_C und k_H gelten die gleichen Voraussetzungen wie für die CIE94-Formel und sie nehmen den Zahlenwert 1 an, wenn unter den Referenzbedingungen die Messungen durchgeführt wurden.

Ausgehend von den verschiedenen Farbabstandsformeln und umfangreichen Untersuchungen zur Anwendung und Übereinstimmung mit physiologischen Experimenten können die in Tabelle 1 aufgelisteten prozentualen visuellen Übereinstimmungen abgeleitet werden.

Tabelle 1:

Vergleich der visuellen und instrumentellen Ermittlung von Farbunterschieden [9, 15]

Toleranzmethode		visuelle Übereinstimmung
Formelzeichen	Abkürzung
$\Delta E_{ab}^{*}$	CIELAB 1976	75 %
$\Delta E_{ab}^{*}=\Delta E_{Ch}^{*}$	CIELAB 1976 / CIELCH 1976	85 %
$\Delta E_{CMC}\!$	CMC (l:c)	95 %
$\Delta E_{94}^{*}$	CIE94	95 %
$\Delta E_{00}\!$	CIEDE2000	> 95 %

Es ist ersichtlich, dass die visuelle Übereinstimmung im Bereich 75 % bis größer 95 % variiert und die besten Übereinstimmungen bei der CMC(l : c)- und der CIEDE2000-Farbabstandsformel vorliegen. Einen nachweisbarer Unterschied zwischen den CIE94- und CEDE2000-Formeln kann nicht eindeutig nachgewiesen werden und es wird aus diesem Grund von der CIE die Verwendung der Farbabstandsformel CIEDE2000-Formel als bevorzugt angesehen [1]. Entsprechend der Normungen für die Textilindustrie, ist die Verwendung der CMC(l : c)-Farbabstandsformel anzuwenden. Die Festlegung der für eigene Untersuchungen geeigneten Toleranzmethode kann unter Berücksichtigung der folgenden fünf Regeln nach Billmeyer (1970 und 1979) erfolgen [9]:

• Auswahl und Verwendung einer Toleranzmethode für alle Untersuchungen
• Exakte Angabe der Berechnung der Farbveränderung
• Niemals mit unterschiedlichen Methoden berechnete Farbunterschiede durch Verwendung von Durchschnitt-/Mittelwerten umrechnen
• Verwendung von Farbunterschieden nur als erste Annäherung bei der Festlegung von Toleranzen, außer sie werden durch eine visuelle Beurteilung bestätigt
• Niemand akzeptiert oder lehnt Farben aufgrund von Zahlen ab, es zählt nur das Aussehen.

Literaturhinweise

[1]	Witt, K.: CIE Color Difference Metrices. In: Schanda, J. (Ed.): Colorimetry: Understanding the CIE System. John Wiley & Sons, Inc., Hoboken, New Jersey (2007) 79–100
[2]	MacAdam, D. L.: Visual Sensitivities to Color Differences in Daylight. Journal of the Optical Society of America 32 (1942) 247–273
[3]	CIELAB – Color Management System, Document L10-281. X-Rite, Incorporated (2007)
[4]	McDonald, R.: Industrial Pass/Fail Colour Matching. Part III – Development of a Pass/Fail Formula for Use with Instrumental Measurement of Colour Difference. Journal of the Society of Dyers and Colourists 96 (1980) 486–497
[5]	McDonald, R.: Industrial Pass/Fail Colour Matching. Part II – Methods of Fitting Tolerance Ellipsoids. Journal of the Society of Dyers and Colourists 96 (1980) 418–433
[6]	McDonald, R.: Industrial Pass/Fail Colour Matching. Part 1 – Preparation of Visual Colour-Matching Data. Journal of the Society of Dyers and Colourists 96 (1980) 372–376
[7]	Clarke, F. J. J., McDonald, R., Rigg, B.: Modification to the JPC79 Colour-difference Formula. Journal of the Society of Dyers and Colourists 100 (1984) 128–132
[8]	A Guide to Understanding Color Tolerancing, Document L10-024. X-Rite, Incorporated (1997)
[9]	A Guide to Understanding Color Communication, Document L10-001. X-Rite, Incorporated (2007)
[10]	CIE Technical Report (1993): Parametric Effects in Colour-Difference Evaluation, CIE Publication 101
[11]	Melgosa, M., Hita, E., Pérez, M. M., El Moraghi, A.: Sensitivity Differences in Chroma, Hue, and Lightness from Several Classical Threshold Datasets. Color Research & Application 20 (1995) 220–225
[12]	Rigg, B.: Color Difference Formulae – Recent Developments. Journal of the Society of Dyers and Colourists 111 (1995) 267–271
[13]	Chou, W., Lin, H., Luo, M. R., Westland, S., Rigg, B., Nobbs, J.: Performance of Lightness Difference Formulae. Coloration Technology 117 (2001) 19–29
[14]	Luo, M. R., Cui, G., Rigg, B.: The Development of the CIE 2000 Colour-Difference Formula: CIEDE2000. Color Research & Application 26 (2001) 340‒350
[15]	Fundamentals Color & Appearance – A Practical Approach to Understanding and Managing Color Quality. X-Rite Pantone® (2015)