Oberflächenenergie: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (5 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Language_sel|LANG=eng|ARTIKEL=Surface Energy}} | |||
{{PSM_Infobox}} | {{PSM_Infobox}} | ||
<span style="font-size:1.2em;font-weight:bold;">Oberflächenenergie</span> | <span style="font-size:1.2em;font-weight:bold;">Oberflächenenergie</span> | ||
| Zeile 10: | Zeile 11: | ||
Die Oberflächen- bzw. Grenzflächenenergie ist bei [[Kunststoffe]]n besonders bei Lacken und Farben, Beschichtungen sowie Klebstoffen von wesentlicher Bedeutung. Sie ist aber auch dann von großem Interesse, wenn es allgemein um die Benetzbarkeit bzw. Nichtbenetzbarkeit von Kunststoffoberflächen geht. Ein Beispiel aus der Kunststoffindustrie sind Polyethylen-Folien, die der Verpackung wasserhaltiger Lebensmittel dienen. Bei diesen Folien kann sich das aus dem Lebensmittel stammende Wasser an der Folieninnenseite in Form kleiner Tröpfchen niederschlagen, was als Fogging bezeichnet wird. Durch gezielte Veränderung der Oberflächenenergie kann dieser Effekt unterdrückt werden, wodurch die Transparenz der Folien erhalten bleibt. | Die Oberflächen- bzw. Grenzflächenenergie ist bei [[Kunststoffe]]n besonders bei Lacken und Farben, Beschichtungen sowie Klebstoffen von wesentlicher Bedeutung. Sie ist aber auch dann von großem Interesse, wenn es allgemein um die Benetzbarkeit bzw. Nichtbenetzbarkeit von Kunststoffoberflächen geht. Ein Beispiel aus der Kunststoffindustrie sind Polyethylen-Folien, die der Verpackung wasserhaltiger Lebensmittel dienen. Bei diesen Folien kann sich das aus dem Lebensmittel stammende Wasser an der Folieninnenseite in Form kleiner Tröpfchen niederschlagen, was als Fogging bezeichnet wird. Durch gezielte Veränderung der Oberflächenenergie kann dieser Effekt unterdrückt werden, wodurch die Transparenz der Folien erhalten bleibt. | ||
Oft wird unter der spezifischen Grenzflächenenergie von Festkörpern der Betrag derjenigen Arbeit verstanden, der mindestens notwendig ist, neue Oberflächen (z. B. durch [[Rissausbreitung|Risswachstum]] und [[Bruch]]) zu schaffen. Auf dieser Grundlage basiert das Griffith-Kriterium der Bruchmechanik. Allerdings hat es sich gezeigt, dass diese bruchmechanisch ermittelten Werte (siehe: [[Bruchmechanische Prüfung]]) nur bei extrem spröden Werkstoffen (z. B. Si-Einkristallen) in der Größenordnung der mit anderen Verfahren ermittelten Werte liegen. Auch für spröde Kunststoffe und sehr tiefe Temperaturen (< –150 °C) sind die so ermittelten Werte, wie kritische J-Werte J<sub>c</sub>, um ca. vier bis fünf Größenordnungen größer. Für [[Thermoplaste|thermoplastische]] Kunststoffe umfassen sie den Bereich einiger kJ/m<sup>2</sup> (für amorphe Thermoplaste wie z. B. Polycarbonat ([[Kurzzeichen]]: PC), Polymethylmethacrylat ([[Kurzzeichen]]: PMMA) und Polystyren ([[Kurzzeichen]]: PS), ist J<sub>c</sub> = 1,0…1,8 kJ/m<sup>2</sup> [1, 2]). Diese Diskrepanz kann außer durch die in diesen Werkstoffen auch bei sehr tiefen Temperaturen auftretenden (mikro)plastischen [[Deformation|Deformationsprozesse]] (innere Energie) ebenfalls durch die Wärmetönung begründet werden, d. h. durch die Erzeugung von Wärme infolge innerer Reibungsvorgänge bei den mit der Erschaffung neuer Oberflächen (siehe: [[Bruchfläche]]) verbundenen Deformationsvorgängen. Der ideale Sprödbruch (siehe: [[Brucharten]]) ist dagegen ein athermischer Prozess. | Oft wird unter der spezifischen Grenzflächenenergie von Festkörpern der Betrag derjenigen Arbeit verstanden, der mindestens notwendig ist, neue Oberflächen (z. B. durch [[Rissausbreitung|Risswachstum]] und [[Bruch]]) zu schaffen. Auf dieser Grundlage basiert das [[GRIFFITH-Kriterium|Griffith-Kriterium]] der [[Bruchmechanik]]. Allerdings hat es sich gezeigt, dass diese bruchmechanisch ermittelten Werte (siehe: [[Bruchmechanische Prüfung]]) nur bei extrem spröden Werkstoffen (z. B. Si-Einkristallen) in der Größenordnung der mit anderen Verfahren ermittelten Werte liegen. Auch für spröde Kunststoffe und sehr tiefe Temperaturen (< –150 °C) sind die so ermittelten Werte, wie kritische J-Werte J<sub>c</sub>, um ca. vier bis fünf Größenordnungen größer. Für [[Thermoplaste|thermoplastische]] Kunststoffe umfassen sie den Bereich einiger kJ/m<sup>2</sup> (für amorphe Thermoplaste wie z. B. Polycarbonat ([[Kurzzeichen]]: PC), Polymethylmethacrylat ([[Kurzzeichen]]: PMMA) und Polystyren ([[Kurzzeichen]]: PS), ist J<sub>c</sub> = 1,0…1,8 kJ/m<sup>2</sup> [1, 2]). Diese Diskrepanz kann außer durch die in diesen Werkstoffen auch bei sehr tiefen Temperaturen auftretenden (mikro)plastischen [[Deformation|Deformationsprozesse]] (innere Energie) ebenfalls durch die Wärmetönung begründet werden, d. h. durch die Erzeugung von Wärme infolge innerer Reibungsvorgänge bei den mit der Erschaffung neuer Oberflächen (siehe: [[Bruchfläche]]) verbundenen Deformationsvorgängen. Der ideale Sprödbruch (siehe: [[Brucharten]]) ist dagegen ein athermischer Prozess. | ||
==Messung der Oberflächenenergie== | ==Messung der Oberflächenenergie== | ||
| Zeile 76: | Zeile 77: | ||
{| | {| | ||
|- valign="top" | |- valign="top" | ||
|width="550px"|<math>W=2\left ( \sqrt{\sigma_{l}^{p} | |width="550px"|<math>W=2\left ( \sqrt{\sigma_{l}^{p} \sigma_{s}^{p}}+\sqrt{\sigma_{l}^{d}\sigma_{s}^{d}} \right )</math> | ||
|width="50px"|(4) | |width="50px"|(4) | ||
|} | |} | ||
| Zeile 260: | Zeile 261: | ||
Kunststoffe mit einer geringen Oberflächenenergie und/oder unpolare Kunststoffe, zu denen z. B. polyolefine Werkstoffen allgemein, wie Polyethylen ([[Kurzzeichen]]: PE) und Polypropylen ([[Kurzzeichen]]: PP), sowie Kunststoffe auf der Basis von Polytetrafluorethylen ([[Kurzzeichen]]: PTFE) gehören (vgl. '''Tabelle 1'''), werden für Antihaftbeschichtungen (PTFE und dessen Copolymerisate, wie Perfluor-Tetrafluorethylen (PFA)), in der Lebensmittelindustrie (besonders PE) sowie für Rohre und Behälter (PE und PP) eingesetzt. Aufgrund der geringen Oberflächenenergie bzw. des geringen polaren Anteils der Oberflächenenergie sind sie allerdings ohne spezielle Oberflächenvorbehandlung nur schwer bedruckbar. | Kunststoffe mit einer geringen Oberflächenenergie und/oder unpolare Kunststoffe, zu denen z. B. polyolefine Werkstoffen allgemein, wie Polyethylen ([[Kurzzeichen]]: PE) und Polypropylen ([[Kurzzeichen]]: PP), sowie Kunststoffe auf der Basis von Polytetrafluorethylen ([[Kurzzeichen]]: PTFE) gehören (vgl. '''Tabelle 1'''), werden für Antihaftbeschichtungen (PTFE und dessen Copolymerisate, wie Perfluor-Tetrafluorethylen (PFA)), in der Lebensmittelindustrie (besonders PE) sowie für Rohre und Behälter (PE und PP) eingesetzt. Aufgrund der geringen Oberflächenenergie bzw. des geringen polaren Anteils der Oberflächenenergie sind sie allerdings ohne spezielle Oberflächenvorbehandlung nur schwer bedruckbar. | ||
==Siehe auch== | |||
*[[Bruch]] | |||
*[[Bruchentstehung]] | |||
*[[GRIFFITH-Kriterium]] | |||
*[[Energiefreisetzungsrate]] | |||
*[[Oberflächenprüftechnik]] | |||
| Zeile 267: | Zeile 276: | ||
|-valign="top" | |-valign="top" | ||
|[1] | |[1] | ||
|Lach, R.: Korrelationen zwischen bruchmechanischen Werkstoffkenngrößen und molekularen Relaxationsprozessen amorpher Polymere. VDI-Fortschritt-Berichte, Reihe 18: Mechanik/Bruchmechanik, Nr. 223, VDI-Verlag, Düsseldorf (1998) (ISBN 3- | |[https://researchgate.net/profile/Ralf-Lach Lach, R.]: Korrelationen zwischen bruchmechanischen Werkstoffkenngrößen und molekularen Relaxationsprozessen amorpher Polymere. VDI-Fortschritt-Berichte, Reihe 18: Mechanik/Bruchmechanik, Nr. 223, VDI-Verlag, Düsseldorf (1998) (ISBN 3-18-322318-x; siehe: [[AMK-Büchersammlung]] unter B 1-7) | ||
|-valign="top" | |-valign="top" | ||
|[2] | |[2] | ||
| Zeile 273: | Zeile 282: | ||
|-valign="top" | |-valign="top" | ||
|[3] | |[3] | ||
|Kopczynska, A., Ehrenstein, G. W.: Oberflächenspannung von Kunststoffen. Messmethoden am LKT. Sonderdrucke am Lehrstuhl für Kunststofftechnik, Friedrich-Alexander-Universität Erlangen-Nürnberg, siehe: [https://www.lkt.tf.fau.de/files/2017/06/Oberflaechenspannung.pdf https://www.lkt.tf.fau.de/files/2017/06/Oberflaechenspannung.pdf] (Zugriff am | |Kopczynska, A., [[Ehrenstein,_Gottfried_W.|Ehrenstein, G. W.]]: Oberflächenspannung von Kunststoffen. Messmethoden am LKT. Sonderdrucke am Lehrstuhl für Kunststofftechnik, Friedrich-Alexander-Universität Erlangen-Nürnberg, siehe: [https://www.lkt.tf.fau.de/files/2017/06/Oberflaechenspannung.pdf https://www.lkt.tf.fau.de/files/2017/06/Oberflaechenspannung.pdf] (Zugriff am 07.08.2023) und Kopczynska, A.: Oberflächenspannung. in: Ehrenstein, G. W.: Strukturverhalten. Struktur und Eigenschaften von Kunststoffen, Oberflächenspannung, Spannungsrisse. Carl Hanser Verlag München (2021), (ISBN 978-3-446-46703-3; siehe [[AMK-Büchersammlung]] unter F 25) | ||
|-valign="top" | |-valign="top" | ||
|[4] | |[4] | ||
Aktuelle Version vom 8. Januar 2026, 14:42 Uhr
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Oberflächenenergie
Grundlagen
Die Oberflächenenergie – oft auch als so genannte Oberflächenspannung bezeichnet, obwohl nicht von der Dimension Pascal – ist eine Materialeigenschaft. Im Allgemeinen wird als Oberflächenenergie die freie Energie von Oberflächen bei Temperaturen oberhalb des absoluten Nullpunktes definiert.
Genau genommen müsste der Begriff „Oberflächenenergie“ allerdings grundsätzlich auf den Begriff „Grenzflächenenergie“ erweitert werden, wird doch die eigentliche Oberflächenenergie, also die freie Energie einer flüssigen oder festen Oberfläche gegen ein Vakuum, nur in sehr seltenen Fällen damit erfasst. Zumeist sind daher relative Energiewerte der Grenzflächen von Flüssigkeiten zu anderen Flüssigkeiten bzw. Gasen/Dämpfen oder Grenzflächen von festen Stoffen zu anderen Stoffen, die als Feststoffe (innere Grenzflächen), Flüssigkeiten bzw. Gase/Dämpfe vorliegen, darunter zusammengefasst. Die Grenzflächenenergie ist deshalb keine Materialeigenschaft, sondern charakterisiert die Eigenschaft eines Stoffsystems und ist demzufolge also eine Systemeigenschaft.
Die Oberflächen- bzw. Grenzflächenenergie ist bei Kunststoffen besonders bei Lacken und Farben, Beschichtungen sowie Klebstoffen von wesentlicher Bedeutung. Sie ist aber auch dann von großem Interesse, wenn es allgemein um die Benetzbarkeit bzw. Nichtbenetzbarkeit von Kunststoffoberflächen geht. Ein Beispiel aus der Kunststoffindustrie sind Polyethylen-Folien, die der Verpackung wasserhaltiger Lebensmittel dienen. Bei diesen Folien kann sich das aus dem Lebensmittel stammende Wasser an der Folieninnenseite in Form kleiner Tröpfchen niederschlagen, was als Fogging bezeichnet wird. Durch gezielte Veränderung der Oberflächenenergie kann dieser Effekt unterdrückt werden, wodurch die Transparenz der Folien erhalten bleibt.
Oft wird unter der spezifischen Grenzflächenenergie von Festkörpern der Betrag derjenigen Arbeit verstanden, der mindestens notwendig ist, neue Oberflächen (z. B. durch Risswachstum und Bruch) zu schaffen. Auf dieser Grundlage basiert das Griffith-Kriterium der Bruchmechanik. Allerdings hat es sich gezeigt, dass diese bruchmechanisch ermittelten Werte (siehe: Bruchmechanische Prüfung) nur bei extrem spröden Werkstoffen (z. B. Si-Einkristallen) in der Größenordnung der mit anderen Verfahren ermittelten Werte liegen. Auch für spröde Kunststoffe und sehr tiefe Temperaturen (< –150 °C) sind die so ermittelten Werte, wie kritische J-Werte Jc, um ca. vier bis fünf Größenordnungen größer. Für thermoplastische Kunststoffe umfassen sie den Bereich einiger kJ/m2 (für amorphe Thermoplaste wie z. B. Polycarbonat (Kurzzeichen: PC), Polymethylmethacrylat (Kurzzeichen: PMMA) und Polystyren (Kurzzeichen: PS), ist Jc = 1,0…1,8 kJ/m2 [1, 2]). Diese Diskrepanz kann außer durch die in diesen Werkstoffen auch bei sehr tiefen Temperaturen auftretenden (mikro)plastischen Deformationsprozesse (innere Energie) ebenfalls durch die Wärmetönung begründet werden, d. h. durch die Erzeugung von Wärme infolge innerer Reibungsvorgänge bei den mit der Erschaffung neuer Oberflächen (siehe: Bruchfläche) verbundenen Deformationsvorgängen. Der ideale Sprödbruch (siehe: Brucharten) ist dagegen ein athermischer Prozess.
Messung der Oberflächenenergie
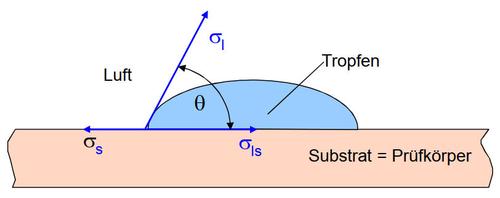
Die Grenzflächenenergie einer Kunststoffoberfläche gegen ein flüssiges Medium (oft Wasser) und zumeist Luft wird mittels der Kontaktwinkelmessung (Methode des liegenden Tropfens) ermittelt (Bild 1). Dazu wird auf einer ebenen und zuvor gründlich gereinigten Kunststoffoberfläche ein wohl definierter Flüssigkeitstropfen abgesetzt. Mit einer speziellen experimentellen Vorrichtung kann dann der Kontaktwinkel computergesteuert bestimmt werden (für Details der experimentellen Vorgehensweise siehe z. B. [3]).
| Bild 1: | Grenzflächenenergien am Dreiphasenkontakt: σs – Festkörperoberflächenenergie, σl – Flüssigkeitsoberflächenenergie, σls – Grenzflächenenergie, Θ – Rand- oder Kontaktwinkel |
Die Grenzflächenenergie wird durch die Gleichung (1) von Young [4] ermittelt, wobei der Einfluss des gasförmigen Mediums (wie Luft) vernachlässigt wird (daher werden σs und σl hier als Oberflächenenergie bezeichnet).
| (1) |
| mit: | ||
| σs | – | Festkörperoberflächenenergie (mJ/m2) |
| σl | – | Flüssigkeitsoberflächenenergie (mJ/m2) |
| σls | – | Grenzflächenenergie (mJ/m2) |
| Θ | – | Rand- oder Kontaktwinkel (Grad); die Benetzbarkeit nimmt mit zunehmendem Winkel ab |
Weiterhin kann durch Hinzuziehung von Gl. (1) die zur Ablösung eines Tropfens von einem Festkörper pro Fläche notwendige Arbeit W entsprechend der YOUNG-DUPRÉ-Gleichung (2) berechnet werden [5].
| (2) |
Dabei wird berücksichtigt, dass zwei neue Grenzflächen (Flüssigkeit gegen Luft und Festkörper gegen Luft) entstehen, während die Grenzfläche flüssig/fest verschwindet.
Anderseits wurde von Girifalco und Good [6] gefunden, dass sich die Ablösearbeit W näherungsweise in Form des geometrischen Mittels der Oberflächenenergien von Flüssigkeit und Festkörper (σs und σl) mittels Gl. (3) ausdrücken lässt.
| (3) |
Durch die Verwendung unterschiedlicher Referenz-Flüssigkeiten können mit dieser Methode auch der polare σlsp und der disperse Anteil σlsd der Grenzflächenenergie bestimmt werden. Hierbei sind die zur Grenzflächenenergie beitragenden polaren Wechselwirkungen die KEESOM-Wechselwirkung [7] zwischen zwei Dipolen und die DEBYE-Wechselwirkung [8] zwischen einem Dipol und einem polarisierbaren Molekül zu beachten. Der disperse Anteil der Wechselwirkung, der zur Grenzflächenenergie beiträgt, entsteht durch die Kräfte infolge der Londonsche Wechselwirkung [9] zwischen zwei polarisierbaren Molekülen. Alle drei Wechselwirkungen tragen zu den van-der-Waals-Kräften [10] bei.
Die beiden Wechselwirkungsarten (polar und dispers) tragen nun, da sie unabhängig voneinander sind, additiv zur Größe von W bei. Mit Gl. (3) ergibt sich somit die Gl. (4) (p und d stehen für polar und dispers):
| (4) |
Diese Additivität gilt ebenfalls für die Oberflächenenergien von Flüssigkeit und Festkörper. Mit der nach Einsetzen von Gl. (4) in Gl. (2) und Umformung enthaltenen Beziehung (5)
| (5) |
nach Owens, Wendt, Rabel und Kaelble (OWRK-Methode) [11–13] lässt sich nun die polare und disperse (und somit auch die gesamte) Oberflächenenergie eines Festkörpers ermitteln. Dazu wird mittels mehrerer Flüssigkeiten mit bekannter polarer und disperser Oberflächenenergie der Kontaktwinkel gemessen. Durch Auftragung von als Funktion von ergibt sich der polare Anteil der Festkörperoberflächenenergie als Anstieg der resultierenden Geraden und der disperse Anteil als Schnittpunkt mit der y-Achse.
Ein anderes für polymere Werkstoffe angewandtes Verfahren zur Ermittlung des polaren und dispersen Anteils der Oberflächenenergie ist die Methode nach Wu [14] mittels Gl. (6).
| (6) |
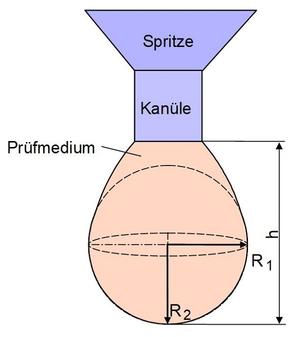
| Bild 2: | Methode des hängenden Tropfens: R1, R2 – Hauptkrümmungsradien, h – vertikale Höhe des Tropfens |
Zur Ermittlung der Oberflächenenergie einer Kunststoffschmelze (oder Lösung) wird die Methode des hängenden Tropfens verwendet (Bild 2). Hierbei wird die Oberflächenenergie aus der Kontur eines hängenden Tropfens bestimmt, der mittels einer Spritze dosiert wird. Die Form des sich am unteren Ende der Dosiernadel bildenden Tropfens lässt sich (bei Vernachlässigung des Einflusses des umgebenden Gases) entsprechend der YOUNG-LAPLACE-Gleichung [4, 15] durch das Kräftegleichgewicht zwischen Schwerkraft und Oberflächenenergie mathematisch exakt nach Gl. (7) beschreiben (für Details der experimentellen Vorgehensweise siehe z. B. [3]):
| (7) |
| mit: | ||
| σl | – | Flüssigkeitsoberflächenenergie (mJ/m2) |
| R1, R2 | – | Hauptkrümmungsradien (m) |
| ρ | – | Dichte der Flüssigkeit (g/m3) |
| g | – | Erdbeschleunigung (m/s2) |
| h | – | vertikale Höhe des Tropfens (m) |
Oberflächenenergien für ausgewählte Polymerwerkstoffe
In Tabelle 1 sind für ausgewählte Polymerwerkstoffe die Werte der Oberflächenenergie zusammengefasst. Typischerweise liegen diese Werte im Bereich von etwa 20… 50 mJ/m2.
| Werkstoff | Disperser Anteil der Oberflächenenergie (mJ/m2) | Polarer Anteil der Oberflächenenergie (mJ/m2) | Gesamte Oberflächenenergie (mJ/m2) |
|---|---|---|---|
| Epoxidharz | 19,5 | 13,2 | 32,7 |
| PA6 | 25,6...39,2 | 5,0...15,4 | 38,3...54,6 |
| PAEK | 36,0 | 3,8 | 39,8 |
| PBT | 39,4...41,8 | 3,3...9,4 | 43,8...48,8 |
| PC | 27,3...37,0 | 1,8...6,0 | 33,3...38,8 |
| PE-HD | 30,0...35,0 | 0,0...0,7 | 30,3...35,7 |
| PE-LD | 33,2...35,1 | 0,0 | 33,2...35,1 |
| PES | 42,1 | 5,1 | 47,2 |
| PET | 32,9...43,2 | 3,1...4,5 | 37,3...47,3 |
| PFA | 19,1 | 3,4 | 22,5 |
| PMMA | 25,7...44,2 | 4,3...14,6 | 40,2...51,3 |
| POM | 36,0...42,2 | 5,1...11,1 | 42,1...47,9 |
| PP | 25,8...42,1 | 0,3...1,3 | 31,2...42,4 |
| PPE | 42,7...44,7 | 2,1...3,2 | 45,9...46,8 |
| PS | 23,3...44,6 | 0,6...6,9 | 29,0...45,4 |
| PSU | 42,1 | 4,2 | 46,3 |
| PTFE | 18,5...18,6 | 0,0...0,5 | 18,5...19,1 |
| PVB | 36,0 | 4,7 | 40,7 |
| PVC | 26,0...40,0 | 1,5...12,7 | 37,3...51,7 |
| SAN | 27,1...42,1 | 2,7...7,7 | 31,1...47,2 |
| TPU | 35,2 | 3,8 | 39,0 |
PA6 – Polyamid 6, PAEK – Polyaryletherketon, PBT – Polybutylenterephthalat, PC – Polycarbonat, PE-HD – Polyethylen hoher Dichte, PE-LD – Polyethylen niedriger Dichte, PES – Polyethersulfon, PET – Polyethylenterephthalat, PFA – PTFE-Copolymerisat, PMMA – Polymethylmethacrylat, POM – Polyoxymethylen, PP – Polypropylen, PPE – Polyphenylenether, PS – Polystyren, PSU – Polysulfon, PTFE – Polytetrafluorethylen, PVB – Polybutylvinylbutyrat, PVC – Polyvinylchlorid, SAN – Styren-Acrylnitril-Copolymer, TPU – Thermoplastisches Polyurethan.
Wenn der polare Anteil der Oberflächenenergie größer als 1 mJ/m2 ist, dann spricht man von polaren Kunststoffen, ist er kleiner, von unpolaren Kunststoffen [16].
Kunststoffe mit einer geringen Oberflächenenergie und/oder unpolare Kunststoffe, zu denen z. B. polyolefine Werkstoffen allgemein, wie Polyethylen (Kurzzeichen: PE) und Polypropylen (Kurzzeichen: PP), sowie Kunststoffe auf der Basis von Polytetrafluorethylen (Kurzzeichen: PTFE) gehören (vgl. Tabelle 1), werden für Antihaftbeschichtungen (PTFE und dessen Copolymerisate, wie Perfluor-Tetrafluorethylen (PFA)), in der Lebensmittelindustrie (besonders PE) sowie für Rohre und Behälter (PE und PP) eingesetzt. Aufgrund der geringen Oberflächenenergie bzw. des geringen polaren Anteils der Oberflächenenergie sind sie allerdings ohne spezielle Oberflächenvorbehandlung nur schwer bedruckbar.
Siehe auch
Literaturhinweise
| [1] | Lach, R.: Korrelationen zwischen bruchmechanischen Werkstoffkenngrößen und molekularen Relaxationsprozessen amorpher Polymere. VDI-Fortschritt-Berichte, Reihe 18: Mechanik/Bruchmechanik, Nr. 223, VDI-Verlag, Düsseldorf (1998) (ISBN 3-18-322318-x; siehe: AMK-Büchersammlung unter B 1-7) |
| [2] | Hartwig, G., Saatkamp, T.: Fracture Properties of Polymers at Cryogenic Temperatures. Advances in Cryogenic Engineering 40 (1994) 1121–1127 |
| [3] | Kopczynska, A., Ehrenstein, G. W.: Oberflächenspannung von Kunststoffen. Messmethoden am LKT. Sonderdrucke am Lehrstuhl für Kunststofftechnik, Friedrich-Alexander-Universität Erlangen-Nürnberg, siehe: https://www.lkt.tf.fau.de/files/2017/06/Oberflaechenspannung.pdf (Zugriff am 07.08.2023) und Kopczynska, A.: Oberflächenspannung. in: Ehrenstein, G. W.: Strukturverhalten. Struktur und Eigenschaften von Kunststoffen, Oberflächenspannung, Spannungsrisse. Carl Hanser Verlag München (2021), (ISBN 978-3-446-46703-3; siehe AMK-Büchersammlung unter F 25) |
| [4] | Young, T.: An Essay on the Cohesion of Fluids. Philosophical Transactions of the Royal Society of London 95 (1805) 65–87 |
| [5] | Dupré, A., Dupré, P.: Théorie Mécanique de la Chaleur. Gauthier-Villars, Paris (1869) |
| [6] | Girifalco, L. A., Good, R. J.: A Theory for the Estimation of Surface and Interfacial Energies. I. Derivation and application to interfacial tension. The Journal of Physical Chemistry 61 (1957) 904–909 |
| [7] | Keesom, W. H.: The Second Virial Coefficient for Rigid Spherical Molecules whose Mutual Attraction is Equivalent to that of a Quadruplet Placed at its Center. Proceedings of the Royal Netherlands Academy of Arts and Sciences 18 (1915) 636–646 |
| [8] | Debye, P.: Polare Molekeln. S. Hirzel Verlag, Leipzig (1929) |
| [9] | London, F.: The General Theory of Molecular Forces. Transactions of the Faraday Society 33 (1937) 8–26 |
| [10] | van der Waals, J. D.: Over de Continuïteit van den Gas- en Vloeistoftoestand. Dissertation, Universität Leiden (1873) |
| [11] | Kaelble, D. H.: Dispersion-polar Surface Tension Properties of Organic Solids. The Journal of Adhesion 2 (1970) 66–81 |
| [12] | Owens, D., Wendt, R.: Estimation of the Surface Free Energy of Polymers. Journal of Applied Polymer Science 13 (1969) 1741–1747 |
| [13] | Rabel, W.: Einige Aspekte der Benetzungstheorie und ihre Anwendung auf die Untersuchung und Veränderung der Oberflächeneigenschaften von Polymeren. Farbe und Lack 77 (1971) 997–1005 |
| [14] | Wu, S.: Polar and Nonpolar Interactions in Adhesion. The Journal of Adhesion 5 (1973) 39–55 |
| [15] | Marquis de Laplace, P. S.: Traité de Mécanique Céleste. Courcier, Paris (1805), Vol. 4, Supplément au Dixième Livre du Traité de Mécanique Céleste, 1–79 |
| [16] | Erhard, G.: Konstruieren mit Kunststoffen. 4. Auflage, Carl Hanser Verlag, München (2008), 152–153 (ISBN 978-3-446-41646-8; siehe: AMK-Büchersammlung unter G 33) |