Querkontraktion: Unterschied zwischen den Versionen

Version vom 3. März 2014, 10:56 Uhr

Querkontraktion

Unter der Voraussetzung eines schlanken runden Prüfkörpers, der sich im ebenen Spannungszustand (ESZ) befindet, tritt bei einer Zugbeanspruchung neben der Verlängerung $\Delta$ l des Prüfkörpers eine messbare Querschnittsverringerung $\Delta$ d infolge der Volumenkonstanz bei kleinen Deformationen auf. Diese Verringerung des Querschnitts wird auch als Querkontraktion bezeichnet und ergibt sich messtechnisch wie folgt [1]:

Verlängerung	:	$\Delta l=l-l_{0}\!$
Querkontraktion	:	$\Delta d=d_{0}-d\!$

Bei prismatischen Prüfkörpern wird gleichzeitig eine Verringerung der Dicke und der Breite des Prüfkörpers beobachtet:

Breitenänderung	:	$\Delta b=b_{0}-b\!$
Dickenänderung	:	$\Delta h=h_{0}-h\!$

Aus der relativen Veränderung der Prüfkörperdimension können die Dehnungen in der Längs- und Querrichtung berechnet werden, wobei voraussetzungsgemäß die relative Breiten- und Dickenänderung identisch sein soll:

Längsdehnung : $\varepsilon _{l}\,=\,{\frac {\Delta l}{l_{0}}}\!$

Querdehnung : $\varepsilon _{q}\,=\,{\frac {\Delta b}{b_{0}}}\!$

Der Quotient aus der Quer- und Längsdehnung wird als Querkontraktions- oder Poissonzahl bezeichnet und ist eine materialspezifische elastische Kenngröße, die bei dem Wert von 0,5 inkompressibles Werkstoffverhalten widerspiegelt:

Poissonzahl : $\mu \,=\,{\frac {\varepsilon _{q}}{\varepsilon _{l}}}\!$

Die Querkontraktionszahl ist bei Kunststoffen von der Temperatur und der Beanspruchungsgeschwindigkeit abhängig und liegt erfahrungsgemäß im Bereich von 0,3 bis 0,45. Für die Messung der Poissonzahl sind Präzisionsextensometer mit einer Auflösung von 0,1 µm erforderlich. Die Poissonzahl wird im Zugversuch bei einer Dehnrate von 1 mm/min im linearen Bereich des Dehnungsintervalls von 0,3 % < ε < ε_y ermittelt.

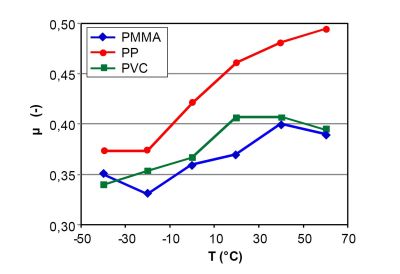
Eine umfassende Literaturanalyse zu den experimentellen Werten der Querkontraktions- oder Poissonzahlen ist in [2] für die Werkstoffe ABS, PA 6, PA 66, PA 6/GF, PA 66/GF, PAI, PBT, PC, PE-HD, PE-LD, PEEK, PEEK/GF, PEI, PEKK, PES, PI, PI/GF, PK, PMMA, POM, PP, PPA, PPA/GF, PPS, PPS/GF, PPSU, PS, PS/PPE, PTFE, PUR, PVC, PVC/GF, SAN und SB enthalten. Die Zusammenstellung wurde durch bisher nicht publizierte Messergebnisse ergänzt. Darüber hinaus sind Beispiele für die Abhängigkeit der Poissonzahl von der Temperatur und der normativen Dehnung angegeben (Bild 1).

Bild 1:

Abhängigkeit der Poissonzahl von der Temperatur für verschieden Werkstoffe

Literaturhinweise

[1]	Grellmann, W. Seidler, S.(Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2011) 2. Auflage, S. 121 (ISBN 978-3-446-42722-8; siehe AMK-Büchersammlung unter A 12)
[2]	Bierögel, C., Grellmann, W.: Quasi-Static Tensile Test. In: Grellmann, W., Seidler, S. (Hrsg.): Mechanical and Thermomechanical Properties of Polymers. Landoldt Börnstein. Volume VIII/6A2, Springer Verlag, Berlin (2014) S.136–142

@@ Zeile 1: / Zeile 1: @@
 <span style="font-size:1.2em;font-weight:bold;">Querkontraktion</span>
-Unter der Voraussetzung eines schlanken runden [[Prüfkörper|Prüfkörpers]], der sich im ebenen Spannungszustand (ESZ) befindet, tritt bei einer Zugbeanspruchung neben der Verlängerung <math>\Delta</math>l des [[Prüfkörper|Prüfkörpers]] eine messbare Querschnittsverringerung <math>\Delta</math>d infolge der Volumenkonstanz bei kleinen [[Deformation|Deformationen]] auf. Diese Verringerung des Querschnitts wird auch als Querkontraktion bezeichnet und ergibt sich messtechnisch wie folgt:
+Unter der Voraussetzung eines schlanken runden [[Prüfkörper|Prüfkörpers]], der sich im ebenen Spannungszustand (ESZ) befindet, tritt bei einer Zugbeanspruchung neben der Verlängerung <math>\Delta</math>l des [[Prüfkörper|Prüfkörpers]] eine messbare Querschnittsverringerung <math>\Delta</math>d infolge der Volumenkonstanz bei kleinen [[Deformation|Deformationen]] auf. Diese Verringerung des Querschnitts wird auch als Querkontraktion bezeichnet und ergibt sich messtechnisch wie folgt [1]:
 {|
 |Verlängerung
@@ Zeile 33: / Zeile 33: @@
 Poissonzahl	:<math>\mu\,=\, \frac{\varepsilon_q}{\varepsilon_l} \!</math>
-Die Querkontraktionszahl ist bei Kunststoffen von der Temperatur und der Beanspruchungsgeschwindigkeit abhängig und liegt erfahrungsgemäß im Bereich von 0,3 bis 0,45. Für die Messung der Poissonzahl sind Präzisionsextensometer mit einer Auflösung von 0,1 µm erforderlich.
+Die Querkontraktionszahl ist bei Kunststoffen von der Temperatur und der Beanspruchungsgeschwindigkeit abhängig und liegt erfahrungsgemäß im Bereich von 0,3 bis 0,45. Für die Messung der Poissonzahl sind Präzisionsextensometer mit einer Auflösung von 0,1 µm erforderlich. Die Poissonzahl wird im Zugversuch bei einer Dehnrate von 1 mm/min im linearen Bereich des Dehnungsintervalls von 0,3 % < &epsilon; < &epsilon;<sub>y</sub> ermittelt.
+Eine umfassende Literaturanalyse zu den experimentellen Werten der Querkontraktions- oder Poissonzahlen ist in [2] für die Werkstoffe ABS, PA 6, PA 66, PA 6/GF, PA 66/GF, PAI, PBT, PC, PE-HD, PE-LD, PEEK, PEEK/GF, PEI, PEKK, PES, PI, PI/GF, PK, PMMA, POM, PP, PPA, PPA/GF, PPS, PPS/GF, PPSU, PS, PS/PPE, PTFE, PUR, PVC, PVC/GF, SAN und SB enthalten. Die Zusammenstellung wurde durch bisher nicht publizierte Messergebnisse ergänzt. Darüber hinaus sind Beispiele für die Abhängigkeit der Poissonzahl von der Temperatur und der normativen Dehnung angegeben ('''Bild 1''').
-'''Literaturhinweis'''
+[[Datei:Querkontraktion1.jpg]]
+{|
+|- valign="top"
+|width="50px"|'''Bild 1''':
+|width="600px" |Abhängigkeit der Poissonzahl von der Temperatur für verschieden Werkstoffe
+|}
-* Grellmann, W. Seidler, S.(Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2011) 2. Auflage, S. 121 (ISBN 978-3-446-42722-8) (siehe [http://www.hs-merseburg.de/amk/index.php?otion=com_joomlib&Itemid=85 AMK-Büchersammlung] unter A 12)
+'''Literaturhinweise'''
+{|
+|-valign="top"
+|[1]
+|Grellmann, W. Seidler, S.(Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2011) 2. Auflage, S. 121 (ISBN 978-3-446-42722-8; siehe [http://www.hs-merseburg.de/amk/index.php?otion=com_joomlib&Itemid=85 AMK-Büchersammlung] unter A 12)
+|-valign="top"
+|[2]
+|Bierögel, C., Grellmann, W.: Quasi-Static Tensile Test. In: Grellmann, W., Seidler, S. (Hrsg.): Mechanical and Thermomechanical Properties of Polymers. Landoldt Börnstein. Volume VIII/6A2, Springer Verlag, Berlin (2014) S.136–142
+|}

Querkontraktion: Unterschied zwischen den Versionen

Version vom 3. März 2014, 10:56 Uhr

Navigationsmenü

Suche