SENB-Prüfkörper: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 6: | Zeile 6: | ||
== Anforderungen an die Prüfkörpergeometrie == | == Anforderungen an die Prüfkörpergeometrie == | ||
Bei der experimentellen Ermittlung bruchmechanischer Kennwerte sind die folgenden grundsätzlichen Bedingungen einzuhalten: | Bei der experimentellen Ermittlung [[Bruchmechanische Prüfung|bruchmechanischer Kennwerte]] sind die folgenden grundsätzlichen Bedingungen einzuhalten: | ||
# Die Prüfkörperabmessungen müssen unter den jeweiligen Prüfbedingungen wesentlich größer als die Ausdehnung der plastischen Zone an der | # Die Prüfkörperabmessungen müssen unter den jeweiligen Prüfbedingungen wesentlich größer als die Ausdehnung der plastischen Zone an der [[Riss]]spitze sein. | ||
# Die Kraft, die Kerbaufweitung und die Kraft-Kraftangriffspunkt-Verschiebung müssen kontinuierlich erfassbar sein. | # Die Kraft, die [[Rissöffnung|Kerbaufweitung]] und die Kraft-Kraftangriffspunkt-Verschiebung müssen kontinuierlich erfassbar sein. | ||
# Für die Berechnung des Spannungsintensitätsfaktor K im Moment der instabilen Rissausbreitung muss die Belastung des Prüfkörpers und die kritische Risslänge exakt bestimmbar sein. | # Für die Berechnung des [[Bruchmechanik#Linear-elastische_Bruchmechanik|Spannungsintensitätsfaktor K]] im Moment der [[Instabiler Riss|instabilen Rissausbreitung]] muss die Belastung des Prüfkörpers und die kritische Risslänge exakt bestimmbar sein. | ||
# Für die entsprechende Prüfkörpergeometrie muss die Bestimmungsgleichung, d.h. der Zusammenhang zwischen Beanspruchung und Risslänge bekannt sein. | # Für die entsprechende Prüfkörpergeometrie muss die Bestimmungsgleichung, d.h. der Zusammenhang zwischen Beanspruchung und Risslänge bekannt sein. | ||
Zur Erfüllung dieser Forderungen wurden eine Reihe von Festlegungen getroffen, die ausgehend von dem ASTM-Standard E 399 [1] in die bisher vorliegenden Standards Eingang gefunden haben. | Zur Erfüllung dieser Forderungen wurden eine Reihe von Festlegungen getroffen, die ausgehend von dem ASTM-Standard E 399 [1] in die bisher vorliegenden Standards Eingang gefunden haben. | ||
| Zeile 148: | Zeile 148: | ||
|-valign="top" | |-valign="top" | ||
|[3] | |[3] | ||
|Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München ( | |Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 251–254, (ISBN 978-3-446-44350-1; siehe [[AMK-Büchersammlung]] unter A 18) | ||
|-valign="top" | |-valign="top" | ||
|[4] | |[4] | ||
|[ | |[[MPK-Prozedur MPK-IKBV]] (2014-08): Prüfung von Kunststoffen – Instrumentierter Kerbschlagbiegeversuch: Prozedur zur Ermittlung des Risswiderstandverhaltens aus dem instrumentierten Kerbschlagbiegeversuch | ||
|-valign="top" | |-valign="top" | ||
|[5] | |[5] | ||
| Zeile 157: | Zeile 157: | ||
|-valign="top" | |-valign="top" | ||
|[6] | |[6] | ||
|Srawley, J.E., Gross, B.: Stress | |Srawley, J.E., Gross, B.: Stress Intensity Factors for Bend and Compact Specimens. Engineering Fracture Mechanics (1972) 587–589 | ||
|} | |} | ||
[[Kategorie:Biegeversuch]] | |||
[[Kategorie:Bruchmechanik]] | |||
[[Kategorie:Instrumentierter Kerbschlagbiegeversuch]] | |||
[[Kategorie:Prüfkörper]] | |||
Version vom 23. April 2015, 12:54 Uhr
SENB-Prüfkörper
Die angelsächsische Abkürzung SENB steht für "single-edge-notched bend" und der SENB-Prüfkörper wird im Deutschen als Dreipunktbiegeprüfkörper (3PB-Prüfkörper) bezeichnet.
Anforderungen an die Prüfkörpergeometrie
Bei der experimentellen Ermittlung bruchmechanischer Kennwerte sind die folgenden grundsätzlichen Bedingungen einzuhalten:
- Die Prüfkörperabmessungen müssen unter den jeweiligen Prüfbedingungen wesentlich größer als die Ausdehnung der plastischen Zone an der Rissspitze sein.
- Die Kraft, die Kerbaufweitung und die Kraft-Kraftangriffspunkt-Verschiebung müssen kontinuierlich erfassbar sein.
- Für die Berechnung des Spannungsintensitätsfaktor K im Moment der instabilen Rissausbreitung muss die Belastung des Prüfkörpers und die kritische Risslänge exakt bestimmbar sein.
- Für die entsprechende Prüfkörpergeometrie muss die Bestimmungsgleichung, d.h. der Zusammenhang zwischen Beanspruchung und Risslänge bekannt sein.
Zur Erfüllung dieser Forderungen wurden eine Reihe von Festlegungen getroffen, die ausgehend von dem ASTM-Standard E 399 [1] in die bisher vorliegenden Standards Eingang gefunden haben.
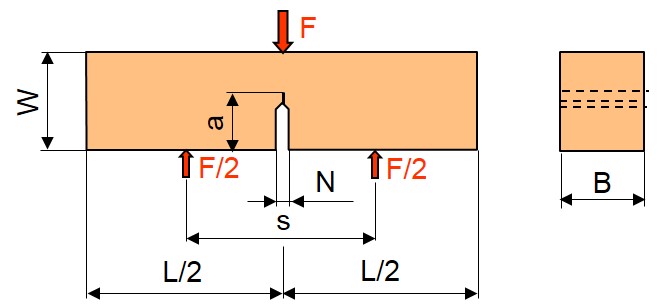
Prüfkörperform
|
|
| Bild: | Schematische Darstellung des SENB-Prüfkörpers |
Abmessungen (nach [1, 2]):
W = 2 B, Sonderform: W = B bis 4 B
s = 4 W Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \rightarrow}
s/W = 4, s = 40 mm
L = 4,5 W
a = (0,45–0,55) W
N Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ge}
1,5 mm bei U- und V-Kerb für Metalle
Typische Abmessungen für Kunststoffe (nach [3, 4]):
W = 10 mm
B = 4 mm (in Variation B = 2...10 mm)
L = 80 mm
s = 40 mm (in Variation s = 40...70 mm)
a = 2 mm (in Variation a = 0,5...7,5 mm)
N Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ge}
1,5 mm
l Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ge}
1,3 mm (Rasierklinge, Kerblänge)
r Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle < \!\ }
0,25 mm (Kerbradius)
r Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \approx}
0,125 µm (Rasierklinge, Kerbradius)
Bestimmungsgleichung
| Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K_I = \frac{F \cdot s}{B \cdot W^{3/2}} f(a/W)} |
| Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(a/W) \!\ } für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s/W = 4 \!\ } |
Tada [5]:
| Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_1(a/W) = 2,9(a/W)^{1/2}-4,6(a/W)^{3/2}+21,8(a/W)^{5/2}-37,6(a/W)^{7/2}+38,7(a/W)^{9/2} \!\ } |
Srawley und Gross [6]:
| Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_2(a/W) = \frac32(a/W)^{1/2} \cdot \frac{[1,99-a/W \cdot(1-a/W) \cdot (2,15-3,93a/W+2,7(a/W)^2)]}{(1+2a/W) \cdot (1-a/W)^{3/2}} \!\ } |
für s/W = 4
f2(a/W) zeigt Übereinstimmung mit f1 im Bereich 0<a/W<0,6, dann niedrigere Werte
Geometriekriterium für Metalle:
| Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle B, a, (W-a) \geq 2,5 \bigg(\frac {K_I}{R_e}\bigg)^2} |
Geometriekriterium für Kunststoffe:
| Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle B, a, (W-a) \geq \beta \bigg(\frac {K}{\sigma_y}\bigg)^2} |
es gilt: Re = Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma}
y = Streckspannung (Streckgrenze)
Die Geometriekonstante Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta}
ist werkstoffabhängig. (siehe auch Geometriekriterium, Bruchzähigkeit)
Literaturhinweise
| [1] | ASTM E 399 (2009): Standard Test Method for Linear-Elastic Plane-Strain Fracture Toughness KIc of Metallic Materials |
| [2] | Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig Stuttgart (1993) 3. Auflage, (ISBN 3-342-00659-5; siehe AMK-Büchersammlung unter E 29-3) |
| [3] | Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 251–254, (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18) |
| [4] | MPK-Prozedur MPK-IKBV (2014-08): Prüfung von Kunststoffen – Instrumentierter Kerbschlagbiegeversuch: Prozedur zur Ermittlung des Risswiderstandverhaltens aus dem instrumentierten Kerbschlagbiegeversuch |
| [5] | Tada, H., Paris, P.C., Irwin, G.R.: The Stress Analysis of Cracks Handbook, 3th Ed., ASME Press, New York (2000) |
| [6] | Srawley, J.E., Gross, B.: Stress Intensity Factors for Bend and Compact Specimens. Engineering Fracture Mechanics (1972) 587–589 |
