Geometriefunktion

Ein Service der
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung
PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Geometriefunktion

Die Geometriefunktion f (a/W)

Die endliche Geometrie eines jeden Bauteils und Prüfkörpers sowie die Rissgeometrie werden in der bruchmechanischen Werkstoffprüfung durch die Einführung einer Geometriefunktion f(a/W) berücksichtigt, womit der von Irwin eingeführte Spannungsintensitätsfaktor K in der Form

$K=\sigma _{N}\cdot \left(\pi a\right)^{\frac {1}{2}}\cdot f\left(a/W\right)$

geschrieben werden kann. Die Funktionen f (a/W) sind für eine Viezahl bruchmechanischer Prüfkörper berechnet worden. Das Bild enthält die Abmessungen von bevorzugt für Kunststoffe angewandten Prüfkörpern. Für einen unendlichen ausgedehnten Prüfkörper und den Grenzfall eines Risses mit einem Kerbradius $\rho$ ~ 0 ist f (a/W) = 1

Der Spannungsintensitätsfaktor erreicht zu Beginn der instabilen Rissausbreitung einen kritischen Wert K_Ic, der als Bruch- oder Risszähigkeit bezeichnet wird und die Dimension MPa mm^1/2 erhält. Die drei am meisten genutzten Prüfkörper sind der SENB-Prüfkörper, der SENT-Prüfkörper und der CT-Prüfkörper.

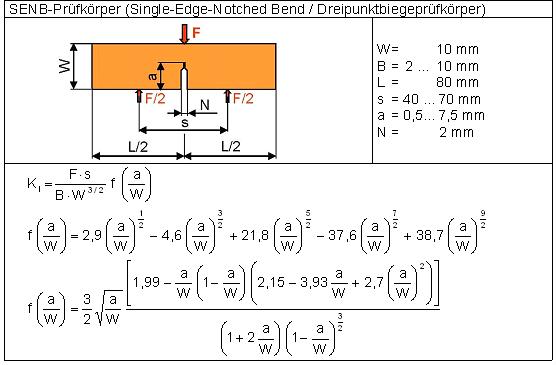
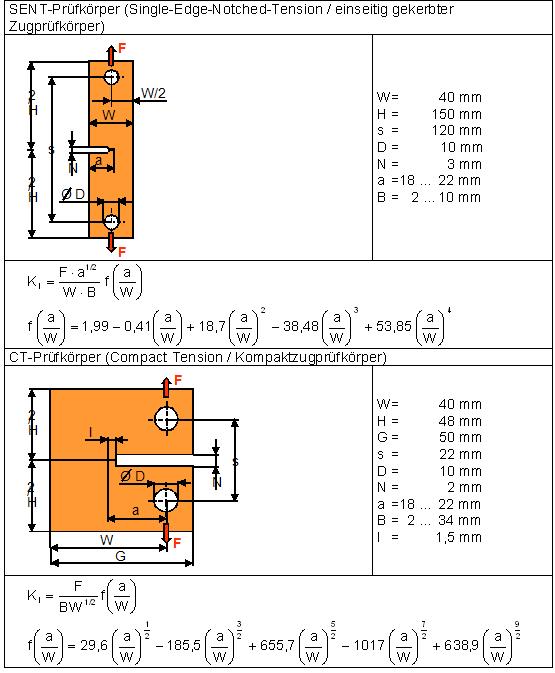
Ausgewählte Prüfkörperformen

Die Geometriefunktionen f (a/W) sind für eine Vielzahl von bruchmechanischen Prüfkörpern berechnet worden. Tabelle 1 erhält die Abmessungen von bevorzugt für Kunststoffe in der Prüfpraxis verwendete Prüfkörperformen.

Tabelle 1: Zusammenstellung häufig verwendeter Prüfkörperformen mit ihren Abmessungen, den dazugehörigen Bestimmungsgleichungen zur Berechnung der Bruchzähigkeiten und den Geometriefunktionen

Literaturhinweise

• Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 251/252 (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18)
• Anderson, T. L.: Fracture Mechanics. Fundamentals and Applications. 3rd Ed, CRC Press Boca, Raton (2005) (ISBN 978-0849342608; siehe AMK-Büchersammlung unter E 8-2)
• Irwin, G. R.: Analysis of Stress and Strains Near the End of a Crack Traversing a Plate. J. Appl. Mech. 24 (1957) 361
• Tada, H., Paris, P. C., Irwin, G. R.: The Stress Analysis of Cracks Handbook. 3^th Ed., ASME Press, New York (2000)