Auswertemethode nach Kanazawa: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 121: | Zeile 121: | ||
Im Ergebnis von umfangreichen Untersuchungen zur Risslängenabhängigkeit des J-Integrals wurde in [1, 5] nachgewiesen, dass die J-Auswertemethoden von Kanazawa und [[Auswertemethode_nach_Rice,_Paris_und_Merkle|Rice, Paris und Merkle]] für kleine Risslängen zu hohe bruchmechanische Kennwerte liefern. | Im Ergebnis von umfangreichen Untersuchungen zur Risslängenabhängigkeit des J-Integrals wurde in [1, 5] nachgewiesen, dass die J-Auswertemethoden von Kanazawa und [[Auswertemethode_nach_Rice,_Paris_und_Merkle|Rice, Paris und Merkle]] für kleine Risslängen zu hohe bruchmechanische Kennwerte liefern. | ||
==Siehe auch== | |||
*[[J-Integral Auswertemethoden|J-Integral Auswertemethoden (Überblick)]] | |||
*[[J-Integral-Konzept]] | |||
Version vom 30. September 2024, 12:27 Uhr
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Auswertemethode nach Kanazawa
J-Integral-Auswertungsmethode
Grundannahme der Auswertemethode
Bei der Bestimmung von bruchmechanischen Kennwerten nach dem J-Integral-Konzept werden J-Integral-Auswertemethoden eingesetzt [1].
Bei der J-Integral-Auswertemethode nach Kanazawa [2–4] wird zur Bestimmung von -Werten eine komplementäre Verformungsenergie AK eingeführt. Er modifizierte den Berechnungsansatz nach Rice, da bei Rice für geringe Risslängen zu kleine J-Werte erhalten wurden. Kanazawa leitete hierfür eine Korrekturfunktion ab.
| mit |
Damit ergibt sich der J-Wert allgemein zu:
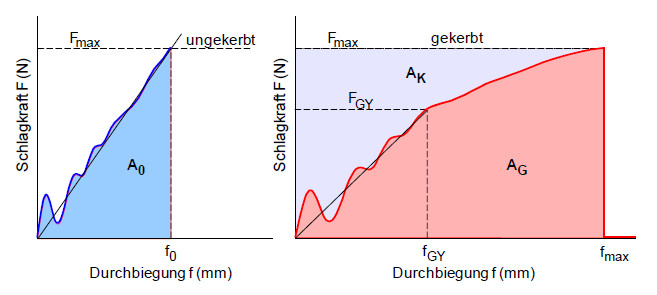
| Bild 1: | Bestimmung des J-Integrals nach der Auswertemethode von Kanazawa |
Bestimmungsgleichung für Single-Edge-Notched Bend (SENB)-Prüfkörper
Für den konkreten Fall des SENB-Prüfkörpers gilt für die Bestimmungsgleichung:
mit: AK = Fmax fmax − AG als komplementäre Verformungsenergie
für 0 < a/W < 1 und
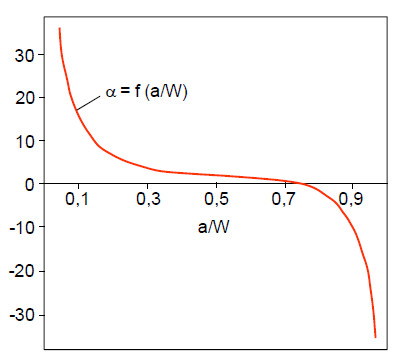
Die Bedeutung von α für die bruchmechanische Kennwertermittlung mit Hilfe von Dreipunktbiegeprüfkörpern kann unter Verwendung der entsprechenden Geometriefunktion f(a/W) von Tada [6]
aus der grafischen Darstellung in Bild 2 abgeleitet werden.
| Bild 2: | Geometriefunktion des J-Integralauswerteverfahrens nach Kanazawa in Abhängigkeit vom a/W-Verhältnis für Dreipunktbiegebeanspruchung und s/W = 4 |
Bestimmungsgleichung für Compact Tension (CT)-Prüfkörper
Für den CT-Prüfkörper gelten folgende Bestimmungsgleichungen:
| mit |
Im Ergebnis von umfangreichen Untersuchungen zur Risslängenabhängigkeit des J-Integrals wurde in [1, 5] nachgewiesen, dass die J-Auswertemethoden von Kanazawa und Rice, Paris und Merkle für kleine Risslängen zu hohe bruchmechanische Kennwerte liefern.
Siehe auch
Literaturhinweise
| [1] | Grellmann, W.: Beurteilung der Zähigkeitseigenschaften von Polymerwerkstoffen durch bruchmechanische Kennwerte. Habilitation (1986), Technische Hochschule Merseburg, Wiss. Zeitschrift TH Merseburg 28 (1986), H 6, S. 787–788 (Inhaltsverzeichnis, Kurzfassung) |
| [2] | Schwalbe, K.-H.: Bruchmechanik metallischer Werkstoffe. Carl Hanser Verlag, München Wien (1980), (ISBN 3-446-12983-9; siehe AMK-Büchersammlung unter E 15) |
| [3] | Kanazawa, T., Machida, D., Onozuka, M., Kaned, S.: Report of the University of Tokyo HWx-779-75 in [4] |
| [4] | Kromp, K., Pabst, R. F.: Über die Ermittlung von J-Integralwerten bei keramischen Werkstoffen im Hochtemperaturbereich. Materialprüfung 22 (1980) 6, S. 241–245 |
| [5] | Grellmann, W., Sommer, J.-P.: Beschreibung der Zähigkeitseigenschaften von Polymerwerkstoffen mit dem J-Integralkonzept. Institut für Mechanik, Berlin und Karl-Marx-Stadt, Fracture Mechanics, Micromechanics and Coupled Fields – (FMC)-Series (1985) 17, S. 48–72 |
| [6] | Tada, H., Paris, P. C., Irwin, G. R.: The Stress Analysis of Cracks Handbook. Hellertown Pennsylvania, Del. Res. Corp. (1973) |





![{\displaystyle J_{Id}^{K}={\frac {1}{B}}\left[({\frac {2}{W-a}}-{\frac {\alpha }{W}})A_{G}+{\frac {\alpha }{W}}(F_{max}f_{max})-({\frac {2}{W-a}}+{\frac {\alpha }{W}})A_{0}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62ef2a8b049b1be72782a83fc851f842eeba2d80)


![{\displaystyle J_{Ic}^{K}={\frac {1}{B}}\left[{\frac {1}{(W-a)}}A_{G}+({\frac {\alpha }{W}}-{\frac {1}{(W-a)}})A_{K}-{\frac {\alpha }{W}}A_{0}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/095130c951c3378f416d23a893232f92aa4cf1a0)
![{\displaystyle J_{Ic}^{K}={\frac {1}{B}}\left[{\frac {1}{(W-a)}}A_{G}+({\frac {\alpha }{W}}-{\frac {1}{(W-a)}})(F_{max}f_{max}-A_{G})-{\frac {\alpha }{W}}A_{0}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cceae92e6b9c5014393dfde0551fe517962ca2ab)
![{\displaystyle J_{Ic}^{K}={\frac {1}{B}}\left[{\frac {A_{G}}{(W-a)}}{\frac {\alpha }{W}}F_{max}f_{max}-{\frac {\alpha }{W}}A_{G}-{\frac {F_{max}f_{max}}{(W-a)}}+{\frac {A_{G}}{(W-a)}}-{\frac {\alpha }{W}}A_{0}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0325de8753c8baad57f5f6c1cf042ba6da5ee200)
![{\displaystyle J_{Ic}^{K}={\frac {1}{B}}\left[{\frac {2A_{G}-F_{max}f_{max}}{(W-a)}}+{\frac {\alpha }{W}}(F_{max}f_{max}-A_{G}-A_{0})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/834badaf92de58a8bd1aa6d0098b67c5e7606af3)
![{\displaystyle J_{Ic}^{K}={\frac {1}{B}}\left[{\frac {1}{(W-a)}}(2A_{G}-F_{max}f_{max})+{\frac {\alpha }{W}}(F_{max}f_{max}-A_{G}-A_{0})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c73095db91723dabc796cfcfa2936bf51d9016fe)
