Arcan-Prüfkörper: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 35: | Zeile 35: | ||
<math>\sigma_{\infty}=\sigma_A \cdot sin \alpha</math> | <math>\sigma_{\infty}=\sigma_A \cdot sin \alpha</math> | ||
<math>\tau_{\infty}=\sigma_A \cdot cos \alpha</math> | <math>\tau_{\infty}=\sigma_A \cdot cos \alpha</math> | ||
Basierend auf den Normal- und Scherspannungskomponenten können die Spannungsintensitätsfaktoren K<sub>I</sub> (Modus I) und K<sub>II</sub> (Modus II) bestimmt werden: | |||
<math>K_I=\sigma_{\infty} \cdot \sqrt{\pi \cdot a} \cdot f_I \left(a/c\right)</math> | |||
<math>K_II=\tau_{\infty} \cdot \sqrt{\pi \cdot a} \cdot f_{II} \left(a/c\right)</math> | |||
== Literaturhinweise === | == Literaturhinweise === | ||
Version vom 10. Januar 2011, 16:54 Uhr
Arcan-Prüfkörper
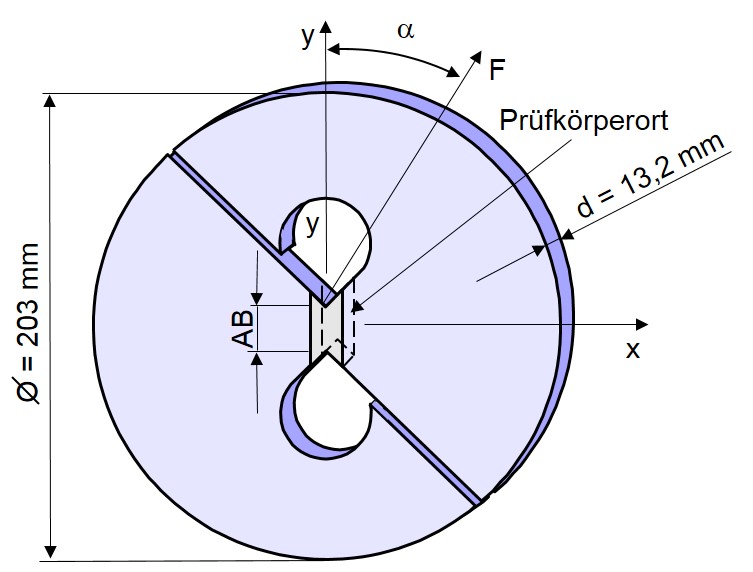
Der Arcan-Prüfkörper und die Arcan-Vorrichtung wurden nach ihrem Erfinder bezeichnet [1]. Sie wurde mit dem Ziel entwickelt, eine gleichförmige ebene Spannung in den Testbereich zu erhalten (siehe Bild 1).
Bild 1: Arcan-Testvorrichtung und Prüfkörpergeometrie
Der Prüfkörper wird mit einem einseitigen Anfangsriss versehen (z.B. V-Kerb). Erfolgt die Belastung in y-Richtung erhält man folgende Beanspruchungsmoden:
| Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha} =0° | Mode I |
| Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha} =45° | Mixed Mode |
| =90° | Mode I |
Durch Veränderung des Winkels Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha}
wird ein kombinierter Zug- und Scherspannungszustand im Testbereich erreicht. Ein Vorteil dieses Prüfkörpers ist die Wiederverwendbarkeit der Metallvorrichtung. Der Verbundwerkstoffprüfkörper wird an die Metallvorrichtung geklebt und kann nach dem Testen durch erhitzen des Prüfkörpers und der Vorrichtung über die Glasübergangstemperatur des Klebers abgelöst werden.
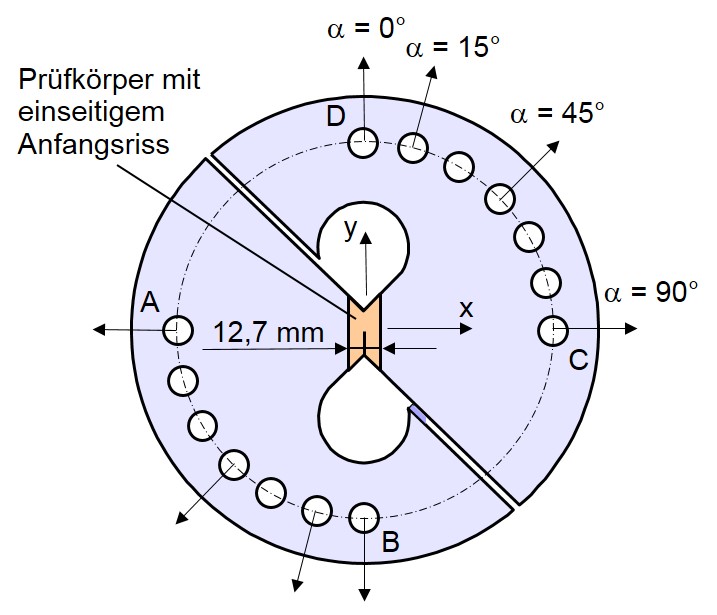
Jurf und Pipes [2] erweiterten den Nutzen der Vorrichtung durch den Austausch derr charakteristischen V-gekerbten Arcan-Prüfkörper mit einem einseitig angerissenen Prüfkörper (siehe Bild 2).
Bild 2: Arcan-Bruchmechanikprüfkörper
Durch Veränderung des Winkels (Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha)} von auf 90° können Werte für Modus II, Mixed-Mode und Modus I gesammelt werden. Der gewählte Belastungswinkel wird durch Montierung der Vorrichtung mit zwei gegenüberliegenden Bohrungen erreicht.
Bestimmungsgleichung für Spannungsintensitätsfaktoren
Für einen gegebene Winkel Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha} können die "Fernfeld"-Normal- und Scherspannung erhalten werden, wobei die Spannung Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_A} als die aufgewendete Kraft F dividiert durch die Querschnittsfläche (A) des Verbundwerkstoffprüfkörpers definiert ist.
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_{\infty}=\sigma_A \cdot sin \alpha}
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tau_{\infty}=\sigma_A \cdot cos \alpha}
Basierend auf den Normal- und Scherspannungskomponenten können die Spannungsintensitätsfaktoren KI (Modus I) und KII (Modus II) bestimmt werden:
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K_I=\sigma_{\infty} \cdot \sqrt{\pi \cdot a} \cdot f_I \left(a/c\right)}
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K_II=\tau_{\infty} \cdot \sqrt{\pi \cdot a} \cdot f_{II} \left(a/c\right)}