Brucharten

Brucharten

In der Bruchmechanik unterscheidet man bei der makroskopischen Betrachtung von Bruchflächen zunächst zwischen dem Normalspannungsbruch (Trennbruch) und dem Scherbruch.
Je nach der Art der mechanischen Beanspruchung spricht man bei einseitiger Beanspruchung von Gewaltbruch und bei wechselseitiger Beanspruchung von Schwingbruch.

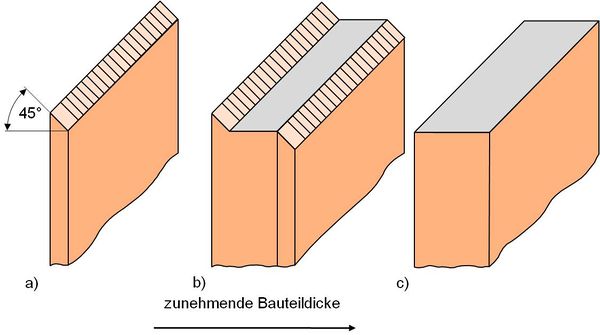
Als ein makroskopisches Merkmal kann entweder das Ausmaß der dem Bruch vorangegangenen plastischen Verformung oder die vom Spannungszustand und der Bauteildicke abhängige Bruchform (Bild 1) herangezogen werden [1].

Bild 1:

Makroskopische Bruchmerkmale an plattenförmigen Bauteilen (nach [1]) a) Scherbruch (scherflächiger Bruch) b) Trennbruch mit Scherlippen c) Normalspannungsbruch (Trennbruch; normalflächiger Bruch)

Der Scherbruch (oder auch Schubbruch) (Bild 1a) ist eine Folge des ebenen Spannungszustandes (ESZ), wie er in Bauteilen konstanter Dicke, die wesentlich kleiner ist als die übrigen Abmessungen, durch Belastung in der Bauteilebene näherungsweise auftritt. Das Versagen wird durch das Überschreiten kritischer Schubspannungen eingeleitet.
Im Gegensatz dazu kann sich in dickeren Bauteilen ein ebener Dehnungszustand (EDZ) ausbilden, der zum Trennbruch führt. Die Trennung tritt senkrecht (normal) zur Zugbeanspruchung ein. Die Form 1b entspricht einem gemischten Spannungszustand (ebener Spannungszustand am Rand, ebener Dehnungszustand bzw. dreiachsiger Spannungszustand im Inneren des Bauteils). Mit zunehmender Bauteildicke wächst die Neigung zum Normalspannungsbruch (normalflächigen Trennbruch) (Bild 1c), so dass die Breite der am Rand auftretenden Scherlippen ein Maß für die Plastizitätsreserve ist. Die Scherlippen entstehen als plastische Deformation im Bereich des ebenen Spannungszustandes als Folge der freien Verformbarkeit an der Oberfläche des Bauteils. Die Größe ist abhängig vom Werkstoff aber auch von den Umgebungsbedingungen, wie Beanspruchungstemperatur und -geschwindigkeit. Bei gleichbleibenden Beanspruchungs- und Umgebungsbedingungen nimmt mit zunehmender Wandstärke der Bereich auf der Bruchfläche zu, in dem der ebene Dehnungszustand zu einem verformungsarmen Trennbruch führt. Der Bereich, in dem sich infolge des ebenen Spannungszustands die Scherlippen bilden, bleibt dagegen konstant.

Die mikroskopischen Bruchmerkmale werden vom Bruchmechanismus, d.h. den Vorgängen bei der Rissausbreitung, bestimmt. Neben den beiden Grundmechanismen der Spaltung und Scherung kann bei kristallinen Werkstoffen auch die trans- bzw. interkristallin verlaufende Rissausbreitung als ein Bruchmerkmal angesehen werden. Bild 2 zeigt die Grundtypen mikroskopischer Bruchmerkmale von Kunststoffen [1].

Bild 2:

Ausgewählte mikroskopische Bruchmerkmale für Kunststoffe a) verformungsarmer Sprödbruch mit Crazebildung b) verformungsarmer Sprödbruch mit Rampen bzw. Schollen c) Verformungsbruch mit Hof um den Einschluss d) Verformungsbruch (große plastische Deformation mit Zipfelbildung) e) Bruch mit Wellen bzw. Rastlinien als Folge unterschiedlicher Rissausbreitungsgeschwindigkeit f) Bruch eines faserverstärkten Kunststoffes mit guter Faser-Matrix-Haftung

Ein für Kunststoffe sehr häufig betrachteter mikromechanischer Deformationsmechanismus ist das Crazing.
Crazes sind Normalspannungsanrisse, die unter Zugbeanspruchung stehend, parallel zur Belastungsrichtung plastisch verstrecktes Material enthalten. Die zugbelasteten Bereiche werden durch verstreckte Fibrillen entlastet. Ehrenstein [2] bezeichnet diese Deformationserscheinungen als „stabilisierte“ Gewaltanrisse, deren Trennflächen von verstreckten Fibrillen und Fasern überbrückt werden mit einem Fibrillendurchmesser von 0,01 bis 0,1 µm.
Crazes können sowohl an freien Oberflächen als auch im Innern des Prüfkörpers entstehen und sind dementsprechend halbkreis- bzw. kreisförmig begrenzt. Bei durchsichtigen Kunststoffen kann man die Ausdehnung des Kreises mit dem bloßen Auge erkennen (Weißbruch) [2].

Literaturhinweise

[1]	Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig Stuttgart (1982) (siehe AMK-Büchersammlung unter E 29–1)
[2]	Ehrenstein, G. W.; Engel, K.; Klingele, H.; Schaper, H.: SEM of Plastics Failure / REM von Kunststoffschäden. Carl Hanser Verlag, München Wien (2011), ISBN 978-3-446-42242-1 (siehe AMK-Büchersammlung unter D 5)