Dielektrischer Verlustfaktor: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 70: | Zeile 70: | ||
|-valign="top" | |-valign="top" | ||
|[2] | |[2] | ||
|Schönhals, A.: Elektrische und dielektrische Eigenschaften. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015), 3. Auflage, S. 357–398 (ISBN 978-3-446-44350-1; siehe [[AMK-Büchersammlung]] unter A 18) | |Schönhals, A.: Elektrische und dielektrische Eigenschaften. In: [https://www.researchgate.net/profile/Wolfgang-Grellmann Grellmann, W.], Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015), 3. Auflage, S. 357–398 (ISBN 978-3-446-44350-1; siehe [[AMK-Büchersammlung]] unter A 18) | ||
|-valign="top" | |-valign="top" | ||
|[3] | |[3] | ||
Version vom 23. März 2023, 11:38 Uhr
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Dielektrischer Verlust
Grundlagen
Durch ein elektrisches Feld wirken in einem Kunststoff (Dielektrikum) Kräfte, welche die molekulare Elektrostatik beeinflussen und die zu einer Ladungsverschiebung zwischen angrenzenden Potentialflächen führen. Damit ist eine Polarisation des Dielektrikums verbunden, die eine wesentliche Eigenschaft des Kunststoffes darstellt. Im Folgenden wird auf die prinzipielle Messanordnung der dielektrischen Spektroskopie [1, 2] und die Bestimmung des dielektrischen Verlustfaktors eingegangen.
Messaufbau
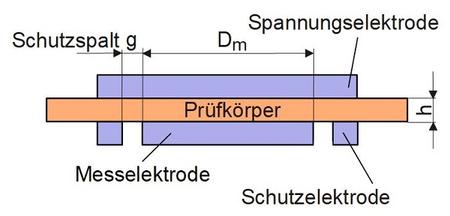
Als Messeinrichtung wird ein Plattenkondensator mit konzentrischer Elektrodenanordnung und variabler Spaltdicke verwendet. Sein prinzipieller Aufbau ist in der DIN 62631 [3] (Bild 1) dargestellt. Die ringförmige Schutzelektrode gewährleistet dabei ein homogenes elektrisches Feld im Bereich der Messelektrode [3–6].
| Bild 1: | Schematischer Aufbau des Messkondensators nach [3] |
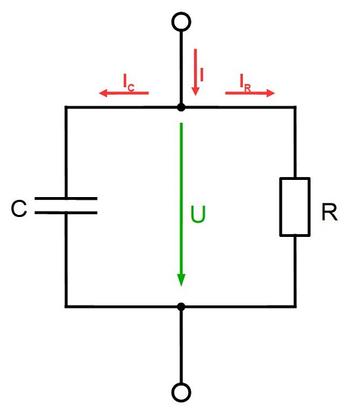
Beim Anlegen eines Wechselfeldes entsteht aufgrund der Phasenverschiebung zwischen dem ohmschen Widerstand und dem kapazitiven Widerstand ein Verlust an elektrischer Energie, der in Wärme umgesetzt wird. In einem idealen Kondensator wird dabei nur Blindleistung umgesetzt. Das ist die Leistung, die nicht nach außen in Erscheinung tritt, wodurch dem Stromkreis keine Energie entzogen wird. Reale Kondensatoren besitzen aufgrund des vorhandenen Dielektrikums auch eine Wirkleistung. Deshalb muss in der Berechnung des Verlustfaktors ein ohmscher Widerstand berücksichtigt werden.
| Bild 2: | Ersatzschaltbild eines realen Kondensators |
Das Bild 2 zeigt das Ersatzschaltbild als Parallelschaltung von Kondensator und ohmschen Widerstand. Mit Hilfe des KIRCHHOFF‘schen Knotensatzes und der Strom-Spannungsrelation wird der komplexe Widerstand dieser Schaltung nach Gl. (1) bestimmt.
| (1) |
Ermittlung des Kennwertes für den dielektrischen Verlust
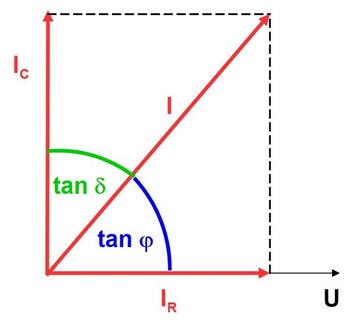
Anhand des Ersatzschaltbildes aus Bild 2 ergibt sich das Strom-Zeiger-Diagramm nach Bild 3. Entsprechend Gl. (2) kann dann der Phasenwinkel φ angeben werden.
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle \tan \varphi ={\frac {Im(I)}{Re(I)}}=\omega \cdot R\cdot C} | (2) |
Wegen der in der Praxis geringen Abweichung des Stromvektors I von der imaginären Achse (IC) wird als Verlustfaktor oder -winkel der Winkel δ zwischen dieser Achse und der resultierenden entsprechend Gl. (3) verwendet [5].
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle \tan \delta ={\frac {1}{\omega \cdot R\cdot C}}} | (3) |
| Bild 3: | Strom-Zeiger-Diagramm für das Ersatzschaltbild des realen Kondensators |
Mit Hilfe der Gleichung (3) ist der Verlustfaktor tan δ einfach bestimmbar, wenn der ohmsche Widerstand gemessen werden kann. Dieser beschreibt jenen Energieverlust des Dielektrikums, der bei Anlegen einer Wechselspannung bei der Umkehrung der Polarisation entsteht. Damit ist der dielektrische Verlust in Form des Verlustfaktors eine Messgröße, die Eigenschaftsänderungen mit hoher Empfindlichkeit darstellen kann.
Literaturhinweise
| [1] | Busse, G.: Dielektrische Spektroskopie. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015), 3. Auflage, S. 484–485 (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18) |
| [2] | Schönhals, A.: Elektrische und dielektrische Eigenschaften. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015), 3. Auflage, S. 357–398 (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18) |
| [3] | DIN EN IEC 62631-2-1 (2018-12): Dielektrische und resistive Eigenschaften fester Elektroisolierstoffe – Teil 2-1: Relative Permittivität und Verlustfaktor – Technische Frequenzen (0,1 Hz – 10 MHz) – Wechselspannungsverfahren |
| [4] | DIN IEC 60093 (1993-12): Prüfverfahren für Elektroisolierstoffe – Spezifischer Durchgangswiderstand und spezifischer Oberflächenwiderstand von festen, elektrisch isolierenden Werkstoffen. VDE 0303-30:1993-12 (zurückgezogen; ersetzt durch DIN EN 62631-3-1 (2017-01); DIN EN 62631-3-2 (2016-10)) |
| [5] | DIN EN 62631-3-1 (2017-01): Dielektrische und resistive Eigenschaften fester Isolierstoffe – Teil 3-1: Bestimmung resistiver Eigenschaften (Gleichspannungsverfahren) – Durchgangswiderstand und spezifischer Durchgangswiderstand – Basisverfahren |
| [6] | DIN EN 62631-3-2 (2016-10): Dielektrische und resistive Eigenschaften fester Isolierstoffe – Teil 3-2: Bestimmung resistiver Eigenschaften (Gleichspannungsverfahren) – Oberflächenwiderstand und spezifischer Oberflächenwiderstand |
| [7] | Lindner, H., Siebke, W., Simon, G., Wuttke, W.: Physik für Ingenieure. Fachbuchverlag Leipzig im Carl Hanser Verlag (2006), 17. Auflage, (ISBN 978-3-446-40609-4) (siehe AMK-Büchersammlung unter I 56) |