DENT-Prüfkörper

Ein Service der
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung
PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

DENT-Prüfkörper

Alllgemeines

Die angelsächsische Abkürzung DENT steht für "Double-Edge-Notched Tension" und der DENT-Prüfkörper wird im Deutschen als doppelseitig gekerbter Zugprüfkörper (oder auch beidseitig gekerbter Zugprüfkörper) bezeichnet.

Prüfkörperform

Bild 1:

Schematische Darstellung des DENT-Prüfkörpers

Abmessungen (nach [1]):
${\frac {H}{W}}\geq 3$

Typische Abmessungen für Kunststoffe [2]:
H = 75 $\pm$ 1 mm
W = 10 $\pm$ 0,5 mm
B = 3 bzw. 4 mm
a = 1 $\pm$ 0,2 mm

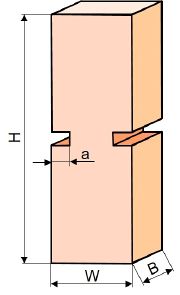
Bestimmungsgleichung für den Spannungsintensitätsfaktor [3]

$K_{I}={\frac {F_{max}}{B\cdot W}}\cdot f_{1}(a/W)$

$K_{I}={\frac {F_{max}}{B\cdot W}}\cdot f_{2}(a/W)$

$f_{1}(a/W)={\sqrt {\pi a}}\cdot {\frac {1}{1-{\frac {2a}{W}}}}\cdot {\sqrt {\frac {1,26+2,18{\frac {a}{W\left({\frac {1}{2}}-a\right)}}}{1+3,63{\frac {a}{W\left({\frac {1}{2}}-a\right)}}+5,31\left[{\frac {a}{W\left({\frac {1}{2}}-a\right)}}\right]^{2}}}}\!\$

$f_{2}(a/W)={\sqrt {\pi a}}\cdot {\sqrt {{\frac {W}{\pi a}}\left(tan{\frac {\pi a}{W}}+0,1sin{\frac {\pi a}{W\cdot {\frac {1}{2}}}}\right)}}$

Anwendung

Die Anwendung des DENT-Prüfkörpers erfolgt im quasistatischen Zugversuch vorwiegend für Kunststoffe mit hoher Matrixzähigkeit, aber in den letzten Jahren auch in der Elastomer- und Folienprüfung [2, 4]. Auf Grund von Problemen bei der Einspannung wird in den DENT-Prüfkörpern eine zusätzliche Bohrung zur verbesserten Halterung eingebracht.

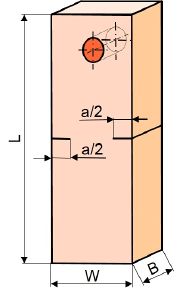
Bild 2:

Schematische Darstellung eines DENT-Prüfkörpers für bruchmechanische Experimente an elastomeren Werkstoffen mit dem instrumentierten Kerbschlagzugversuch

Auswertung

Für die Auswertung von instrumentierten Kerbschlagzugversuchen an Elastomerwerkstoffen, d. h. für die Berechnung von J_d-Werten als Widerstand gegen instabile Risseinleitung und -ausbreitung werden die folgenden Gleichungen (1) und (2) verwendet.

$J_{d}={\frac {\eta \cdot A_{max}}{B\cdot \left(W-a\right)}}$

mit

Amax		Verformungsenergie und
$\eta$		nach [5] in der Form

$\eta =-0,06+5,99(a/W)-7,42(a/W)^{2}+3,29(a/W)^{3}\!\$

Eine umfangreiche Zusammenstellung von geeigneten Prüfkörpern für bruchmechanische Untersuchungen an Kunststoffen und Verbundwerkstoffen ist in Bruchmechanikprüfkörper enthalten.

Siehe auch

• Essential Work of Fracture (EWF)-Konzept
• Instrumentierter Kerbschlagzugversuch
• Folienprüfung

Literaturhinweise

[1]	Sähn, S., Göldner, H.: Bruch- und Beurteilungskriterien in der Festigkeitslehre. Fachbuchverlag, Leipzig Köln (1993) S. 36, (ISBN 3-343-00854-0; siehe AMK-Büchersammlung unter E 26)
[2]	Reincke, K., Grellmann, W.: Instrumentierte Schlagzugprüfung von Elastomeren. In: Frenz, H. und Wehrstedt, A. (Hrsg.): Kennwertermittlung für die Praxis – Tagungsband Werkstoffprüfung 2002. Wiley-VCH, Weinheim (2003) S. 340–344, (ISBN 3-527-30674-9; siehe AMK-Büchersammlung unter M 10)
[3]	Richard, H.-A.: Interpolationsformel für Spannungsintensitätsfaktoren VDI-Zeitschrift 121 (1979) 22 - Nov. II 1138–1143
[4]	Reincke, K.: Bruchmechanische Bewertung von ungefüllten und gefüllten Elastomerwerkstoffen. Mensch und Buch Verlag (2005), (ISBN 978-3-86664-021-4; siehe AMK-Büchersammlung unter B 1-13)
[5]	Anderson, T. L.: Fracture Mechanics. Fundamentals and Applications, 3rd Ed., CRC Press Boca Raton (2005), (ISBN 978-08493-4260-8; siehe AMK-Büchersammlung unter E 8), DOI: https://doi.org/10.11201/9781420058215