Peelverhalten – Modellierung

Ein Service der
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung
PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Peelverhalten – Modellierung

Finite-Elemente-Methode (FEM)

Eine Möglichkeit den Peelvorgang auf numerischem Weg nachzuvollziehen, besteht in der Erstellung eines Simulationsmodells auf Basis der Finite-Elemente-Methode (FEM). Ein solches Modell ermöglicht beispielsweise den Zugang zu experimentell schwierig ermittelbaren Werkstoffkenngrößen und trägt zur Begrenzung des experimentellen Aufwands bei [1].
Das Ablösen zweier Schichten kann unter Verwendung kohäsiver Elemente mit Hilfe der Finite-Elemente-Methode simuliert werden [2–5].

Modellierung des Peelverhaltens von PE-LD/iPB-1

Am Beispiel des Peelfolienblendsystems Polyethylen niederer Dichte und isotaktisches Polybuten-1 (Kurzzeichen: PE-LD/iPB-1) soll nachfolgend die Modellierung des Peelverhaltens unter Verwendung der FEM beschrieben werden. Es kam ein zweidimensionales Modell mit 6500 Elementen und ca. 14500 Verschiebungsfreiheitsgraden zur Anwendung [6]. Eine effiziente Nutzung der Elementanzahl führte zu einer groben Diskretisierung im Bereich der Peelarme mit den Elementabmaßen Höhe/Länge = 1/5 und einer feinen Diskretisierung im Bereich der Siegelnaht mit den Elementabmaßen Höhe/Länge = 1/1 (Bild 1) bei einer gegebenen Länge der Siegelnaht von 15 mm.

Bild 1:

Finite-Elemente-Modell des Peelprüfkörpers

Zur numerischen Simulation des Peelvorgangs benötigt das Finite-Elemente-Modell (FE-Modell), neben den charakteristischen Eigenschaften des Folienmaterials, verschiedene experimentelle Daten als Input, insbesondere eine Kohäsivspannungs-Relativverschiebungs-Beziehung als Grundlage der numerischen Berechnung mit Hilfe von Kohäsiv-Zonen-Elementen. Auf Basis der experimentellen Ergebnisse wird vereinfacht von linear-elastischem Werkstoffverhalten (siehe: HOOKE´sche Gesetz) für die Abbildung des Folienmaterials im FE-Modell ausgegangen. Nachfolgend werden die Schritte zur Ermittlung der Kohäsivspannungs-Relativverschiebungs-Beziehung für das PE-LD/iPB-1-Peelfolienblendsystem mit unterschiedlichen iPB-1-Masseanteilen erläutert.
Im ersten Schritt wurde die Kohäsivenergie $\Gamma$_c, die der Fläche unter der Kohäsivspannungs-Relativverschiebungs-Kurve entspricht, nach Gl. (1) berechnet.

$\Gamma _{c}\,=\,{\frac {E_{G}}{2A}}$

(1)

mit

EG		Gesamtpeelenergie
A		Siegelnahtfläche

In einem weiteren Schritt wurde die maximale Kohäsivspannung T_max nach Gl. (2) berechnet.

$T_{max}\,=\,{\frac {F_{peel}}{B}}$

(2)

mit

Fpeel		Peelkraft
B		Querschnitt der Folie

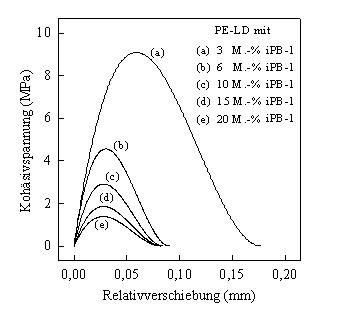
Anschließend wurde unter Verwendung der Kohäsivenergie $\Gamma$_c und der maximalen Kohäsivspannung T_max die Kohäsivspannungs-Relativverschiebungs-Beziehung mit Hilfe eines Polynoms dritten Grades erstellt. In Bild 2 sind die Kohäsivspannungs-Relativverschiebungs-Beziehungen für PE-LD mit unterschiedlichen iPB-1-Masseanteilen dargestellt. Sowohl die Kohäsivenergie $\Gamma$_c als auch die maximale Kohäsivspannung T_max und die maximale Relativverschiebung $\delta$_e werden mit zunehmendem iPB-1-Masseanteil vermindert. Den größten Einfluss auf die Form der Kurve und somit auf den simulierten Peelvorgang hat dabei die Kohäsivenergie $\Gamma$_c [6]. Die ermittelten Kohäsivspannungs-Relativverschiebungs-Beziehungen können nun vom FE-Modell zur Simulation des Peelvorgangs der einzelnen kohäsiven Elemente verwendet werden. Zusätzlich müssen verschiedene Werkstoffkenngrößen wie Elastizitätsmodul und Querkontraktionszahl des verwendeten Prüfkörpermaterials im FE-Modell ergänzt werden.

Bild 2:

Kohäsivspannungs-Relativverschiebungs-Kurven von PE-LD mit verschiedenen iPB-1-Masseanteilen

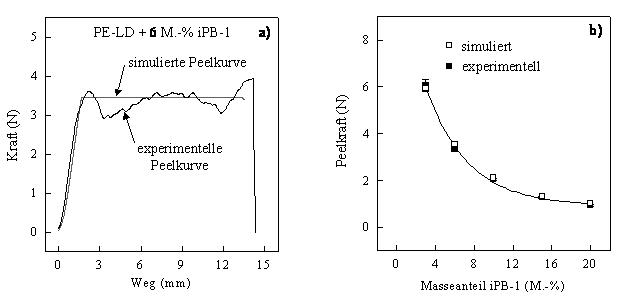
In Bild 3a ist eine aus der Finite-Elemente-Simulation errechnete Peelkurve und eine im T-Peeltest registrierte Peelkurve (siehe: Peelkraft-Bruchweg-Diagramm) exemplarisch für PE-LD mit 6 M.-% iPB-1 vergleichend dargestellt. Im Gegensatz zur experimentell ermittelten Peelkurve verläuft die simulierte Peelkurve stetig aufgrund der perfekten Trennung der entsprechenden Kohäsiv-Zonen-Elemente. Die aus der simulierten Peelkurve ermittelte Peelkraft ist in guter Übereinstimmung mit der auf experimentellen Daten basierenden Peelkraft.
Ein weiterer Unterschied der beiden Peelkurven ist am Ende des Peelvorgangs zu beobachten. Bei der auf experimentellen Werten basierenden Peelkurve wird der Peelfrontauflösungsprozess in Form einer Kraftverminderung berücksichtigt. Die simulierte Peelkurve endet abrupt, da über die Länge der Siegelnaht die kohäsiven Elemente am Ende des Peelvorgangs gleichzeitig versagen. Aufgrund dessen, dass die Peelarme nicht gelagert sind, wird die numerische Rechnung im Falle des gleichzeitigen Ablösens der letzten kohäsiven Elemente instabil und bricht ab. Dennoch ist eine zufriedenstellende Simulation des Peelvorgangs erreicht worden wie auch der Vergleich der Peelkräfte, ermittelt auf der Basis von simulierten und experimentell ermittelten Peelkurven, in Bild 3b zeigt.

Bild 3:

Simulierte und experimentell ermittelte Peelkurve für PE-LD mit 6 M.-% iPB-1 (a) und Peelkraft in Abhängigkeit vom iPB-1-Masseanteil basierend auf simulierten und experimentell ermittelten Werten (b)

Implementierung der Peelgeschwindigkeit

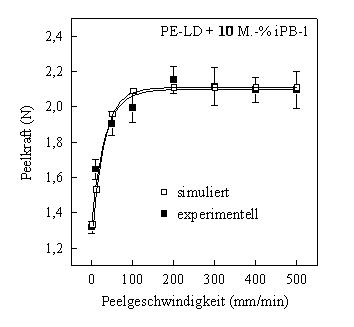
Ein weiterer Schwerpunkt der Modellierung des Peelvorgangs war die Implementierung der Peelratenabhängigkeit (Peelgeschwindigkeitsabhängigkeit) in das bestehende FE-Modell. In Bild 4 ist die Peelkraft in Abhängigkeit der Peelgeschwindigkeit für PE-LD mit 10 M.-% iPB-1 dargestellt. Die auf simulierten Werten basierende Kurve ist in guter Übereinstimmung mit den experimentellen Ergebnissen und zeigt einen exponentiellen Kurvenverlauf, der auch in anderen Studien zur Ratenabhängigkeit (Geschwindigkeitsabhängigkeit) mechanischer Eigenschaften gefunden wurde [7]. Somit wurde das FE-Modell des Peelvorgangs der PE-LD/iPB-1-Peelfolien um die Peelgeschwindigkeitsabhängigkeit erweitert.

Bild 4:

Peelkraft in Abhängigkeit der Peelgeschwindigkeit basierend auf simulierten und experimentell ermittelten Werten für PE-LD mit 10 M.-% iPB-1

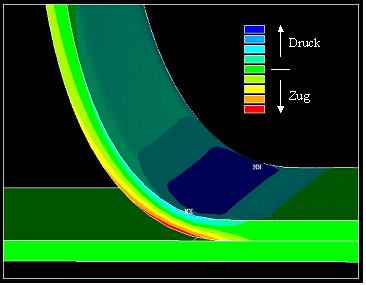
Dieses sehr komplexe FE-Modell des Peelvorgangs kann unter anderem zur Visualisierung der Spannungsverteilung im Peelprüfkörper verwendet werden (Bild 5). Es ist zu erkennen, dass beim Biegevorgang des Peelarms in der Nähe der Peelfront erwartungsgemäß sowohl Zug- als auch Druckspannungen auftreten. Im Gegensatz dazu ist im oberen Teil des Peelarms nur eine geringfügige Zugspannung zu sehen. Der über die Länge der Siegelnaht beobachtete symmetrische Spannungsverlauf macht deutlich, dass die größten Spannungen in der Mitte der Siegelnaht auftreten und somit auch dort die größte Peelgeschwindigkeit und der größte Peelfortschritt zu erwarten sind. Die im Vergleich zum Siegelnahtrand auftretende größere Spannung in der Mitte der Siegelnaht ist auf die Verformungsbehinderung an dieser Stelle zurückzuführen. In der Mitte der Siegelnaht liegt lokal der ebene Dehnungszustand (EDZ) (siehe: Ebener Spannungs- und Dehnungszustand) vor. Im Vergleich dazu kann zum Siegelnahtrand hin eine starke Verminderung der Spannung beobachtet werden. Hier herrscht keine Verformungsbehinderung, so dass die Spannungen abnehmen und daher lokal der ebene Spannungszustand (ESZ) vorliegt ¹.

---

¹ Da Folien im Allgemeinen relativ dünn sind, wird davon ausgegangen, dass in Normalenrichtung (Dickenrichtung) der Folie keine Verformungsbehinderung stattfinden kann und somit bezogen auf die gesamte Folie der ebene Spannungszustand vorliegt [8].

Bild 5:

Visualisierung der Spannungsverteilung im Peelprüfkörper und qualitative Erfassung von Zug- und Druckspannungen

Anwendung des FE-Modells

Darüber hinaus können mit dem FE-Modell des Peelvorgangs verschiedene Parameter variiert und deren Einfluss auf das Peelverhalten analysiert werden. Beispielsweise ist die Steifigkeit von Folien für verschiedene Anwendungen wie zum Beispiel Standbodenbeutel von besonderer Bedeutung. Da das PE-LD/iPB-1-Peelsystem häufig als eine funktionale Schicht innerhalb einer Mehrschichtfolie vorliegt, wird die für die Anwendung erforderliche Steifigkeit im Allgemeinen durch eine der anderen Schichten realisiert. Somit kann der Gesamt-Elastizitätsmodul der Folie je nach Anwendung, trotz des Konstanthaltens der Rezeptur und der Abmaße der Peelschicht, variieren (siehe auch: Elastizitätsmodul Beispiele Kennwertermittlung).
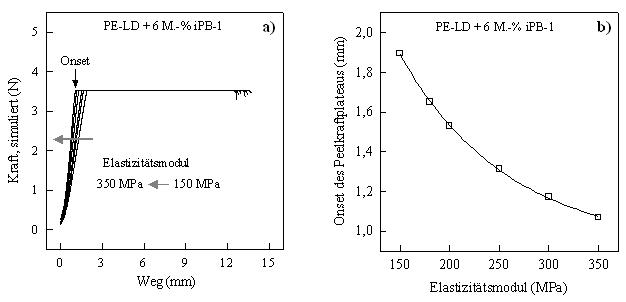
Zur Abschätzung des Einflusses unterschiedlicher Steifigkeiten auf das Peelverhalten wurde der Peelversuch exemplarisch für PE-LD mit 6 M.-% iPB-1 für unterschiedliche E-Moduln des verwendeten Peelfolienmaterials simuliert. In Bild 6a ist eine Serie von Peelkurven für Peelfolien mit unterschiedlichem E-Modul abgebildet. Trotz der Variation des E-Moduls im Bereich von 150 bis 350 MPa konnte keine Veränderung der Peelkraft festgestellt werden. Somit kann das PE-LD/iPB-1-Peelfolienblendsystem für unterschiedlichste Anwendungen eingesetzt werden und zeigt keine Veränderung der Peeleigenschaften bei variierendem E-Modul. Allerdings verändert sich der Onset des Peelkurvenplateaus in Abhängigkeit vom E-Modul (Bild 6b). Der Onset des Peelkurvenplateaus nimmt mit größer werdendem Elastizitätsmodul exponentiell ab, d. h. der Peelvorgang wird mit ansteigendem E-Modul vorzeitig initiiert. Dieser Effekt erscheint bei Betrachtung der Kohäsiv-Zonen-Elementverteilung in der Siegelnaht logisch. Mit zunehmender Steifigkeit der Folie wird der Krümmungsradius in der Nähe der Peelfront erhöht. Somit lösen sich bei erfolgter Beanspruchung mehr Elemente gleichzeitig ab als bei entsprechend kleinerem E-Modul und somit geringerem Krümmungsradius.

Bild 6:

Peelkurven für PE-LD mit 6 M.-% iPB-1 bei unterschiedlichen E-Moduln des verwendeten Peelfolienmaterials (a) und Onset des Peelkraftplateaus in Abhängigkeit des Elastizitätsmoduls (b)

Zusammenfassend kann festgestellt werden, dass das FE-Modell des Peelvorgangs eine vollständige Betrachtung des Parameterraumes ohne zusätzliche Experimente (neben denen, die zur Erstellung des FE-Modells notwendig sind) ermöglicht.

Mathematisch-statistisches Modell

Eine weitere Möglichkeit zur Modellierung des Peelvorgangs besteht in der Erstellung eines mathematisch-statistischen Modells auf Grundlage der experimentell ermittelten Abhängigkeiten [9–11]. Das mathematisch-statistische Modell beschreibt die Zusammenhänge zwischen den Ein- und Ausgangsgrößen rein mathematisch. Hierzu muss nur bedingt Kenntnis über die zu Grunde liegenden physikalischen Zusammenhänge bestehen. Zum Aufstellen des statistischen Modells werden zunächst die notwendigen Ein- und Ausgangsgrößen festgelegt und anschließend die zugehörigen Abhängigkeiten experimentell ermittelt. Danach wird die entsprechende Berechnungsgleichung formuliert, die neben den Eingangsgrößen als Variablen noch zu bestimmende, das Modell kalibrierende, Faktoren enthält. Als Nachteil der statistischen Modellbildung ist zu nennen, dass sich die ermittelten Berechnungsgleichungen in der Regel lediglich auf das beobachtete Prozessfenster der gemessenen Eingangsgrößen beziehen und nicht ohne Weiteres auf andere ähnliche Eingangsgrößen übertragbar sind.

Werden die Maschinenparameter als Eingangsgrößen eines statistischen Modells gewählt, so wäre das Modell auf die Blasfolienanlage beschränkt, auf der es ermittelt worden ist. In einem solchen Fall wäre das statistische Modell nicht übertragbar und somit nicht allgemein gültig. Werden hingegen die maschinenunabhängigen Prozessparameter als Eingangsgrößen eines statistischen Modells gewählt, so bildet das Modell den Zusammenhang zwischen Prozesszustand und Peelverhalten ab. Ein derartiges statistisches Modell wäre bezüglich der Blasfolienanlage allgemein gültig und übertragbar, jedoch an das entsprechende Material und seine chemische Struktur gebunden.

Am Beispiel des PE-LD/iPB-1-Peelfolienblendsystems wird der Zusammenhang zwischen den maschinenunabhängigen Prozessparametern als Eingangsgröße und der Peelkraft als Ausgangsgröße formuliert. Hierbei wird von der als optimal ermittelten Rezeptur PE-LD mit 6 M.-% iPB-1 ausgegangen. Das Modell berücksichtigt die sich infolge polymorpher Kristallumwandlung von iPB-1 verändernde Peelkraft [12]. Darüber hinaus wird vorausgesetzt, dass die entsprechenden Peelfolien bei Standardsiegelparametern gesiegelt wurden (siehe: Siegelnaht). Somit wird das Peelverhalten nach Gl. (3) berechnet.

$F_{peel}\,=\,F_{peel}^{MW6}\,+\,f\left(AZV\right)\,-\,F_{peel,AZV}\,+\,f\left(t_{E}\right)\,-\,F_{peel,t_{E}}\,$ $+\,f\left(T_{S}\right)\,-\,F_{peel,T_{S}}+\,f\left(ABV\right)\,-\,F_{peel,ABV}\,+\,f\left(t\right)\,-\,F_{peel,t}$

(3)

mit

$F_{peel}^{MW6}$		Mittelwert der Peelkräfte bei Standardprozess- und Standardsiegelparametern aus den jeweils untersuchten Abhängigkeiten für PE-LD mit 6 M.-% iPB-1
f(AZV)		funktionaler Zusammenhang zwischen Peelkraft und Abzugsverhältnis (AZV)
Fpeel,AZV		Peelkraft bei Standard-AZV
f(tE)		funktionaler Zusammenhang zwischen Peelkraft und Einfrierzeit
Fpeel,tE		Peelkraft bei Standard-Einfrierzeit
f(TS)		funktionaler Zusammenhang zwischen Peelkraft und Temperatur der Schmelze
Fpeel,TS		Peelkraft bei Standard-Temperatur der Schmelze
f(ABV)		funktionaler Zusammenhang zwischen Peelkraft und Aufblasverhältnis (ABV)
Fpeel,ABV		Peelkraft bei Standard-ABV
f(t)		funktionaler Zusammenhang zwischen Peelkraft und Zeit nach dem Siegeln
Fpeel,t		Peelkraft bei Standardkonditionierungszeit (im Allgemeinen 10 Tage)

Alle aufgeführten Abhängigkeiten haben einen gemeinsamen Messpunkt der Peelkraft bei dem jeweiligen Standardparameter. Im Idealfall ist davon auszugehen, dass die entsprechenden Peelkräfte bei Standardparametern identische Werte aufweisen, so dass sich Gl. (3) unter Berücksichtigung eines Kalibrierfaktors bzw. Kalibrierterms K zu Gl. (4) vereinfacht.

$F_{peel}\,=\,f\left(AZV\right)\,+\,f\left(t_{E}\right)\,+\,f\left(T_{S}\right)\,+\,f\left(ABV\right)\,$ $+\,f\left(t\right)\,-\,4\,F_{peel}^{MW6}\,+\,K$

(4)

Der Kalibrierterm wurde mit K = 0,0985 N ermittelt.

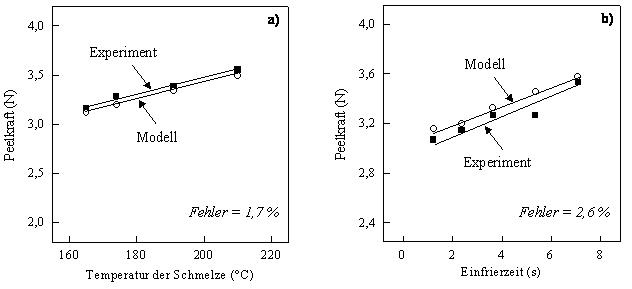
Zur Überprüfung des vorgestellten mathematisch-statistischen Modells wurden experimentelle Ergebnisse mit errechneten Werten auf Basis des Modells verglichen. In Bild 7a ist die Peelkraft in Abhängigkeit der Temperatur der Schmelze zu sehen. Die mit Hilfe des mathematisch-statistischen Modells errechneten Peelkraftwerte stehen in guter Übereinstimmung mit den experimentellen Ergebnissen. Der durch das Modell hervorgerufene mittlere Fehler beträgt lediglich 1,7 %. Auch die in Bild 7b dargestellte Abhängigkeit der Peelkraft von der Einfrierzeit zeigt eine gute Übereinstimmung zwischen experimentellen und errechneten Werten, so dass der durch die Modellierung gemachte mittlere Fehler nur 2,6 % beträgt.

Bild 7:

Peelkraft als Funktion der Temperatur der Schmelze (a) und der Einfrierzeit (b) für PE-LD mit 6 M.-% iPB-1, basierend auf experimentellen Daten und dem mathematisch-statistischen Modell; die übrigen Prozessparameter haben Standard-Werte.

Das vorgeschlagene mathematisch-statistische Modell ist somit erfolgreich überprüft worden und gibt sehr genau die physikalischen Zusammenhänge wieder. Es kann daher auch für weitere, experimentell noch nicht ermittelte, Parametervariationen verwendet werden.
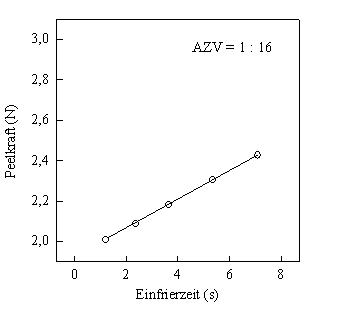
Auf Grundlage des Modells wird nachfolgend der Einfluss der Einfrierzeit auf die Peelkraft bei einem Abzugsverhältnis von 1:16 ermittelt bzw. prognostiziert. Die entsprechende Abhängigkeit ist in Bild 8 dargestellt. Aufgrund des erhöhten Abzugsverhältnisses kann bei niedrigen Einfrierzeiten eine Peelkraft von rund 2 N realisiert werden. Das entspricht unter Zugrundelegung der Abhängigkeit der Peelkraft vom iPB-1-Masseanteil einem iPB-1-Gehalt von 10 M.-%. Somit kann in der Praxis der Masseanteil an iPB-1 von 10 M.-% auf 6 M.-% gesenkt werden und bei entsprechender Prozessparametervariation bleibt die Peelkraft auf dem Niveau von 10 M.-% iPB-1 erhalten (vgl. Bild 8).

Bild 8:

Peelkraft in Abhängigkeit der Einfrierzeit, bei einem AZV von 1:16, berechnet nach dem mathematisch-statistischen Modell; die übrigen Prozessparameter haben Standard-Werte

Davon ausgehend, dass die Kosten für iPB-1 derzeit etwa 3-mal höher als für PE-LD sind, würde eine Verminderung des iPB-1-Masseanteils im PE-LD/iPB-1-Peelfolienblendsystem von 10 M.-% iPB-1 auf 6 M.-% iPB-1 eine Gesamtkostenersparnis von 7 % ausmachen.
Das vorgestellte mathematisch-statistische Modell bietet eine komfortable Möglichkeit der Modellierung des Peelverhaltens auf Basis der ermittelten experimentellen Abhängigkeiten. Unter Verwendung des Modells können Prognosen zur Abhängigkeit der Peelkraft von den Prozessparametern erstellt werden, die jedoch nur innerhalb der verwendeten Variationsgrenzen der Prozessparameter gültig sind. Darüber hinaus ist das Modell auch für Prognosen auf anderen Blasfolienanlagen bei Verwendung der gleichen Peelfolienmaterialien übertragbar, da dem Modell ausschließlich maschinenunabhängige Prozessparameter zugrunde liegen.

Literaturhinweise

[1]	Nase, M.: Zusammenhang zwischen Herstellungsbedingungen, übermolekularer Struktur und Eigenschaften von Peelfolien. Shaker Verlag, Aachen (2010) (ISBN 978-3-8322-9099-3; siehe AMK-Büchersammlung unter B 1-17)
[2]	Needleman, A.: A Continuum Model for Void Nucleation by Inclusion Debonding. J. of Appl. Mechan. 54 (1987) 525–531
[3]	Sargent, J. P.: Durability Studies for Aerospace Applications using Peel and Wedge Tests. International Journal of Adhesion and Adhesives 25 (2005) 247–256
[4]	Geißler, G., Kaliske, M.: A Cohesive Element Approach for Viscoelastic Interface Properties. Proceedings in Applied Mathematics and Mechanics 4 (2004) 187–188
[5]	Gerlach, S., Fiolka, M., Matzenmiller, A.: Modeling and Analysis of Adhesively Bonded Joints with Interface Elements for Crash Analysis. LS-DYNA Anwenderforum Bamberg (2005) Tagungsband S. 35–44
[6]	Geißler, G., Kaliske, M., Nase, M., Grellmann, W.: Peel Process Simulation of Polymeric Films – Computational Modeling of Experimental Results. Engineering Computations 24 (2007) 586–607 [Gewinner des “Outstanding Paper Award” 2008 des Emerald Literati Network.]
[7]	Schoßig, M., Bierögel, C., Grellmann, W., Bardenheier, R., Mecklenburg, T.: Effect of Strain Rate on Mechanical Properties of Reinforced Polyolefins. European Conference of Fracture (ECF 16) Alexandroupolis Greece (2006) Conference Proceedings Section P 1–6
[8]	Anderson, T. L.: Fracture Mechanics. Fundamental and Applications. CRC Press, Boca Raton (2005) (ISBN 978-0-8493-1656-2; siehe AMK-Büchersammlung unter E 8-2)
[9]	Ohlendorf, F.: Vorhersagen der mechanischen Folieneigenschaften bei der Schlauchfolienextrusion. Dissertation, Rheinisch-Westphälische Hochschule Aachen (2004)
[10]	Ahrens, H., Bellmann, K.: Ein mathematisch-statistisches Modell polygener Modifikatorsysteme. Biometrische Zeitschrift 12 (2007) 113–126
[11]	Reinsch, E. A. (Hrsg.): Mathematik für Chemiker. Vieweg+Teubner Verlag, Wiesbaden (2004)
[12]	Nase, M., Androsch, R., Langer, B., Baumann, H. J., Grellmann, W.: Effect of Polymorphism of Isotactic Polybutene-1 on Peel Behavior of Polyethylene/Polybutene-1 Peel Systems. Journal of Applied Polymer Science 107 (2008) 3111–3118