Ultraschall-Elastische Kennwerte
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Ultraschall – Elastische Kennwerte
Ermittlung der elastischen Kennwerte mit Ultraschall
Allgemeines
Die Ermittlung elastischer Kennwerte mittels der Ultraschallmesstechnik ist eine Messmethode der zerstörungsfreien Kunststoffprüfung, welche unter bestimmten Voraussetzungen genauere Ergebnisse im Vergleich zum Zugversuch mit Längs- und Querdehnungsaufnehmern besitzt, als dies in der Materialprüfmaschine mit mechanischen oder optischen Dehnungsaufnehmern möglich ist. Daneben ist diese Methode sehr wirtschaftlich, weil sie nicht nur zerstörungsfrei, sondern auch verhältnismäßig schnell durchzuführen ist.
Die Berechnungsgleichungen des Elastizitätsmoduls, des Schubmoduls, des Kompressionsmoduls und der Querkontraktionszahl (Poissonzahl) ergeben sich aus der Elastizitätstheorie, welche die Massendichte sowie die longitudinalen und transversalen Schallgeschwindigkeiten des geprüften Werkstoffes enthalten [1].
Diese Gleichungen gelten exakt für Werkstoffe mit linear-elastischem Verhalten wie z. B. Metalle und Keramiken und sind daher nur näherungsweise auch für heterogene Werkstoffe verwendbar. Für Kunststoffe ist zu beachten, dass aufgrund ihrer Viskoelastizität – und auch der Heterogenität der teilkristallinen Polymere (siehe: Kristallinität) – generell mit einer hohen Schalldämpfung zu rechnen ist und stärkere Streuungen bei den Messreihen auftreten [2] (siehe auch: Absorption_Schallwellen). Aus diesem Grunde sind für diese Werkstoffe niedrigere Messfrequenzen einzusetzen, wobei die Inhomogenitäten um ein Mehrfaches kleiner als die Wellenlänge sein sollen, damit die Berechnungsgleichungen, wie unten aufgeführt, noch gültig sind.
Prüfkörper
Für die Durchführung der Messungen ist eine spezielle Geometrie von Prüfkörpern nötig, welche eine genaue Ermittlung der longitudinalen und transversalen Schallgeschwindigkeiten erlaubt. In der folgenden Abbildung (Bild 1) ist eine mögliche Geometrie dargestellt.
| Bild 1: | Prismatischer Prüfkörper mit Schrägschliff |
Die Geometrie eines Quaders ermöglicht die Messung beider Schallgeschwindigkeiten, wobei der Schrägschliff an die Richtung des vom Winkelprüfkopf einfallenden Schallstrahles (der Hauptachse des sich ausbildenden Schallfeldes) angepasst ist (vgl. Bild 2b). Diese Anpassung erfolgt so, dass die Transversalwelle (siehe auch: Brechung Schallwellen) senkrecht auf den Schrägschliff trifft.
Messung der Schallgeschwindigkeiten
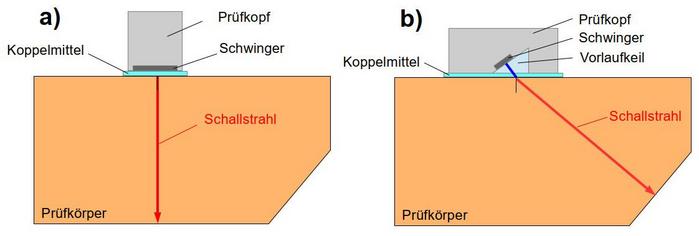
Für die Messung der longitudinalen Schallgeschwindigkeit cL wird mit einem Normalprüfkopf (auch als Senkrecht-Prüfkopf bezeichnet) nach dem Impuls-Echo-Verfahren vorgenommen. Er wird an den Prüfkörper (nach Bild 2a) so angekoppelt, dass die Hauptachse (= akustische Achse) des sich ausbildenden Schallfeldes senkrecht auf die zwei gegenüberliegenden planparallele Oberflächen des Prüfkörpers trifft. Damit sind die akustischen Achsen der Schallfelder des hinlaufenden und von der Wand zurücklaufenden Schallstrahls gleich und die Schallgeschwindigkeit kann über die Formel
| (1) |
berechnet werden. Innerhalb der Zeit ts (Schalllaufzeit) durchläuft die Schallwelle die doppelte Dicke d.
| Bild 2: | Prismatischer Prüfkörper mit Schrägschliff und Ankopplung eines Normal- (a) und eines Winkelprüfkopfes (b) |
Zur Messung der transversalen Schallgeschwindigkeit cT wird der Winkelprüfkopf so ausgerichtet, dass der Schallstrahl, also die Hauptachse des Schallfeldes, senkrecht auf die schräg geschliffene Fläche trifft (Bild 2b). Die Ermittlung der transversalen Schallgeschwindigkeit erfolgt nach Gleichung (1) völlig analog.
Ermittlung der elastischen Kennwerte
Die Module des Werkstoffes (Elastizitäts (E)-, Schub (G)-, Kompressions (K)- Modul) sowie die Querkontraktionszahl µ ergeben sich aus den Beziehungen zwischen den linear-elastischen Kennwerten und der Dichte ρ sowie der Schallgeschwindigkeit. Sie besitzen die folgende Form:
| (2) |
| (3) |
| (4) |
| (5) |
Diese Beziehungen gelten strenggenommen für isotrope feste Körper. So sind diese Gleichungen exakt gültig für homogene (nicht-poröse) Keramiken [3]. Sie können aber auch in guter Näherung zur Bestimmung der elastischen Eigenschaften an heterogenen Werkstoffen verwendet werden. Das ist immer dann der Fall, wenn die Inhomogenitäten (siehe Kategorie: Schadensanalyse Bauteilversagen) in den Werkstoffen klein gegenüber der Wellenlänge sind, mit der sich Ultraschallwellen im Material ausbreiten.
Bemerkungen zur Genauigkeit des Verfahrens
Die Struktur des Schallfeldes ist bei Normal- und Winkelprüfköpfen unterschiedlich. So weist der Normalprüfkopf ein axialsymmetrisches Schallfeld auf, welches sich mit zunehmender Nennfrequenz des Prüfkopfes verjüngt. Damit ist eine sehr genaue Messung der Schallgeschwindigkeit möglich, wenn sowohl die Oberfläche, auf welcher der Prüfkopf aufgesetzt wird, als auch die angeschallte Grenzfläche (siehe Phasengrenzfläche) normal zur Schallfeldachse liegt. Hierbei empfiehlt sich, wenn die Schalldämpfung nicht zu hoch ist, die Mehrfachechomethode (siehe Ultraschall-Wanddickenmessung).
Die Ungenauigkeiten treten eher mit dem Winkelprüfkopf auf, dessen Schallfeld einen größeren Divergenzwinkel (siehe Ultraschall-Normal-Prüfköpfe) besitzt. Damit ist nach dem Abstandsgesetz I = I0 ⋅ r^(-2) die reflektierte Amplitude der vom Winkelprüfkopf ausgesandten Welle signifikant geringer als beim Normalprüfkopf. Hierbei stellt I0 die Intensität des vom Prüfkopf ausgesandten, I diejenige der empfangenen Welle und r den doppelten Abstand zwischen Prüfkopf und reflektierender Fläche dar. Diese Schallschwächung ist demnach beim Winkelprüfkopf größer. Zudem sind Winkelprüfköpfe in ihrer Nennfrequenz beschränkt auf maximal 5 MHz [4], womit sich nicht die gleiche Genauigkeit erreichen lässt, wie beim Normalprüfkopf (≥ 10 MHz). Deshalb sollte zur Messung der transversalen Schallgeschwindigkeit der Winkelprüfkopf zunächst kalibriert werden.
Literaturhinweise
| [1] | Landau, L. D., Lifschitz, E. M.: Lehrbuch der theoretischen Physik – Elastizitätstheorie Bd. 7, Akademieverlag Berlin (2009) |
| [2] | Krautkrämer, J., Krautkrämer, H.: Die Schwächung von Ultraschallwellen in festen Stoffen. In: Krautkrämer, J., Krautkrämer, H. (Hrsg.): Werkstoffprüfung mit Ultraschall. Springer Verlag Berlin, Heidelberg (1986) (ISBN 978-3-662-10909-0) |
| [3] | DIN EN 843-2 (2007): Hochleisungskeramik – Mechanische Eigenschaften monolithischer Keramik bei Raumtemperatur – Teil 2: Bestimmung des Elastizitätsmoduls, Schubmoduls und der Poissonzahl |
| [4] | Waygate Technologies – Baker Hughes Company.: Ultraschallprüfköpfe für Fehlernachweise und Größenbestimmungen. Baker Hughes Company (2020) https://www.bakerhughesds.com/sites/g/files/cozyhq596/files/2020-07/bhcs34592-de_ultrasonic_transducers_catalog_r9.pdf (Zugriff am 06.02.2023) |