Korrespondenzprinzip

Ein Service der
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung
PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Korrespondenzprinzip

Einordnung

Das Korrespondenzprinzip leitet sich aus dem BOLTZMANN’schen Superpositionsprinzip ab. Es liefert die für die Praxis wichtige Aussage, dass die von Seiten der Elastizitätstheorie vorliegenden Lösungen im linear-viskoelastischen Bereich genutzt werden dürfen. Voraussetzung hierfür ist, dass die viskoelastischen Deformationen bei konstruktiv genutzten Kunststoffen sehr klein sind. Da diese Lösungen die Basis aller Festigkeitsrechnungen sind, bedeutet das für den Einsatz der Kunststoffe eine große Erleichterung.

Grundlagen Korrespondenzprinzip

Es wird lediglich an Stelle der Spannungen σ die zeitabhängige Spannungsfunktion σ(t), an Stelle der Deformation ε die zeitabhängige Deformation ε(t) und an Stelle des E-Moduls den Relaxationsmodul E_r(t) bzw. den Kriechmodul (siehe: Kriechverhalten Ermittlung) eingesetzt. An Stelle des Relaxations- bzw. Kriechmoduls arbeitet man jedoch meist mit dem Kehrwert, der Nachgiebigkeit C(t) = 1/ E_r(t) (C...Compliance).

Dies gilt natürlich auch für jeden anderen Modul (Schub- und Kompressionsmodul), jede andere Spannung und jede andere Deformation. Die zeitabhängigen Größen stehen untereinander mit den aus der Elastizitätstheorie bekannten Beziehungen in Verbindung, wobei zusätzlich die Zeitabhängigkeit der Querkontraktion zu berücksichtigen ist.

Zeit- und Temperaturabhängigkeit von Modul und Poissonzahl

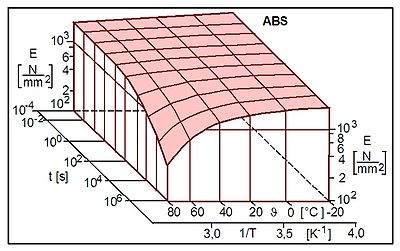
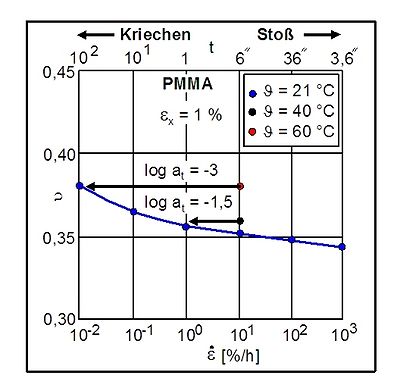
Die nachfolgenden Beispiele zeigen die Zeit- und Temperaturabhängigkeit des Moduls von Acrylnitril-Butadien-Styrol (Kurzzeichen: ABS) sowie die Zeitabhängigkeit der Querkontraktionszahl am Beispiel von Polymethylmethacrylat (Kurzzeichen: PMMA).

Bild:

Zeit- und Temperaturabhängigkeit des Elastizitätsmoduls für ABS nach Menges

Bild:

Querkontraktionszahl in Abhängigkeit von der Dehnungsgeschwindigkeit ${\dot {\varepsilon }}$von PMMA bei einachsiger Deformation nach Menges

Siehe auch

• Elastizität
• Linear-viskoelastisches Verhalten
• BOLTZMANN'sches Superpositionsprinzip
• Zeit-Temperatur-Superpositionsprinzip

Literaturhinweis

• Menges, G.: Werkstoffkunde Kunststoffe. 3., völlig neu überarb. und erweiterte Auflage, Carl Hanser Verlag, München Wien (1990) S. 121, (ISBN 978-3-446-15612-8; siehe AMK-Büchersammlung unter G 11)