CIELAB-Farbraum
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
CIELAB-Farbraum
CIE 1976 L*a*b*-Farbraum (CIELAB)
Zur reproduzierbaren Bestimmung der Farbe hat die internationale Beleuchtungskommission CIE (Commission Internationale de l'Éclairage, Wien, Österreich) im Jahr 1976 den L*a*b*-Farbraum, einen dreidimensionalen, annähernd gleichabständigen Farbraum eingeführt, wobei die Größen L*, a* und b* nach Gl. (1) bis (6) ermittelt [1] und in ein kartesisches Koordinatensystem eingetragen werden [1–3]. Die Größe L* entspricht der Helligkeit, a* wird als Rot-Grün-Buntheit und b* als Gelb-Blau-Buntheit bezeichnet. Werden die Größen a* und b* in Polarkoordinaten nach Gl. (7) und Gl. (8) umgerechnet, dann wird häufig vom LCh-Farbraum gesprochen, wobei es sich allerdings um den L* a* b*-Farbraum einzig unter Darstellung der Polarkoordinaten handelt. In der Literatur wird üblicherweise für den L*a*b*-Farbraum die Abkürzung CIELAB-Farbraum, manchmal auch CIELAB 1976, verwendet. Die Helligkeit L* wird unter Festlegung eines idealen Weißstandards (üblicherweise Bariumsulfat BaSO4) auf den Wertebereich Null (0) bis 100 begrenzt und Weiß besitzt dabei den Zahlenwert 100.
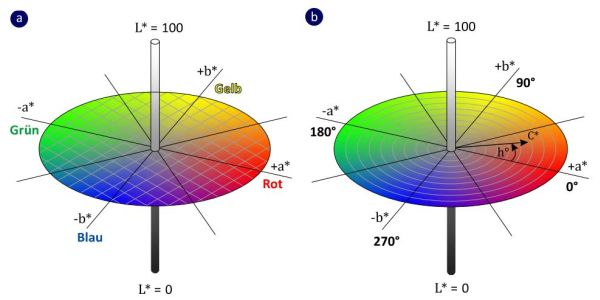
| Bild 1: | Schematische Darstellung des CIELAB-Farbraumes im kartesisches Koordinatensystem (L*, a*, b*) (a) sowie im Polarkoordinatensystem (L*, C*ab, hab) (b); Bilder in Anlehnung an [4] |
Bild 1a und b zeigt graphisch die mathematischen Zusammenhänge des CIELAB-Farbraums. Die Farbmaßzahl C*ab wird als Buntheit (CIELAB chroma) und hab als Bunttonwinkel (CIELAB hue angle) bezeichnet. Für den Buntton hab werden die Annahmen getroffen, dass Winkel zwischen 0° und 90° erhalten werden, wenn sowohl a* wie auch b* positiv sind. Dagegen nimmt der Winkel Werte zwischen 90° und 180° an, wenn a* negativ und b* positiv ist. Ist sowohl a* und b* negativ, werden Werte zwischen 180° und 270° erhalten und falls a* positiv und b* negativ ist, liegen die Winkel im Bereich von 270° und 360°. Für unbunte Farben ist die Buntheit C*ab gleich Null (vgl. Bild 1b).
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle L*=116\cdot f_{y}-16} | (1) |
| Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a*= 500 \cdot (f_{x}-f_{y})} | (2) |
| Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b*= 200 \cdot (f_{y}-f_{z})} | (3) |
| Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_{x}= \frac{841}{108}\cdot \left ( \frac{X}{X_{n}} \right )+\frac{16}{116}\ \mathrm{wenn}\ \left ( \frac{X}{X_{n}} \right )\leq \left ( \frac{24}{116} \right )^{3},\ \mathrm{sonst}\ f_{x}=\sqrt[3]{\frac{X}{X_{n}}}} | (4) |
| Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_{y}= \frac{841}{108}\cdot \left ( \frac{Y}{Y_{n}} \right )+\frac{16}{116}\ \mathrm{wenn}\ \left ( \frac{Y}{Y_{n}} \right )\leq \left ( \frac{24}{116} \right )^{3},\ \mathrm{sonst}\ f_{y}=\sqrt[3]{\frac{Y}{Y_{n}}}} | (5) |
| Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_{z}= \frac{841}{108}\cdot \left ( \frac{Z}{Z_{n}} \right )+\frac{16}{116}\ \mathrm{wenn}\ \left ( \frac{Z}{Z_{n}} \right )\leq \left ( \frac{24}{116} \right )^{3},\ \mathrm{sonst}\ f_{z}=\sqrt[3]{\frac{Z}{Z_{n}}}} | (6) |
| Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle C^{*}_{ab}=\sqrt{a^{*2}+b^{*2}}} | (7) |
| Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h_{ab}=\arctan \frac{b^{*}}{a^{*}}} | (8) |
Die Größen X, Y, Z in den Gl. (4) bis Gl. (6) sind die Farbwerte des Proben-Farbreizes auf der Grundlage des Normvalenzsystemes CIE 1931 (2°-Normalbeobachter) und Xn, Yn, und Zn die entsprechenden Farbwerte eines festgelegten weißen Farbreizes. Das Normvalenzsystem CIE 1964 beschreibt einen 10°-Normalbeobachter und zur Unterscheidung werden die Größen X10, Y10 und Z10 definiert, wobei eine Substitution der Größen X, Y, Z in den Gl. (4) bis Gl. (6) erfolgt.
Literaturhinweise
| [1] | Hunt, R. W. G.: The Reproduction of Colour. John Wiley & Sons Ltd, The Atrium, Southern Gate, Chichester, West Sussex PO19 8SQ, England, 2004. |
| [2] | DIN EN ISO/CIE 11664-4 (2020-03): Farbmetrik – Teil 4: CIE 1976 L* a* b* Farbraum. |
| [3] | Schanda, J. (Ed.), Colorimetry: Understanding the CIE System. John Wiley & Sons, Inc., Hoboken, New Jersey, 2007. |
| [4] | Grundlagen der Farbmetrik. Seminarprogramm „Praktische Farb- und Glanzmessung” der BYK-Gardner GmbH, 27. September 2011 |