Rissmodell nach BARENBLATT

Ein Service der
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung
PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Rissmodell nach BARENBLATT

Grundlagen des Modells

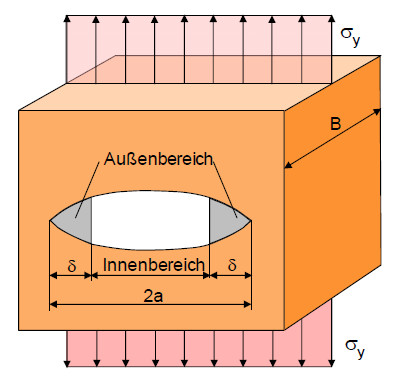
Den Rissmodellen von GRIFFITH und IRWIN & Mc CLINTOCK ist gemeinsam, dass es bei einem sehr scharfen Kerb an der Spitze eines Risses zum Auftreten unendlich großer Spannungen kommt. Um diese zwischen den Modellvorstellungen und den praktisch möglichen Verhältnissen entstehende Diskrepanz zu beseitigen, wurde von Barenblatt ein Modell zur elastizitätstheoretischen Beschreibung der Spannungsverhältnisse an der Rissspitze entwickelt (Bild 1). Dabei wird der Riss in einen Innen- und zwei Außenbereiche unterteilt.

Bild 1:

Rissmodell nach BARENBLATT

Bei dem Rissmodell von Barenblatt werden atomare bzw. molekulare Kohäsivkräfte angenommen, die zu einem glatten Schließen der Rissflächen führen.

Der Riss öffnet sich dabei im Außenbereich δ kontinuierlich, die Interpretation erfolgt dahingehend, dass sich die Atom- und Molekülabstände im Bereich δ kontinuierlich vergrößern und dabei eine Wechselwirkung in Form von Kohäsionskräften wirkt. Diese können die theoretische Festigkeit des Werkstoffes erreichen.
(Kohäsion: Zusammenhalt der Moleküle eines Körpers)

Kohäsionskräfte und Kohäsionsmodul

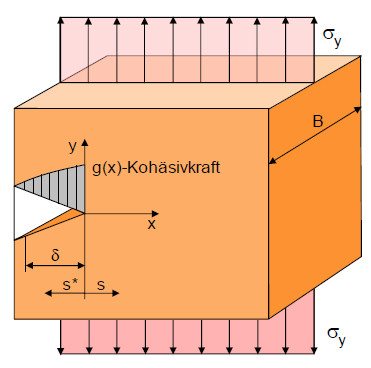
Im Bild 2 ist der Verlauf der Kohäsionskräfte und der sich daraus ergebenden Spannungen in x-Richtung über die Risslänge aufgetragen.

Bild 2:

Spannungsverlauf an der Rissspitze nach Barenblatt

Als Werkstoffkenngröße formulierte Barenblatt das Integral der Verteilung der Kohäsionskräfte über den Rissquerschnitt und bezeichnete es als Kohäsionsmodul

$B=\int _{0}^{\delta }{\frac {g(s^{*})ds^{*}}{\sqrt {s^{*}}}}$ oder: $B=\int _{0}^{\delta }{\frac {g(x)}{\sqrt {x}}}dx$

mit

s*		Koordinate in x-Richtung
g		Kohäsionskraft

Obwohl eine Reihe von Verfahren zur Berechnung des Kohäsionsmoduls vorgeschlagen wurden, bleibt eine genaue Bestimmung dieser Kenngröße problematisch.

Der Vorteil der BARENBLATT’schen Modellvorstellung besteht darin, dass die beim Rissmodell von GRIFFITH an der Rissspitze auftretenden unendlich großen Spannungswerte vermieden werden und mögliche Verteilungen der Spannung an einem unendlich scharfen Riss beschrieben werden.

In den letzten Jahren ist jedoch ein verstärktes Interesse an diesem, auch als Kohäsivzonenmodell bezeichnetem, Rissmodell zu verzeichnen. Das ist auch, neben der Erweiterung des Modells selbst, durch die immensen Fortschritte der Rechentechnik bedingt.

Anwendungsbereich

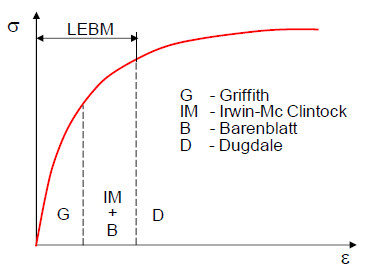
Bild 3:

Gültigkeitsbereich der Rissmodelle

Bedeutung

Diese Theorie hatte in der Praxis lange Zeit relativ wenig Anwendung gefunden. Es gibt Anwendungsbeispiele u. a. bei der Analyse von:

• geologischen Bruchvorgängen
• der Spannungsrisskorrosion von Polymeren
• der Rissausbreitung an Grenzflächen / in Grenzschichten (interlaminare Rissausbreitung, Rissausbreitung in Kleb- und Schweißverbindungen etc.)

Literaturhinweise

Grundlagen:

• Barenblatt, G. I.: Prikl. Math. i. Mech. XX, 4 (1956), S. 475. In: Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig (1987) 2. Auflage S. 22 ISBN 3-342-00096-1; siehe AMK-Büchersammlung unter E 29-2)
• Barenblatt, G. I.: The Formation of Equilibrium Cracks During Brittle Fracture. General Ideas and Hypotheses. Axially-symmetric Cracks. Journal of Applied Mathematics and Mechanics 23 (1959) 622–636
• Barenblatt, G. I.: Equilibrium Cracks Formed During Brittle Fracture Rectilinear Cracks in Plane Plates. Journal of Applied Mathematics and Mechanics 23 (1959) 1009–1029
• Barenblatt, G. I.: Concerning Equilibrium Cracks Forming During Brittle Fracture. The Stability of Isolated Cracks. Relationships with Energetic Theories. Journal of Applied Mathematics and Mechanics 23 (1959) 1273–1282
• Barenblatt, G. I.: The Mathematical Theory of Equilibrium Cracks in Brittle Fracture. Adv. in Appl. Mech. 7 (1962) 55

Anwendungen (Auswahl):

• Marzi, S. H.: Ein ratenabhängiges, elasto-plastisches Kohäsivzonenmodell zur Berechnung struktureller Klebeverbindungen unter Crashbeanspruchung. Fraunhofer IFAM, Bremen (Hrsg.), Fraunhofer Verlag, Stuttgart (2010)
• Scheider, I.: Bruchmechanische Bewertung von Laserschweißverbindungen durch numerische Rissfortschrittsimulation mit dem Kohäsivzonenmodell. GKSSForschungszentrum Geesthacht (2001)
• Yuan, H., Cornec, A., Schwalbe, K.-H.: Numerische Simulation duktilen Risswachstums mittels Kohäsivzonenmodells an dünnen Aluminium-CT-Proben