Objekt-Rasterverfahren
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Objekt-Rasterverfahren
Grundlagen des Messverfahrens
Methodisch und messtechnisch ist das Objekt-Rasterverfahren den optischen Feldmesstechniken zur Darstellung von Verschiebungs-, Dehnungs- und Spannungsfeldern von Prüfobjekten zuzuordnen. Damit können diese optischen Messtechniken großflächig, berührungslos und rückwirkungsfrei wesentliche Informationen zur Form- bzw. Gestaltsänderung und Spannungsverteilung komplizierter und komplexer Bauteile als auch von Prüfkörpern unter mechanischer und/oder thermischer sowie medialer Beanspruchung geben, die dann zur Verifizierung von FEM-Daten oder zur Überprüfung konstruktiver Details genutzt werden können [1–3]. Neben dieser Messtechnik können vergleichbare Ergebnisse mit dem Raster-Reflexionsverfahren, der Laser-Speckle-Interferometrie (ESPI), der Laserextensometrie, Holografie und der Shearographie erzielt werden.
Das Objekt-Rasterverfahren ist eine vergleichsweise einfache Prüfmethode zur Erfassung der lokalen und integralen Verformungen von Bauteil- oder Prüfkörperoberflächen, die zur Beurteilung der Bauteildimensionierung, der Überprüfung von FEM-Berechnungen und für die zerstörungsfreie Werkstoffprüfung genutzt werden kann. Dabei können je nach Ausstattungsgrad des Prüfsystems die flächenhaften Verschiebungen u und v in x- und y-Richtung (in-plane bei 2d) als auch von w-Verschiebungen (out-of-plane bei 3d) in z-Richtung ausgewählter Oberflächenmerkmale in Echtzeit ermittelt und zur Berechnung der jeweiligen Verschiebungsvektoren und Dehnungsverteilungen verwendet werden. Bei Verwendung von nur einer CCD-Kamera kann nur in-plane gemessen werden, wobei die Verschiebungen in x- und y- Richtung erfasset werden. Bei zwei CCD-Kameras die im Winkelbereich von ca. 20 bis 60° bezüglich des Prüfobjekts angeordnet sind, kann über Triangulationsalgorithmen zusätzlich die Verschiebung w in der z-Richtung ermittelt werden. Falls Informationen über das Verformungsverhalten der Rückseite des Prüfobjekts erforderlich sind, können je nach Ausstattungsgrad des Messsystems insgesamt bis zu 5 (teilweise auch bis zu 8) CCD-Kameras appliziert werden.
In Abhängigkeit von den Eigenschaften der eingesetzten CCD-Kameras (Anzahl der Pixel, Signaltiefe in Bit, Messfrequenz) sind somit messtechnische Anwendungen im statischen bzw. quasistatischen Belastungsfall bis hin zu schwingenden Belastungen oder Hochgeschwindigkeitsprüfungen (Crash- oder CAI-Test) an beliebigen Prüfobjektgeometrien realisierbar (siehe: Schlagbeanspruchung Kunststoffe und Schlagbeanspruchung Hochgeschwindigkeitsprüfung), wobei auftretende Festkörperverschiebungen infolge von Objektbewegungen berücksichtigt werden können.
Damit können mit diesem berührungslosen Prüfverfahren je nach verwendeter Kamera und Messanordnung folgende Prüfaufgaben wahrgenommen werden:
- Ermittlung von drei- oder zweidimensionalen Verschiebungsfeldern,
- Bestimmung der zugehörigen in-plane- und out-of-plane Dehnungsfelder,
- Ermittlung des Verformungsverhaltens von Werkstoffen oder Kunststoffen und gefügten Bauteilen sowie Messung der Objektkontur,
- Verifizierung von FEM-Berechnungen zum Bauteilverhalten unter diversen Beanspruchungen,
- Spannungsverteilung und Festigkeitsnachweis mittels bestimmten Dehnungsfeld und einem geeigneten Stoffgesetz und
- Bestimmung von Werkstoffverhalten und -kennwerten, wie Poissonzahl, Spannungsüberhöhung oder lokalen Elastizitätsmodulen.
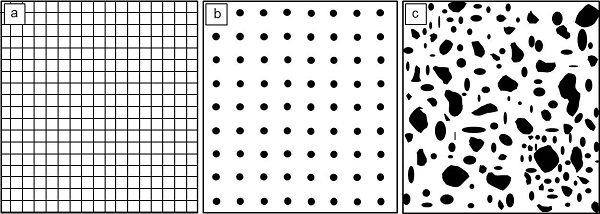
| Bild 1: | Natürliche Oberflächenstruktur von (a): Aluminiumschaum, (b) Polyurethan-Schaum und (c) sandgestrahltem Beton |
Die für die Prüfung erforderlichen Oberflächenmerkmale können natürlicher Art wie z. B. die Rauigkeit oder Poren bei offenzelligen Schäumen oder Luftblasen in Beton sowie Kunstharzen sein (Bild 1), oder diese werden künstlich aufgebracht. Dazu werden auf der Oberfläche regelmäßige Rasterstrukturen, wie z. B. Linien- oder Punktemuster mittels Ätz- oder Siebdruck-Verfahren (Bild 2a und b) aufgebracht oder es werden auf dem zu untersuchenden Oberflächenbereich stochastische Muster generiert (Bild 2c). Je nach Größe des Prüfobjekts können hierzu kommerzielle Spraydosen z. B. für Autolacke (Graphitspray) oder das Paintbrush-Verfahren verwendet werden, wobei die letztere Methode deutlich kleinere Oberflächenmuster erzeugt. Die entstehenden Muster auf der Oberfläche nennt man in Anlehnung an die ESPI- oder Shearographie Methode „Speckles“ oder „Fleckchen“, wobei diese zur Verfolgung der Verschiebungen genutzt werden.
Die regelmäßigen Muster können auch Größenunterschiede und nicht identische Abstände haben oder können bei Linienmustern um einen definierten Winkel geneigt sein. Bei stochastischen Mustern muss eine hinreichende Anzahl von Punkten auf der Oberfläche vorhanden sein, wobei diese nicht zu große Unterschiede aufweisen und sich nicht überlagern sollten, um mittels Mustererkennung eindeutig identifizierbar zu sein.
| Bild 2: | Künstliche Oberflächenraster von (a): Linienmuster, (b) Punktemuster und (c) stochastisches Muster mittels Spray- oder Airbrush-Verfahren |
Messtechnik
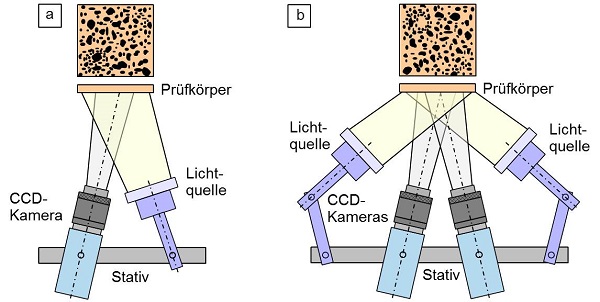
Bevor das präparierte Prüfobjekt oder ein Prüfkörper unter Belastung untersucht werden kann, muss zunächst der optische Aufbau der Messeinrichtung (Bild 3) hinsichtlich Kontrast, Helligkeit und Bildausschnitt und -schärfe optimiert werden. Dazu werden bei einer 3d-Messung die beiden CCD-Kameras bezüglich der optischen Bildachse und der Höhe des Prüfobjekts näherungsweise unter den gleichen Winkel α und β positioniert, so dass die optischen Achsen der Kameras näherungsweise den identischen Bildausschnitt erfassen können (Bild 3b). Falls nur eine der beiden Kameras benutzt wird, ist nur eine 2d-Messung in-plane möglich (Bild 3a). Für die CCD-Kameras stehen im Regelfall mehrere Objektive mit differierender Brennweite und Zwischenringe zur Verfügung, so dass die Entfernung zwischen den oder der Kamera und dem Prüfobjekt an die örtlichen Gegebenheiten individuell anpassbar ist. Die Synchronisation mit externen Signalen (Kraft, Traversenweg) sorgt für eine eindeutige Zuordnung zu den lokalen Deformationsfeldern.
Sind die Bedingungen hinsichtlich Objektschärfe, -helligkeit und Detailerkennbarkeit erfüllt, dann muss der messtechnische Aufbau kalibriert werden, weshalb alle beweglichen Elemente fixiert werden müssen (Bild 3).
| Bild 3: | Schematische Darstellung eines (a): 2d-Messsystems und (b) des 3d-Messsystems |
Da das Objekt-Rasterverfahren neben der Mustererkennung auf der sogenannten Nahbereichsphotogrammetrie beruht, wird die Grauwertverteilung der Objektoberfläche aus zwei differierenden Richtungen bzw. Winkeln registriert und mittels digitaler Bildanalyse (Digital Image Correlation–DIC) berechnet, digitalisiert und die dreidimensionale Geometrie des Verschiebungsfeldes ermittelt [4–7].
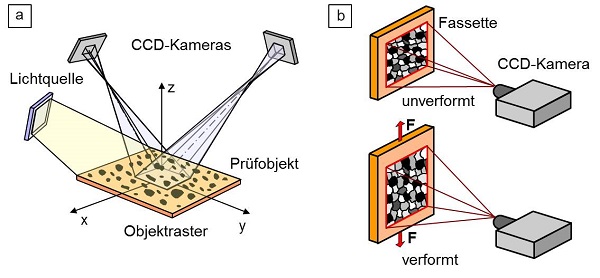
Da einzelne Speckles durch die Mustererkennung schwer verfolgbar oder erkennbar sind, wird eine repräsentative Anzahl von Speckles mit unterschiedlicher Geometrie zu sogenannten Frames oder Fassetten (Bild 4a) zusammengefasst, was natürlich mit der Anzahl der verfügbaren Bildelemente (Pixel) der CCD-Kamera korrespondieren muss. Die Fassette sollte dabei ca. 17 x 17 bis 25 x 25 Pixel in Abhängigkeit von der Pixelzahl der Kamera (z. B. 1024 x 1024 oder 2048 x 2048 Pixel) mit mehreren Speckles umfassen, wobei sich aufeinanderfolgende Fassetten zu ca. 1/3 überlappen sollten, um eine ausreichende Mustererkennung durch die beiden Kameras auch im deformierten Zustand der Speckles zu garantieren (Bild 4b).
| Bild 4: | Schematische Darstellung einer (a): Facette bei 3d-Messung und (b) Erfassung der deformierten Speckles bei einer 2d-Messung |
Durch die Belastung durch Zug, Druck oder Innendruck (siehe: Kriechverhalten Zeitstandinnendruckversuch) können die Flächenelemente auf der Oberfläche in x-, y- und z-Richtungen verschoben oder verzerrt werden oder um die Bezugsachsen rotieren. Durch die intelligente Mustererkennung und Korrelationsverfahren wird dabei sichergestellt, dass die jeweiligen Flächenelemente auch im deformierten Zustand von beiden Kameras erkannt werden. Damit ist dann die Zuordnung des deformierten Objektzustandes zum Ausgangszustand (undeformiert) möglich und der Verschiebungsvektor des betrachteten Bildelements (Punkt bzw. Speckle) kann berechnet werden. Diese Berechnung wird im Rastermode, also der Betrachtung jeweils 1/3 der Fassette, durchgeführt, wodurch dann das Verschiebungsfeld für u, v, w im Bildausschnitt angegeben werden kann. Wird diese Prozedur für alle Speckles der Prüfkörperoberfläche unter Einbeziehung von Subpixelalgorithmen wiederholt, dann ergibt sich nach den Gln. (1) bis (4) das 2d-Dehnungsfeld (in-plane) für εx, εy und die Verzerrung γxy sowie die Rotation ωxy mit hoher Auflösung. Unabhängig davon, ob das 3d- oder 2d-Dehnungsfeld ermittelt wird, entspricht die Berechnung der lokalen Dehnung damit einer Differenzbildung zwischen benachbarten Speckles.
| (1) |
| (2) |
| (3) |
| (4) |
Vor- und Nachteile des Messverfahrens, Anwendungen
Im Vergleich zur Electronic-Speckle-Pattern-Interferometrie (ESPI) ist das Objekt-Rasterverfahren vergleichsweise einfach aufgebaut, billiger und unempfindlich gegenüber externen Schwingungen oder Vibrationen. Desweitern ist speziell die Prüfobjektpräparation bei Nutzung stochastischer Muster relativ einfach, da diese aufgesprüht werden können. Im Allgemeinen besitzt die Laser-Speckle-Interferometrie jedoch gerade bei großen Messobjekten eine wesentlich kleine Messungenauigkeit, allerdings bei kleineren Messflächen ist dieser Wert im Vergleich zum Objekt-Rasterverfahren nur unwesentlich besser. Während die Anwendungen der ESPI auf relativ kleine Verschiebungen (ca. 100 µm) möglich sind, besteht bei dem Objekt-Rasterverfahren keine prinzipielle Begrenzung des Messbereichs. Die zeitliche Auflösung beider Messverfahren wird im Wesentlichen von der Güte der verwendeten CCD-Kameras bestimmt.
Im Ergebnis des Vergleichs zwischen der Laser-Speckle-Interferometrie und dem Objekt-Rasterverfahren, kann man feststellen, dass bei Objektfeldern im Bereich weniger Quadratmillimeter die Vorteile des Objekt-Rasterverfahrens bei der Ermittlung von Dehnungsfeldern überwiegen. Bei größeren Objektfeldern ist die Laser-Speckle-Interferometrie vorteilhaft, insbesondere wenn eine hohe Auflösung und Messgenauigkeit für die Dehnungsanalyse im Vordergrund stehen [8]. Bild 5 zeigt die Anordnung eines derartigen Prüfsystems an einer Universalprüfmaschine Zwick Z020 zum Studium des lokalen Verformungsverhaltens im Zugversuch an Kunststoffen. Dabei wird ein Speckle-Muster auf den Prüfkörper aufgebracht, welches nach Trocknung die lokalen Deformationen auf der Prüfkörperoberfläche widerspiegelt. Lokale makroskopische Inhomogenitäten, wie Schultern des Prüfkörpers oder Spannungskonzentrationen infolge von eingebrachten Löchern (Bild 6) sind an der Veränderung des Dehnungsfeldes genauso detektierbar wie innere herstellungs- oder belastungsbedingte Defekte (Lunker oder Risse).
| Bild 5: | Prüfsystem Q-400 für das Objekt-Rasterverfahren der Fa. LimMess Messtechnik & Software GmbH, Krefeld |
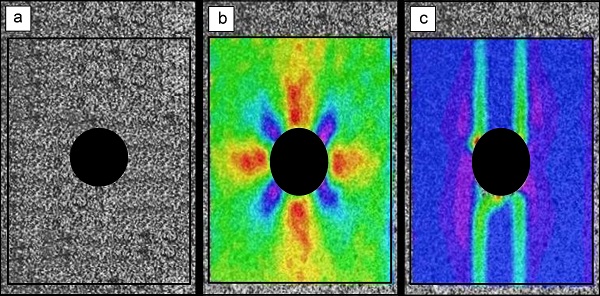
| Bild 6: | Lokale Dehnfelder eines Vielzweckprüfkörpers mit mittigem Bohrloch: (a) Specklemuster, (b) x-Dehnungsfeld kurz vor dem Bruch und (c) Dehnungsverteilung nach dem Bruch des Prüfkörpers |
In Bild 6 sind Bildausschnitte eines Vielzweckprüfkörpers Typ 1A aus Acrylnitril-Butadien-Styrol (Kurzzeichen: ABS) unter Zugbeanspruchung dargestellt, der in der Mitte des Prüfkörpers eine Bohrung mit dem Durchmesser von 3 mm enthält. Das Bild 6a zeigt das aufgesprühte Specklemuster und den Rahmen, der zur Auswertung der Dehnungsverteilung genutzt wurde. In Bild 6b ist die scheinbare Dehnungsverteilung in x-Richtung kurz vor dem Bruch des Prüfkörpers dargestellt, das die lokalen Dehnungen infolge der Spannungskonzentration (siehe: Bruchmechanik) am Loch anschaulich demonstriert. Die lokalen Dehnungen kurz nach dem Bruch des Prüfkörpers sind in Bild 6c zu erkennen und zeigen die Auswirkungen von Spannungskonzentrationen an geometrischen Imperfektionen. Die Software gestattet neben der Auswertung der Ingenieurdehnung (scheinbare Dehnung) auch die Bestimmung der wahren Dehnung sowie der Poissonzahl unter Zugbeanspruchung. Bei Bauteilen aus Kunststoffen oder Kunststoffverbunden ist zudem die Analyse des Deformationszustandes bei statischer, quasistatischer oder dynamischer Beanspruchung als auch der Überlagerung durch thermische und mediale Lasten möglich.
Literaturhinweise
| [1] | Ritter, R.: Feldmeßmethoden zur Ermittlung von Weg- und Dehnungsgrößen-Übersicht über den derzeitigen Stand. In: Tagungsband DVM-Tagung Werkstoffprüfung `93, Bad Nauheim, 2.–3.12. 1993, S. 131−143 (ISSN 0941-5300; siehe AMK-Büchersammlung unter M 49) |
| [2] | Galanulis, K., Ritter, R., Winter, D.: 3D-Verformungsmessung in der Bruchmechanik mit Hilfe des Rasterverfahrens. In: Tagungsband DVM-Tagung Werkstoffprüfung `92, Bad Nauheim, 3.–4.12.1992, S. 167−176 (ISSN 0941-5300; siehe AMK-Büchersammlung unter M 48) |
| [3] | Springmann, M.: Identifikation von Materialparametern schädigungsmechanischer Gesetze unter Einbeziehung der Dehnungslokalisierung. Dissertation Technische Universität Bergakademie Freiberg, 2005 (ISBN 3-89820-926-1) |
| [4] | Tutsch, R., Ritter, R., Petz, M.: Zur flächenhaften zerstörungsfreien Prüfung mit Hilfe optischer Feldmeßtechnik. DGZfP- Jahrestagung Berlin 2001, V24, S. 1–11 |
| [5] | Puente Leon, F., Heizmann, M. (Hrsg.): Forum Bildverarbeitung. KIT Scientific Publishing, Karlsruhe 2010, (ISBN 978-3-86644-578-9) |
| [6] | Blumrich, F.: Optische korrelationsbasierte Messtechnik mittels zufälliger Punktemuster. Dissertation Universität Stuttgart, 2009 |
| [7] | Walter, H., Vogel, D., Michel, B., Grellmann, W.: Bestimmung der Querkontraktionszahl von Polymeren mittels Grauwertkorrelationsanalyse. Tagung Polymerwerkstoffe Halle (Saale), 2002 |
| [8] | Öchsner, A., Winter, W., Kuhn, G.: Verformungs- und Dehnungsfeldermittlung an zellularen Werkstoffen mittels Rasterverfahren. TM – Technisches Messen 66 (1999) 10, S. 386–389 |