Thermische Leitfähigkeit

Ein Service der
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung
PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Thermische Leitfähigkeit von Kunststoffen

Definition

Aus physikalischer Sicht ist prinzipiell zwischen der Wärmeleitfähigkeit, die den Transport von Energie in einem Werkstoff beschreibt und der thermischen Leitfähigkeit oder Temperaturleitfähigkeit zu unterscheiden.

Die Temperaturleitfähigkeit α ist jene Geschwindigkeit, mit der sich Temperaturfelder ${T({\vec {x}})}$ in einem Werkstoff ändern und beschreibt damit die instationäre Wärmeleitung. Sie ist bestimmt durch die Wärmeleitfähigkeit λ, die spezifische Wärmekapazität c_p und durch die Massendichte ρ. Die Temperaturleitfähigkeit ist definiert mit

${\alpha ={\frac {\lambda }{\rho \cdot c_{p}}}}$

(1)

Herleitung

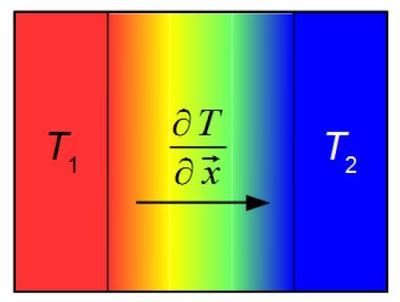
Gegeben seien zwei Behälter mit den Temperaturen T₁ und T₂ und zwischen ihnen ein Übergangsmedium, in dem der Temperaturgradient ≈ ΔT/Δx vorliegt (Bild 1). Der Wärmestrom geht dabei in die Richtung, wie es im Bild durch den Pfeil angedeutet ist. Die Wärmemenge Q₁ mit der Temperatur T₁ fließt im Übergangsmedium zum Behälter mit der Wärmemenge Q₂ der niedrigeren Temperatur T₂. Es findet ein Wärmetransport durch das Übergangsmedium statt. Der Wärmestrom hat die Form

${{\dot {Q}}=m\cdot c_{p}\cdot {\frac {\partial T}{\partial t}}}$.

(2)

Hierbei muss die spezifische Wärmekapazität bei konstantem Druck genommen werden.

Betrachtet man nun die Eigenschaft der Wärmeleitfähigkeit des Übergangsmediums, dann gilt auch (A ist die Wärmedurchtrittsfläche):

${{\dot {Q}}=-\lambda \cdot A\cdot {\frac {\partial T}{\partial x}}}$.

(3)

Bild 1:

Schematische Darstellung des Temperaturgradienten zwischen den Behältern mit den Temperaturen T1 und T2 mit dem Übergangsmedium

Die Gleichsetzung von (2) und (3) liefert noch nicht die Temperaturleitfähigkeit. Dazu muss auf die allgemeine Form dieser Gleichungen zurückgegriffen werden:

Statt des Wärmestroms wird der Wärmestromdichtevektor j betrachtet, also der Wärmestrom durch eine Querschnittsfläche, das 1. Fouriersche Gesetz (4).

${j=-\lambda \cdot grad\ T}$.

(4)

Der Wärmestrom pro Volumen, den der Behälter mit T₁ verliert, ist nach (2)

${{\dot {q}}=\rho \cdot c_{p}\cdot {\frac {\partial T}{\partial t}}}$.

(5)

Gemäß der Kontinuitätsgleichung gilt für den Wärmetransport

${{\frac {\partial q}{\partial t}}=-divj}$.

(6)

Mittels Einsetzen von (4) und (5) in (6) erhält die Kontinuitätsgleichung die Form

${{\frac {\partial T}{\partial t}}={\frac {\lambda }{\rho \cdot c_{p}}}\cdot {\frac {\partial ^{2}T}{\partial x^{2}}}}$.

(7)

womit wieder (1) erhalten wird (2. Fouriersches Gesetz).

Praktische Aspekte

Die Temperaturleitfähigkeit ist eine Eigenschaft des jeweiligen Werkstoffes und ist hier in der Tabelle 1 für eine Auswahl an Kunststoffen aufgelistet. Dieser Kennwert beschreibt den instationären Wärmetransport. So ist es z. B. von Bedeutung, dass die Griffe der die heiße Flüssigkeit enthaltenden Gefäße eine niedrigere Temperaturleitfähigkeit besitzen, um die Verletzungsgefahren mit ihrem Umgang zu reduzieren. Des Weiteren wird diese Größe für die Feuersicherheit von Werkstoffen und die Beurteilung der Wärmespeicherung verwendet.

Tabelle 1: Temperaturleitfähigkeit ausgewählter Kunststoffe

Werkstoff	Temperaturleitfähigkeit α (mm2/s)
PVC-U	0,122
PVC-P	0,145
PE-HD	0,227
PP	0,145
PS	0,115
POM	0,161

Bedeutung

Da die Temperaturleitfähigkeit angibt, mit welcher Geschwindigkeit sich eine Temperatur durch ein Medium ausbreitet, ist sie grundlegend für Untersuchungen zum Wärmetransport in Medien. Dieser Kennwert findet in der Bauindustrie, z. B. für die Wärmedämmung von Gebäuden, Verwendung. Zudem ist die Temperaturleitfähigkeit einfacher und genauer zu messen als die Wärmeleitfähigkeit, weswegen die Wärmeleitfähigkeit häufig indirekt über die Temperaturleitfähigkeit bestimmt wird.

Literaturhinweise

[1]	Landau, L. D., Lifschitz, E. M.: Hydrodynamik – Lehrbuch der theoretischen Physik. Akademie-Verlag, Berlin (1991)
[2]	www.linseis.com: Wärmeleitfähigkeit/Temperaturleitfähigkeit (Zugriff: 24.04.2020)
[3]	Marek, R., Nitsche, K.: Praxis der Wärmeübertragung. Grundlagen – Anwendungen – Übungsaufgaben. 2., aktualisierte und erweiterte Auflage, Fachbuchverlag Leipzig im Carl Hanser Verlag, München (2010) (ISBN 978-3-446-42510-1; siehe AMK-Büchersammlung unter I 43)
[4]	Paus, H.: Physik in Experimenten und Beispielen. Carl Hanser Verlag, München Wien (1995), S. 580 f. (ISBN 3-446-17371-4; siehe AMK-Büchersammlung unter I 4)
[5]	Domininghaus, H., Elsner, P., Eyerer, P., Hirth, T.: Kunststoffe. Eigenschaften und Anwendungen. 8. Auflage, Springer-Verlag, Heidelberg (2012), S. 304 (ISBN 978-3-642-16172-8; siehe AMK-Büchersammlung unter G 41)