Eindruckbruchmechanik
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Eindruckbruchmechanik
Grundlagen der Eindruckbruchmechanik
Die Eindruckbruchmechanik ist ein spezielles Verfahren der linear-elastischen Bruchmechanik, deren Anwendung auf sehr spröde Werkstoffe, meist Keramiken oder Gläser, seltener auch Thermoplaste oder Duromere bzw. Polymer-Keramik-Hybridwerkstoffe, beschränkt ist. Ähnlich wie bei der Härteprüfung dringt während des Belastungsvorganges ein harter Eindringkörper in einen plattenförmigen Prüfkörper ausreichender Dicke und Größe ein. Dabei werden zumeist Vickers- oder Berkovichpyramiden, deutlich seltener auch kegel- oder kugelförmige Eindringkörper verwendet. Die Größe des nach erfolgter Entlastung entstandenen Eindrucks sowie die Länge der während des Belastungsvorganges gewachsenen, auswerterelevanten Risse werden ausgemessen und zusammen mit der maximal aufgebrachten Kraft zur Ermittlung eines Spannungsintensitätsfaktors herangezogen. Die während des Entlastungsvorganges entstandenen Risse erfahren dagegen keinerlei Berücksichtigung. Neben einer spannungsdeterminierten Bewertung des Zähigkeitsverhaltens mittels des Spannungsintensitätsfaktors erfolgt, wenn auch sehr selten, einer energiedeterminierte Bewertung mittels der Energiefreisetzungsrate, was jedoch die Aufnahme von Kraft-Eindringtiefe-Diagrammen im Rahmen der Instrumentierten Härteprüfung voraussetzt.
Grundsätzlich muss zwischen Risssystemen, wie sie z. B. an kugelförmigen Eindringkörpern entstehen, und Risssystemen z. B. an Vickerspyramiden unterschieden werden. Während die Anzahl der auswerterelevanten Risse an kugelförmigen Eindringkörpern unbestimmt ist und auch von der Prüfkraft F abhängig ist, ist die Anzahl der Risse an Vickerspyramiden werkstoffabhängig wohldefiniert.
Rissentstehung an spröden Werkstoffen
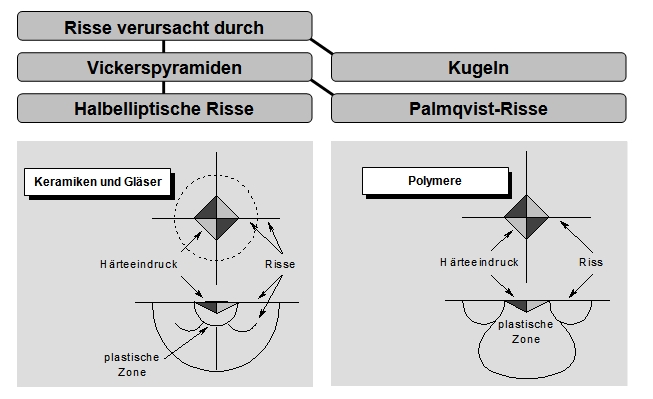
Bei Gläsern und den meisten Keramiken treten zwei, senkrecht aufeinander stehende, halbelliptische Risse auf, während bei polymerbasierten Werkstoffen und einigen Keramiken vier Risse, so genannte Palmqvist-Risse, vorhanden sind, die ihren Ursprung jeweils in den Ecken der Eindrücke haben (siehe Bild 1).
| Bild 1: | Risssentstehung bei Keamiken und Gläsern sowie Polymeren bei Verwendung eines Vickers-Eindringkörpers |
Der Spannungsintensitätsfaktor KI für Kunststoffe
Ausgehend von theoretischen Überlegungen für den Spannungsintensitätsfaktor KI an Vickerspyramiden [1] wurden insgesamt 19 Gleichungen abgeleitet, die entweder für halbelliptische oder Palmqvist-Risse oder beide Risssysteme gültig sind [2, 3]. Für Kunststoffe jedoch hat nur die Methode nach Laugier [4] mit konventionellen bruchmechanischen Verfahren vergleichbare Ergebnisse geliefert [5, 6]:
Hierbei bedeuten:
| m | Verhältnis von Elastizitätsmodul und Härte | |
| a | halbe Länge der Eindruckdiagonalen | |
| c | radiale Risslänge, gemessen vom Zentrum des Eindrucks bis zum Ende des Palmqvist-Risses |
Literaturhinweise
| [1] | Munz, D., Fett, T.: Ceramics – Mechanical Properties, Failure Behaviour, Materials Selection. Springer Series in Materials Science, Vol. 36, Springer Verlag, Berlin (1999) S. 34 ff (ISBN 978-3-642-63580-9, e-Book ISBN 978-3-642-58407-7) |
| [2] | Ponton, C. B., Rawlings, R. D.: Vickers Indentation Fracture Toughness Test, Part 1: Review of Literature and Formulation of Standardised Indentation Toughness Equations. Material Science and Technology 5 (1989) 865–872 |
| [3] | Ponton, C. B., Rawlings, R. D.: Vickers Indentation Fracture Toughness Test, Part 2: Review of Literature and Formulation of Standardised Indentation Toughness Equations. Material Science and Technology 5 (1989) 961–976 |
| [4] | Laugier, M. T.: New Formula for Indentation Toughness in Ceramics. J. Materials Science Letters 8 (1987) 355–356 |
| [5] | Lach, R., Gyurova, L. A., Grellmann, W.: Application of Indentation Fracture Mechanics Approach for Determination of Fracture Toughness of Brittle Polymer Systems. Polymer Testing 26 (2007) 51–59 |
| [6] | Gyurova, L. A.: Application of Indentation Fracture Mechanics Methods for the Investigation of Brittle Polymer Systems. Masterarbeit, Martin-Luther-Universität Halle-Wittenberg, 2005 (siehe AMK-Büchersammlung unter B 3-112) |