J-Integral-Konzept

Ein Service der

Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung
PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

J-Integral-Konzept

Energetische Betrachtung des Bruchvorganges

Das von Cherepanov [1] und Rice [2] eingeführte J-Integral hat auf Grund der energetischen Betrachtung des Bruchvorganges (siehe: Bruch und Brucharten) für Kunststoffe die größte Bedeutung erlangt. Das wegunabhängige Linienintegral umschließt den plastisch deformierten Bereich und verläuft im elastisch deformierten Bereich mit geschlossenem Integrationsweg um die Rissspitze (Bild 1).

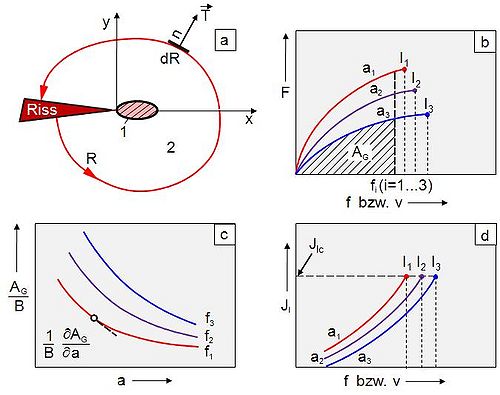
Bild 1:

Bestimmung des J-Integrals: wegunabhängiges Linienintegral mit 1 plastisch deformierter Bereich (energiedissipative Zone) und 2 elastisch deformierter Bereich (a), experimentell ermittelte Kraft-Kraftangriffspunktverschiebungs-Kurven unterschiedlicher Risslänge (b), durch Planimetrieren der F = F(v, f)-Abhängigkeit ermittelte Energie , bezogen auf die Prüfkörperdicke als Funktion der Risslänge (c) und durch Differenzieren der Kurven (c) bestimmtes J-Integral (d) [3]

Die x- und y-Komponenten werden definiert durch

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle J_x\,=\, \int_{R} \left( W \,dy-T_{ij} \cdot n_j \frac{\partial u}{\partial x}dR\right)} und

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle J_y\,=\, \int_{R} \left( -W \,dx-T_{ij} \cdot n_j \frac{\partial u}{\partial x}dR\right)} .

mit

W		elastische Energiedichte
T		Spannungstensor
n		Außennormale der Kurve R um die Rissspitze
u		Verschiebungsvektor

Experimentelle Ermittlung von J-Werten

Die experimentelle Bestimmung erfolgt nach Bild 1 b bis d, indem aus den registrierten Kraft-Kraftangriffspunktverschiebungs-Kurven mit unterschiedlichen Kerbtiefen durch Planimetrieren die Verformungsenergie A_G ermittelt und das Verhältnis A_G/B in Abhängigkeit von a dargestellt wird.

Durch graphische Diffenrentation ergibt sich

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle J\,=\,\frac{1}{B} \frac{\partial A_G}{\partial a}}

als Funktion der Kraftangriffspunktverschiebung bzw. Durchbiegung.

Da der Aufwand zur Bestimmung von J-Werten nach dieser Prozedur für die praktische Kennwertermittlung zu hoch ist, wurden Näherungsformeln entwickelt. Die bekanntesten Verfahren sind:

Korrelationen des J-Integrals zum Spannungsintensitätsfaktor und zur Rissöffnungsverschiebung

Für elastisches Werkstoffverhalten ist das J-Integral mit der Energiefreisetzungsrate G identisch:

	Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle J_{I}\,=\,G_{I}\,=\,{\frac {{K_{I}}^{2}}{E}}}	für ESZ bzw.
	Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle J_I\,=\,G_I\,=\,\frac{{K_I}^2}{E} \left( 1- {\nu}^2 \right)}	für EDZ.

Diese Gleichungen sind für die Umrechnung von J_Ic-Werten in K_Ic^J-Werte anzuwenden.

Der Zusammenhang zwischen J-Integral- und Crack Tip Opening Displacement(CTOD)-Konzept liefert

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle J\,=\,m \cdot \sigma_y \cdot \delta_{Ic}} ,

worin m nach [4, 5] als Constraint-Faktor bezeichnet wird. Die kritischen J-Werte sind geometrieunabhängig, d. h. echte Werkstoffkennwerte, wenn das Kriterium

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle B{,}\ a{,}\ \left( W-a \right)\,\ge\,\varepsilon \frac{J}{\sigma_y}}

mit

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \epsilon \!}

werkstoffabhängige Konstante des Geometriekriteriums des J-Integral-Konzeptes

erfüllt ist.

In [6] werden am Beispiel der Temperaturabhängigkeit der Zähigkeit von unorientierten und durch Kaltwalzen orientierten Polypropylen (Kurzzeichen: PP) der Zusammenhang zwischen den nach dem J-Integral und dem CTOD-Konzept bestimmten bruchmechanischen Kenngrößen betrachtet. Für den Constraint-Faktor (siehe auch: Zähigkeit Temperaturabhängigkeit) wird für den untersuchten PP-Werkstoff m = 0,7 angegeben [7].

Siehe auch

Literaturhinweise

[1]	Cherepanov, G. P.: On Crack Propagation in Continuous Media. Applied Mechanics and Mathematics 31 (1967) 503
[2]	Rice, J. R.: A Path Independent Integral and the Approximate Analysis of Strain Concentration by Notches and Cracks. J. Appl. Mech. (1968) 379–386
[3]	Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024) 4. Auflage, S. 248/249 (ISBN 978-3-446-44718-9; E-Book: ISBN 978-3-446-48105-3; siehe AMK-Büchersammlung unter A 23)
[4]	Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig Stuttgart (1993) 3. Auflage, (ISBN 3-342-00659-5; siehe AMK-Büchersammlung unter E 29-3)
[5]	Anderson, T. L.: Fracture Mechanics. Fundamentals and Applications. 2nd Ed., CRC Press, Boca Raton (1995) 2. Auflage, (ISBN 978-0849342608; siehe AMK-Büchersammlung unter E 8-1), DOI: https://doi.org/10.1201/9781315370293
[6]	Grellmann, W., Che, M.: Assessment of Temperature-dependent Fracture Behaviour with Different Fracture Mechanics Concepts on Example of Unoriented and Cold-rolled Polypropylene. J. Applied Polymer Science 66 (1997) 1237–1249
[7]	Hille, E.: Untersuchungen zum Bruchverhalten des orientierten isotaktischen Polypropylen. Ph.D. Dissertation, Technische Hochschule Leuna-Merseburg (1983)