HERTZ´sche Pressung
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
HERTZ´sche Pressung
Physikalische Grundlagen
Unter der HERTZ´schen Pressung versteht man die größte Spannung, die in der Mitte der Berührungs- oder Kontaktfläche zweier elastischer Körper entsteht.
Die erste grundlegende Arbeit zum Kontaktproblem geht auf Joseph Boussinesq zurück, der das Spannungsfeld für den punktbelasteten elastischen Halbraum berechnete. Wichtigstes Ergebnis seiner Lösung ist, dass die Spannungen im Unendlichen mit 1/r bzw. 1/r2 (r ist der Abstand zum Kontaktpunkt) abklingen. Im Jahr 1881 löste HEINRICH HERTZ das Problem des Kontaktes zwischen zwei elastischen Körpern mit gekrümmten Oberflächen in seiner noch heute maßgeblichen Arbeit "Über die Berührung fester elastischer Körper". Dieses klassische Ergebnis bildet auch heute eine Grundlage der Kontaktmechanik.
Die Beschreibung des elastischen Kontaktes zwischen zwei sich berührenden Körpern erfordert zum einen die genaue Kenntnis der Druckverteilung innerhalb des Kontaktbereiches und zum anderen die sich dadurch ergebenden Oberflächenverschiebungen an jeder Stelle innerhalb und außerhalb der Kontaktfläche. Die erste Annahme der aus diesen Überlegungen resultierenden Theorie ist, dass jeder der am Kontakt beteiligten Körper als ein elastischer Halbraum angesehen wird. Dies bedeutet, dass die Abmessungen des Körpers groß gegenüber den Dimensionen des Kontaktradius sind. Somit sind die Linearitätsbedingungen für den Hookschen Bereich (siehe HOOKE’sches Gesetz) erfüllt und die Randbedingungen der elastischen Kontakttheorie vereinfachen sich:
- die Kontaktspannungen sind auf den Kontaktbereich konzentriert; außerhalb der Kontaktzone fallen die Spannungen exponentiell ab,
- die Kontaktspannungen hängen selbst nicht von der Form der Körper außerhalb der Kontaktzone ab.
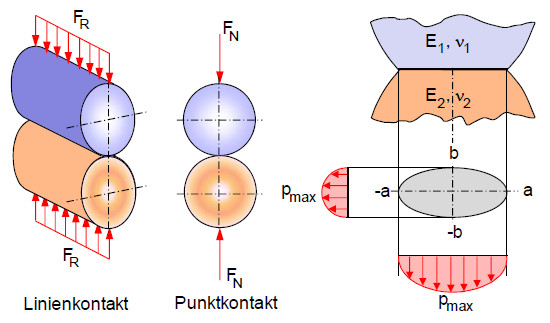
Werden elastische Körper mit gewölbter Oberfläche (Zylinder und/oder Kugeln) gegeneinander oder gegen eine Ebene gepresst, dann berühren sie sich im idealisierten Fall untereinander oder mit der Ebene nur linien- oder punktförmig. Im realen Fall jedoch entsteht bei Annäherung der beiden Körper aneinander oder an eine Ebene, die durch eine von außen angreifende Kraft hervorgerufen wird, an der Berührungsstelle infolge der Abplattung eine ellipsenförmige oder rechteckige Berührungsfläche. Die Größe und Form der Berührungsflächen sowie die Höhe und Verteilung der mechanischen Spannungen (d. h. der Flächenpressungen) unter den Berührungsflächen können berechnet werden. Dabei wird die höchste Spannung, die in der Mitte der Berührungsfläche herrscht, auch HERTZ´sche Pressung genannt. Die Höhe der HERTZ´schen Pressung hängt ab von der Kraft, mit der die beiden Körper aufeinander oder gegen eine Ebene gepresst werden, von den Krümmungsradien und von den Elastizitätsmoduln der beteiligten Körper (Bild 1).
| Bild 1: | Schematische Darstellung der HERTZ´schen Pressung gekrümmter Körper |
Die Voraussetzungen für die Berechnung der Flächenpressung nach den HERTZ´schen Gleichungen sind:
- homogene und isotrope Werkstoffe mit linear-elastischen Materialeigenschaften,
- eine ebene Kontaktfläche, die klein gegenüber den geometrischen Abmessungen der Körper ist,
- infolge Reibungsfreiheit treten keine Schubspannungen in der Kontaktfläche auf,
- Betrachtung der beiden Körper als elastische Halbräume.
Die HERTZ´sche Pressung pmax bei Kontakt gekrümmter Oberflächen berechnet sich dabei allgemein nach folgender Gleichung:
mit:
| F | Kraft FN oder FR zwischen den Körpern, | |
| E/(1-ν2) | reduzierter Elastizitätsmodul | |
| ξ,η | Beiwerte nach Hertz für die Berührung gekrümmter Oberflächen und | |
| K | Krümmung |
Für den reduzierten Modul gilt:
mit:
| ν1,ν2 | Poissonzahl (Querkontraktionszahl) der Körper 1 und 2 sowie | |
| E1, E2 | E-Modul der Körper 1 und 2. |
Punktberührung Kugel – Kugel
Für den einfachen Berührungsfall zweier identischer Kugeln oder einer Kugel mit einer Ebene gilt (identische Materialien):
mit n = 6 (Kugel – Kugel) bzw. n = 1,5 (Kugel – Ebene)
wobei R der Kugelradius und ν die Poissonzahl ist.
Linienberührung (Zylinder – Zylinder und Zylinder – Ebene)
Für den einfachen Berührungsfall zweier identischer Zylinder oder eines Zylinders mit einer Ebene gilt (identische Materialien):
mit n = 1 (Zylinder – Zylinder) bzw. n = 0,5 (Zylinder – Ebene)
wobei R der Zylinderradius und l die Berührungslänge der Zylinder (bzw. des Zylinders mit der Ebene) ist.
Bei Überschreiten der Elastizitätsgrenze, d. h. der durch den Werkstoff maximal ertragbaren HERTZ´schen Pressung, kommt es in sehr duktilen Werkstoffen zum seitlichen Ausweichung des Materials (plastische Deformation) verbunden mit einer dauerndern Kompression. In spröderen Werkstoffen können außerdem auch oder ausschließlich Materialausbrüche und Rissbildung beobachtet werden.
Literaturhinweis
- Hertz, H.: Über die Berührung fester elastischer Körper. Jounal für die reine und angewandte Mathematik 92 (1881) S. 56–171
- Hertz, H.: Über die Brührung fester elastischer Körper und über die Härte. Verhandlungen des Vereins zur Beförderung des Gewerbefleißes. 61 (1982), S. 449–463
- Geike, T.: Theoretische Grundlagen eines schnellen Berechnungsverfahrens für den Kontakt rauer Oberflächen. Dissertation. Technische Universität Berlin, Berlin (2008), S. 15
- Enders; S.: Untersuchungen der mechanischen Eigenschaften von spröden Schicht- und Kompaktsystemen durch Deformation kleiner Volumina. Dissertation. Martin-Luther-Universität Halle-Wittenberg, Halle (2000), S. 4–6
- Popov, V. L.: Kontaktmechanik und Reibung. Ein Lehr und Anwendungsbuch von der Nanotribologie bis zur numerischen Simulation. Springer Verlag, Berlin Heidelberg (2009), S. 61–68
- Kunz, J., Jakober, D., Studer, M.: Kontaktmechanik: Längeneinfluss auf die Abspaltung paralleler Zylinder. Contact Mechanics: Influence of the Length of Parallel Cylinders on the Flattening. Konstruktion 6 (2017) S. 63–67
![{\displaystyle p_{max}\,=\,{\frac {1}{\xi \cdot \eta }}\cdot {\frac {1}{\pi }}\cdot {\sqrt[{3}]{\frac {1,5F\cdot E^{2}\cdot \left(\sum k\right)^{2}}{\left(1-\nu ^{2}\right)^{2}}}}}](https://de.wikipedia.org/api/rest_v1/media/math/render/svg/4f4de9f2f649b0c71d713efbbb9487715646c699)

![{\displaystyle p_{max}\,=\,{\frac {1}{\pi }}\cdot {\sqrt[{3}]{\frac {nF\cdot E^{2}}{R^{2}\left(1-\nu ^{2}\right)^{2}}}}}](https://de.wikipedia.org/api/rest_v1/media/math/render/svg/b51d6eece3285773879e39b0a9ace41a1b6650e6)
