Erweitertes CTOD-Konzept: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „{{PSM_Infobox}} <span style="font-size:1.2em;font-weight:bold;">Erweitertes CTOD-Konzept</span> __FORCETOC__ ==Die kritische Rissöffnungsverschiebung δ== …“ |
Keine Bearbeitungszusammenfassung |
||
| (3 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 18: | Zeile 18: | ||
|n | |n | ||
|width="15px" | | |width="15px" | | ||
|Rotationsfaktor | |[[Plastic-Hinge-Modell#Der_Rotationsfaktor_n|Rotationsfaktor]] | ||
|- | |- | ||
|W | |W | ||
| Zeile 37: | Zeile 37: | ||
|} | |} | ||
Die Rissöffnungsverschiebung δ ist immer dann vorteilhaft einsetzbar, wenn Werkstoffanwender oder -entwickler eine Kenngröße suchen, welche die zunehmende Versprödung deutlich beschreibt und eine geometrieunabhängige Größe (siehe: [[Geometriekriterium|Geometriekriterien]]) darstellt. | |||
==Die Aufsplittung der Durchbiegung== | ==Die Aufsplittung der Durchbiegung== | ||
| Zeile 80: | Zeile 80: | ||
Die bruchmechanischen Kenngrößen δ<sub>Id</sub> (berechnet mit f<sub>max</sub>), δ<sub>Id<sub>K</sub></sub> (berechnet mit dem Kerbanteil f<sub>K</sub>) und δ<sub>Id<sub>B</sub></sub> (berechnet mit dem Biegeanteil f<sub>B</sub>) zeigen einen analogen qualitativen Kurvenverlauf wie die in '''Bild 1''' und '''Bild 2''' gewählten Darstellungen. | Die bruchmechanischen Kenngrößen δ<sub>Id</sub> (berechnet mit f<sub>max</sub>), δ<sub>Id<sub>K</sub></sub> (berechnet mit dem Kerbanteil f<sub>K</sub>) und δ<sub>Id<sub>B</sub></sub> (berechnet mit dem Biegeanteil f<sub>B</sub>) zeigen einen analogen qualitativen Kurvenverlauf wie die in '''Bild 1''' und '''Bild 2''' gewählten Darstellungen. | ||
==Siehe auch== | |||
*[[Crack Tip Opening Displacement-Konzept]] | |||
*[[Bruchmechanik]] | |||
*[[Rissöffnung]] | |||
*[[Plastic-Hinge-Modell]] | |||
*[[IKBV Nichtlineares Werkstoffverhalten]] | |||
| Zeile 89: | Zeile 96: | ||
|-valign="top" | |-valign="top" | ||
|[2] | |[2] | ||
|Grellmann, W.: Beurteilung der Zähigkeitseigenschaften von Polymerwerkstoffen durch bruchmechanische Kennwerte. Habilitation (1986), Technische Hochschule Merseburg, Wiss. Zeitschrift TH Merseburg 28 (1986) H. 6, S. 787‒788 ([ | |[[Grellmann,_Wolfgang|Grellmann, W.]]: Beurteilung der Zähigkeitseigenschaften von Polymerwerkstoffen durch bruchmechanische Kennwerte. Habilitation (1986), [https://de.wikipedia.org/wiki/Technische_Hochschule_Leuna-Merseburg Technische Hochschule Leuna-Merseburg], Wiss. Zeitschrift TH Merseburg 28 (1986) H. 6, S. 787‒788 ([https://www.polymerservice-merseburg.de/fileadmin/inhalte/psm/veroeffentlichungen/Habil_Grellmann_Inhaltsverzeichnis.pdf Inhaltsverzeichnis], [https://www.polymerservice-merseburg.de/fileadmin/inhalte/psm/veroeffentlichungen/Habil_Grellmann_Kurzfassung.pdf Kurzfassung]) | ||
|} | |} | ||
[[Kategorie:Bruchmechanik]] | [[Kategorie:Bruchmechanik]] | ||
[[Kategorie:Instrumentierter Kerbschlagbiegeversuch]] | |||
Aktuelle Version vom 8. Oktober 2024, 10:20 Uhr
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Erweitertes CTOD-Konzept
Die kritische Rissöffnungsverschiebung δ
Die nach dem Crack Opening Displacement (CTOD-Konzept) ermittelte bruchmechanische Kenngröße Rissöffnungsverschiebung δ (siehe Rissöffnung) ist geeignet, um die Verformungsfähigkeit der Werkstoffe zu beschreiben. Für den Fall eines Dreipunktbiegeprüfkörpers ergibt sich als Bestimmungsgleichung (1) für δ:
| (1) |
mit
| n | Rotationsfaktor | |
| W | Prüfkörperbreite | |
| a | Kerbtiefe (Risslänge) | |
| fmax | maximale Durchbiegung | |
| s | Stützweite (siehe Auflagerabstand) |
Die Rissöffnungsverschiebung δ ist immer dann vorteilhaft einsetzbar, wenn Werkstoffanwender oder -entwickler eine Kenngröße suchen, welche die zunehmende Versprödung deutlich beschreibt und eine geometrieunabhängige Größe (siehe: Geometriekriterien) darstellt.
Die Aufsplittung der Durchbiegung
Unter der Annahme [1], dass sich die experimentell gemessene Prüfkörperdurchbiegung fmax aus dem durch die Biegung des ungekerbten Teils fB und dem durch die Deformation im Bereich des Kerbes hervorgerufenen Anteil fK (Kerbanteil) nach Gl. (2)
| (2) |
zusammensetzt, wobei der Biegeanteil fB über die Gl. (3)
| (3) |
mit E = Elastizitätsmodul errechnet wird, kann der Zusammenhang zwischen Durchbiegung und dem a/W-Verhältnis gedeutet werden. Bei der Verwendung der kritischen Rissöffnung δ besteht somit die Möglichkeit den Einfluss der reinen Biegung in Form des Durchbiegungsanteils und den Kerbanteil zu separieren.
Anwendung des erweiterten CTOD-Konzeptes für Polypropylen (PP), Polyamid (PA) und chloriertes Polyvinylchlorid (PVCC)
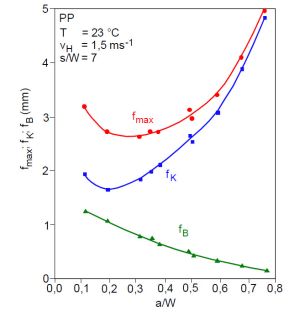
Man erkennt aus dem Bild 1, dass der Biegeanteil mit zunehmendem a/W-Verhältnis abfällt, d. h. bei a/W = 0,1 hat er einen Anteil von 40 % an der Gesamtdurchbiegung und bei a/W = 0,7 nur noch von 5 %. Für hohe Kerbtiefen dominiert der Anteil fK [2].
| Bild 1: | Durchbiegungsanteile fmax, fK und fB bei Beginn der instabilen Rissausbreitung für PP [2] |
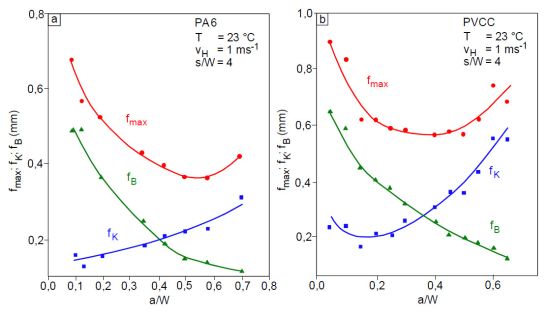
| Bild 2: | Durchbiegungsanteile fmax, fK und fB bei Beginn der instabilen Rissausbreitung für Polyamid 6 und PVCC [2] |
Die bruchmechanischen Kenngrößen δId (berechnet mit fmax), δIdK (berechnet mit dem Kerbanteil fK) und δIdB (berechnet mit dem Biegeanteil fB) zeigen einen analogen qualitativen Kurvenverlauf wie die in Bild 1 und Bild 2 gewählten Darstellungen.
Siehe auch
- Crack Tip Opening Displacement-Konzept
- Bruchmechanik
- Rissöffnung
- Plastic-Hinge-Modell
- IKBV Nichtlineares Werkstoffverhalten
Literaturhinweise
| [1] | Srawley, J. E.: Wide Range Stress Intensity Factor Expressions for ASTM E 399 Standard Fracture Toughness Specimens. International J. of Fracture Mechan. 12 (1976) 475–476 |
| [2] | Grellmann, W.: Beurteilung der Zähigkeitseigenschaften von Polymerwerkstoffen durch bruchmechanische Kennwerte. Habilitation (1986), Technische Hochschule Leuna-Merseburg, Wiss. Zeitschrift TH Merseburg 28 (1986) H. 6, S. 787‒788 (Inhaltsverzeichnis, Kurzfassung) |