Ebener Spannungszustand: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „{{PSM_Infobox}} <span style="font-size:1.2em;font-weight:bold;">Ebener Spannungs- und Dehnungszustand</span> __FORCETOC__ ==Verallgemeinerndes HOOKE'sches Gesetz=…“ |
Keine Bearbeitungszusammenfassung |
||
| (2 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 13: | Zeile 13: | ||
|} | |} | ||
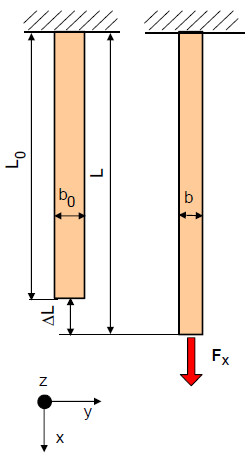
Dabei ist zu erkennen, dass die Dehnung in der jeweiligen Achsenrichtung primär durch die Spannung in der gleichen Achse hervorgerufen wird, aber ein zusätzlicher Dehnungsanteil aus den anderen Spannungsrichtungen, abhängig von der [[Querkontraktion|Poissonzahl]] ν und dem [[Elastizitätsmodul|E-Modul E]], hinzukommt. Bei einer einachsigen Beanspruchung im [[Zugversuch|Zug]]- oder [[Druckversuch]] entsteht neben der Längsdehnung ε<sub>x</sub> eine Querdehnung ε<sub>y</sub> und ε<sub>z</sub>, d. h. in der Breiten- und Dickenrichtung des [[Prüfkörper]]s, falls ein ebener Spannungszustand (ESZ) vorliegt. Das ist in der Regel dann erfüllt, wenn ein hinreichend schlanker [[Prüfkörper]] verwendet wird, der die Messung der Querdehnung in der Breiten- oder Dickenrichtung erlaubt ('''Bild 1'''). | Dabei ist zu erkennen, dass die Dehnung in der jeweiligen Achsenrichtung primär durch die Spannung in der gleichen Achse hervorgerufen wird, aber ein zusätzlicher Dehnungsanteil aus den anderen Spannungsrichtungen, abhängig von der [[Querkontraktion|Poissonzahl]] ν und dem [[Elastizitätsmodul|E-Modul E]], hinzukommt. Bei einer [[Einachsiger Spannungszustand|einachsigen]] Beanspruchung im [[Zugversuch|Zug]]- oder [[Druckversuch]] entsteht neben der Längsdehnung ε<sub>x</sub> eine Querdehnung ε<sub>y</sub> und ε<sub>z</sub>, d. h. in der Breiten- und Dickenrichtung des [[Prüfkörper]]s, falls ein ebener Spannungszustand (ESZ) vorliegt. Das ist in der Regel dann erfüllt, wenn ein hinreichend schlanker [[Prüfkörper]] verwendet wird, der die Messung der Querdehnung in der Breiten- oder Dickenrichtung erlaubt ('''Bild 1'''). | ||
[[Datei:edz1.jpg]] | [[Datei:edz1.jpg]] | ||
| Zeile 76: | Zeile 76: | ||
|} | |} | ||
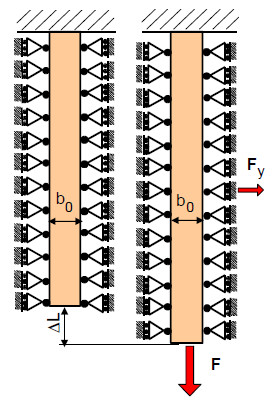
Die entstehende Längsdehnung ε<sub>x</sub> soll identisch sein, weshalb aufgrund des größeren Querschnitts A<sub>0</sub> eine erhöhte Normalspannung σ<sub>x</sub> erforderlich ist. Zur Erklärung dieses Sachverhaltes kann man eine identische Geometrie wie in '''Bild 1''' annehmen, wobei allerdings eine mögliche Breitenänderung des [[Prüfkörper]]s durch seitliche Widerlager verhindert wird ('''Bild 3'''). Könnte man diese Widerlager zusätzlich mit einer Vielzahl von [[Elektro-Mechanischer Kraftaufnehmer | Die entstehende Längsdehnung ε<sub>x</sub> soll identisch sein, weshalb aufgrund des größeren Querschnitts A<sub>0</sub> eine erhöhte Normalspannung σ<sub>x</sub> erforderlich ist. Zur Erklärung dieses Sachverhaltes kann man eine identische Geometrie wie in '''Bild 1''' annehmen, wobei allerdings eine mögliche Breitenänderung des [[Prüfkörper]]s durch seitliche Widerlager verhindert wird ('''Bild 3'''). Könnte man diese Widerlager zusätzlich mit einer Vielzahl von Kraftmessdosen (siehe: [[Elektro-Mechanischer Kraftaufnehmer]] und [[Piezoelektrischer Kraftaufnehmer]]) ausstatten, dann wären die Kräfte in der Breiten- und Dickenrichtung des Prüfkörpers messtechnisch erfassbar. Bei Belastung würde dann eine identische Längsdehnung ε<sub>x</sub> entsprechend Gl. (3) und eine höhere Normalspannung σ<sub>x</sub> entstehen. Eine Poissonzahl ν kann in diesem Fall nicht mehr berechnet werden, da die Dehnungen ε<sub>y</sub> und ε<sub>z</sub> gleich Null sind. Da in diesem simulierten Zustand Kräfte in y- und z-Richtung gemessen würden, entstehen somit auch Spannungen in diese Richtungen deren Betrag sich nach Gl. (1) berechnen lässt [1]. | ||
[[Datei:edz3.jpg]] | [[Datei:edz3.jpg]] | ||
| Zeile 84: | Zeile 84: | ||
|width="600px" |Simulation des schlanken Prüfkörpers im ebenen Dehnungszustand | |width="600px" |Simulation des schlanken Prüfkörpers im ebenen Dehnungszustand | ||
|} | |} | ||
==Siehe auch== | |||
*[[Einachsiger Spannungszustand]] | |||
*[[Energieelastizität]] | |||
*[[Rissmodell nach IRWIN und Mc CLINTOCK]] | |||
*[[Plastische Zone]] | |||
*[[Plastic-Hinge-Modell]] | |||
| Zeile 90: | Zeile 97: | ||
|-valign="top" | |-valign="top" | ||
|[1] | |[1] | ||
|Bierögel, C.: Quasistatische Prüfverfahren. In: Grellmann, W., [[Seidler,_Sabine|Seidler, S.]] (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München ( | |[[Bierögel,_Christian|Bierögel, C.]]: Quasistatische Prüfverfahren. In: [[Grellmann,_Wolfgang|Grellmann, W.]], [[Seidler,_Sabine|Seidler, S.]] (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024) 4. Auflage, S. 106–140 (ISBN 978-3-446-44718-9; E-Book: ISBN 978-3-446-48105-3; siehe [[AMK-Büchersammlung]] unter A 23) | ||
|} | |} | ||
[[Kategorie:Bruchmechanik]] | [[Kategorie:Bruchmechanik]] | ||
[[Kategorie:Deformation]] | [[Kategorie:Deformation]] | ||
Aktuelle Version vom 8. Oktober 2024, 08:47 Uhr
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Ebener Spannungs- und Dehnungszustand
Verallgemeinerndes HOOKE'sches Gesetz
Bei Annahme von isotropen Werkstoffeigenschaften in allen Raum- bzw. Achsenrichtungen ergibt sich das verallgemeinerte HOOKE’sche Gesetz (Gl.1) wie folgt:
| (1) |
Dabei ist zu erkennen, dass die Dehnung in der jeweiligen Achsenrichtung primär durch die Spannung in der gleichen Achse hervorgerufen wird, aber ein zusätzlicher Dehnungsanteil aus den anderen Spannungsrichtungen, abhängig von der Poissonzahl ν und dem E-Modul E, hinzukommt. Bei einer einachsigen Beanspruchung im Zug- oder Druckversuch entsteht neben der Längsdehnung εx eine Querdehnung εy und εz, d. h. in der Breiten- und Dickenrichtung des Prüfkörpers, falls ein ebener Spannungszustand (ESZ) vorliegt. Das ist in der Regel dann erfüllt, wenn ein hinreichend schlanker Prüfkörper verwendet wird, der die Messung der Querdehnung in der Breiten- oder Dickenrichtung erlaubt (Bild 1).
| Bild 1: | Deformation des Prüfkörpers unter Belastung im ebenen Spannungszustand |
Neben der Normalspannung σx (Gl. 2) entsteht bei der Belastung eine Längsdehnung εx oder εL (Gl. 3) sowie eine Querdehnung in der Breiten- und Dickenrichtung (Gl. 4).
| (2) |
| (3) |
| (4) |
Bei Isotropie und homogenem Werkstoffzustand ist die Dehnung in Breitenrichtung εy und in Dickenrichtung εz (Gl. 5) identisch, wobei für beide Querdehnungen jeweils der Absolutbetrag angegeben wird. Die Spannungen σy und σz sind im ebenen Spannungszustand gleich Null.
| (5) |
Ermittlung der Poissonzahl
Die Poissonzahl oder auch Querkontraktionszahl berechnet sich dann nach Gl. (6):
| (6) |
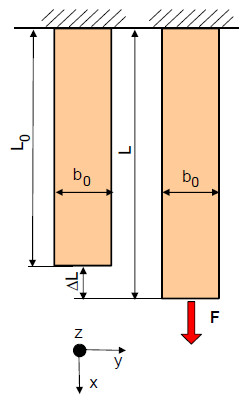
Verwendet man statt des schlanken Prüfkörpers einen dickeren und/oder breiteren prismatischen Prüfkörper entsprechend Bild 2, dann wird sowohl in Dicken- als auch Breitenrichtung kein messbares Dehnungssignal erhalten, da sich der Prüfkörper jetzt im ebenen Dehnungszustand (EDZ) befindet.
| Bild 2: | Deformation des Prüfkörpers unter Belastung im ebenen Dehnungszustand |
Die entstehende Längsdehnung εx soll identisch sein, weshalb aufgrund des größeren Querschnitts A0 eine erhöhte Normalspannung σx erforderlich ist. Zur Erklärung dieses Sachverhaltes kann man eine identische Geometrie wie in Bild 1 annehmen, wobei allerdings eine mögliche Breitenänderung des Prüfkörpers durch seitliche Widerlager verhindert wird (Bild 3). Könnte man diese Widerlager zusätzlich mit einer Vielzahl von Kraftmessdosen (siehe: Elektro-Mechanischer Kraftaufnehmer und Piezoelektrischer Kraftaufnehmer) ausstatten, dann wären die Kräfte in der Breiten- und Dickenrichtung des Prüfkörpers messtechnisch erfassbar. Bei Belastung würde dann eine identische Längsdehnung εx entsprechend Gl. (3) und eine höhere Normalspannung σx entstehen. Eine Poissonzahl ν kann in diesem Fall nicht mehr berechnet werden, da die Dehnungen εy und εz gleich Null sind. Da in diesem simulierten Zustand Kräfte in y- und z-Richtung gemessen würden, entstehen somit auch Spannungen in diese Richtungen deren Betrag sich nach Gl. (1) berechnen lässt [1].
| Bild 3: | Simulation des schlanken Prüfkörpers im ebenen Dehnungszustand |
Siehe auch
- Einachsiger Spannungszustand
- Energieelastizität
- Rissmodell nach IRWIN und Mc CLINTOCK
- Plastische Zone
- Plastic-Hinge-Modell
Literaturhinweis
| [1] | Bierögel, C.: Quasistatische Prüfverfahren. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024) 4. Auflage, S. 106–140 (ISBN 978-3-446-44718-9; E-Book: ISBN 978-3-446-48105-3; siehe AMK-Büchersammlung unter A 23) |