Geometriekriterium: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (3 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Language_sel|LANG=eng|ARTIKEL=Geometry Criterion}} | |||
{{PSM_Infobox}} | {{PSM_Infobox}} | ||
<span style="font-size:1.2em;font-weight:bold;">Geometriekriterium</span> | <span style="font-size:1.2em;font-weight:bold;">Geometriekriterium</span> | ||
| Zeile 21: | Zeile 22: | ||
Die Geometriekonstante <math>\beta</math> ist werkstoffabhängig. | Die Geometriekonstante <math>\beta</math> ist werkstoffabhängig. | ||
Experimentelle Ergebnisse bezüglich des Einflusses der Prüfkörperdicke B auf die bruchmechanischen Kennwerte (siehe [[Bruchmechanische Prüfung]]) für [[Kunststoffe]] liegen in der Literatur vor. In '''Bild 1''' wird die Abhängigkeit des Koeffizienten <math>\beta</math> nach obiger Gleichung von der bei [[quasistatische Prüfverfahren|quasistatischer]] und schlagartiger Beanspruchung (siehe: [[Schlagbeanspruchung Kunststoffe]]) bestimmten [[Bruchmechanik|Bruchzähigkeit]] für verschiedene Kunststoffe gezeigt. Der dargestellte Zusammenhang wurde auf der Grundlage experimentell ermittelter Dicken- und a/W-Abhängigkeiten erstellt und besitzt einen hohen Verallgemeinerungsgrad, da sich unabhängig von der [[Beanspruchung|Beanspruchungsart]] (quasistatisch, schlagartig) und dem Werkstoffversagen (stabil, instabil) ein gemeinsamer Zusammenhang ergibt. | Experimentelle Ergebnisse bezüglich des Einflusses der Prüfkörperdicke B auf die bruchmechanischen Kennwerte (siehe [[Bruchmechanische Prüfung]]) für [[Kunststoffe]] liegen in der Literatur vor. In '''Bild 1''' wird die Abhängigkeit des Koeffizienten <math>\beta</math> nach obiger Gleichung von der bei [[quasistatische Prüfverfahren|quasistatischer]] und schlagartiger Beanspruchung (siehe: [[Schlagbeanspruchung Kunststoffe]]) bestimmten [[Bruchmechanik|Bruchzähigkeit]] für verschiedene Kunststoffe gezeigt. Der dargestellte Zusammenhang wurde auf der Grundlage experimentell ermittelter Dicken- und a/W-Abhängigkeiten erstellt und besitzt einen hohen Verallgemeinerungsgrad, da sich unabhängig von der [[Beanspruchung|Beanspruchungsart]] (quasistatisch, schlagartig) und dem Werkstoffversagen (stabil, instabil) ein gemeinsamer Zusammenhang ergibt (siehe: [[Rissausbreitung]]). | ||
[[Datei:Bild-Geometrie-K-Lexikon.jpg|400px]] | [[Datei:Bild-Geometrie-K-Lexikon.jpg|400px]] | ||
| Zeile 34: | Zeile 35: | ||
* [[Blumenauer, Horst|Blumenauer, H.]], Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig Stuttgart (1993) (ISBN 3-342-00659-5; siehe [[AMK-Büchersammlung]] unter E 29-3) | * [[Blumenauer, Horst|Blumenauer, H.]], Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig Stuttgart (1993) (ISBN 3-342-00659-5; siehe [[AMK-Büchersammlung]] unter E 29-3) | ||
* Anderson, T. L.: Fracture Mechanics. Fundamentals and Applications. 3rd Ed., CRC Press, Boca Raton (2005) (ISBN 978-0849342608; siehe [[AMK-Büchersammlung]] unter E 8-2)) | * Anderson, T. L.: Fracture Mechanics. Fundamentals and Applications. 3rd Ed., CRC Press, Boca Raton (2005) (ISBN 978-0849342608; siehe [[AMK-Büchersammlung]] unter E 8-2)), DOI: [https://doi.org/10.1201/9781315370293 https://doi.org/10.1201/9781315370293] | ||
* Grellmann, W., [[Seidler,_Sabine|Seidler, S.]], Lach, R.: Geometrieunabhängige bruchmechanische Werkstoffkenngrößen – Voraussetzung für die Zähigkeitscharakterisierung von Kunststoffen. Materialwissenschaften und Werkstofftechnik 32 (2001) 552–561 | * [[Grellmann,_Wolfgang|Grellmann, W.]], [[Seidler,_Sabine|Seidler, S.]], [https://researchgate.net/profile/Ralf-Lach Lach, R.]: Geometrieunabhängige bruchmechanische Werkstoffkenngrößen – Voraussetzung für die Zähigkeitscharakterisierung von Kunststoffen. Materialwissenschaften und Werkstofftechnik 32 (2001) 552–561 | ||
* Akay, M.: Fracture Mechanics Properties. In: Brown, R. P. (Ed.): Handbook of Polymer Testing. Marcel Dekker Inc., New York (1999) 533–588 (ISBN 978-0824701710; siehe [[AMK-Büchersammlung]] unter C 5) | * Akay, M.: Fracture Mechanics Properties. In: Brown, R. P. (Ed.): Handbook of Polymer Testing. Marcel Dekker Inc., New York (1999) 533–588 (ISBN 978-0824701710; siehe [[AMK-Büchersammlung]] unter C 5) | ||
* Williams, J. G.: Fracture Mechanics of Polymers. Ellis Horwood Ltd., Publisher (1984) (ISBN 978-0470-20013-1; siehe [[AMK-Büchersammlung]] unter E 42) | |||
== Geometriekriterium, J-Integral-Konzept == | == Geometriekriterium, J-Integral-Konzept == | ||
| Zeile 72: | Zeile 74: | ||
'''Literaturhinweise''' | '''Literaturhinweise''' | ||
* Grellmann, W., [[Seidler,_Sabine|Seidler, S.]], Lach, R.: Geometrieunabhängige bruchmechanische Werkstoffkenngrößen – Voraussetzung für die Zähigkeitscharakterisierung von Kunststoffen. Materialwissenschaften und Werkstofftechnik 32 (2001) 552–561 | * [[Grellmann,_Wolfgang|Grellmann, W.]], [[Seidler,_Sabine|Seidler, S.]], [https://researchgate.net/profile/Ralf-Lach Lach, R.]: Geometrieunabhängige bruchmechanische Werkstoffkenngrößen – Voraussetzung für die Zähigkeitscharakterisierung von Kunststoffen. Materialwissenschaften und Werkstofftechnik 32 (2001) 552–561 | ||
* Grellmann, W.: Neue Entwicklungstendenzen bei der bruchmechanischen Zähigkeitscharakterisierung von Kunststoffen und Verbunden. In: Grellmann, W., [[Seidler,_Sabine|Seidler, S.]]: Deformation und Bruchverhalten von Kunststoffen. Springer Verlag, Berlin Heidelberg (1998) S. 3–26, (ISBN 3-540-63671-4; e-Book (2014): ISBN 978-3-642-58766-5; siehe [[AMK-Büchersammlung]] unter A 6) | * [https://www.researchgate.net/profile/Wolfgang-Grellmann Grellmann, W.]: Neue Entwicklungstendenzen bei der bruchmechanischen Zähigkeitscharakterisierung von Kunststoffen und Verbunden. In: Grellmann, W., [[Seidler,_Sabine|Seidler, S.]]: Deformation und Bruchverhalten von Kunststoffen. Springer Verlag, Berlin Heidelberg (1998) S. 3–26, (ISBN 3-540-63671-4; e-Book (2014): ISBN 978-3-642-58766-5; siehe [[AMK-Büchersammlung]] unter A 6) | ||
== Geometriekriterium, Rissöffnungsverschiebung == | == Geometriekriterium, Rissöffnungsverschiebung == | ||
| Zeile 99: | Zeile 101: | ||
|} | |} | ||
Neben dem [[J-Integral-Konzept]] wird insbesondere zur Beschreibung verformungsdeterminierter Bruchvorgänge das [[Crack Tip Opening Displacement-Konzept|CTOD-Konzept]] verwendet. Voraussetzung für die Ermittlung kritischer Rissöffnungen ist die Ausbildung eines quasistatischen Spannungszustandes. Auf der Basis des [[Plastic-Hinge Modell|Plastic-Hinge-Modells]] wird bei schlagartiger Beanspruchung die kritische [[Rissöffnung]] ermittelt, die bei B = 4 mm für a/W > 0,2 unabhängig vom a/W-Verhältnis ist. Aus '''Bild 3''' wird ersichtlich, dass man <math>\xi</math>-Werte zwischen 10 und 90 annehmen kann und bei noch unbekannter Abschätzung der notwendigen Kerbtiefe bzw. Prüfkörperdicke eine erhebliche Überschätzung der erforderlichen Mindestprüfkörperabmessungen möglich ist. | Neben dem [[J-Integral-Konzept]] wird insbesondere zur Beschreibung verformungsdeterminierter Bruchvorgänge das [[Crack Tip Opening Displacement-Konzept|CTOD-Konzept]] verwendet. Voraussetzung für die Ermittlung kritischer Rissöffnungen ist die Ausbildung eines quasistatischen Spannungszustandes. Auf der Basis des [[Plastic-Hinge-Modell|Plastic-Hinge-Modells]] wird bei schlagartiger Beanspruchung die kritische [[Rissöffnung]] ermittelt, die bei B = 4 mm für a/W > 0,2 unabhängig vom a/W-Verhältnis ist. Aus '''Bild 3''' wird ersichtlich, dass man <math>\xi</math>-Werte zwischen 10 und 90 annehmen kann und bei noch unbekannter Abschätzung der notwendigen Kerbtiefe bzw. Prüfkörperdicke eine erhebliche Überschätzung der erforderlichen Mindestprüfkörperabmessungen möglich ist. | ||
==Siehe auch== | |||
*[[Bruchsicherheitskriterium]] | |||
'''Literaturhinweise''' | '''Literaturhinweise''' | ||
* Grellmann, W., [[Seidler,_Sabine|Seidler, S.]]: Determination of Geometry Independent Fracture Mechanics Values of Polymers. Int. J. of Fracture 68 (1994) R19–R22 | * [[Grellmann,_Wolfgang|Grellmann, W.]], [[Seidler,_Sabine|Seidler, S.]]: Determination of Geometry Independent Fracture Mechanics Values of Polymers. Int. J. of Fracture 68 (1994) R19–R22 | ||
* Grellmann, W., [[Seidler,_Sabine|Seidler, S.]], Hesse, W.: Prozedur zur Ermittlung des Risswiderstandverhaltens mit dem instrumentierten Kerbschlagbiegeversuch. In: Grellmann, W., Seidler, S.: Deformation und Bruchverhalten von Kunststoffen. Springer Verlag, Berlin Heidelberg (1998) S. 75–90, (ISBN 3-540-63671-4; [[AMK-Büchersammlung]] unter A 6) | * Grellmann, W., [[Seidler,_Sabine|Seidler, S.]], Hesse, W.: Prozedur zur Ermittlung des Risswiderstandverhaltens mit dem instrumentierten Kerbschlagbiegeversuch. In: Grellmann, W., Seidler, S.: Deformation und Bruchverhalten von Kunststoffen. Springer Verlag, Berlin Heidelberg (1998) S. 75–90, (ISBN 3-540-63671-4; [[AMK-Büchersammlung]] unter A 6) | ||
[[Kategorie:Bruchmechanik]] | [[Kategorie:Bruchmechanik]] | ||
Aktuelle Version vom 8. Januar 2026, 11:47 Uhr
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Geometriekriterium
Geometriekriterium, Bruchzähigkeit
Bei linear-elastischer Betrachtungsweise erfolgt die Abschätzung der Geometriegrößen B, a und der Ligamentausdehnung (W–a) über die empirisch ermittelte Beziehung
mit
| y | Streckspannung (Streckgrenze). |
Die Geometriekonstante ist werkstoffabhängig.
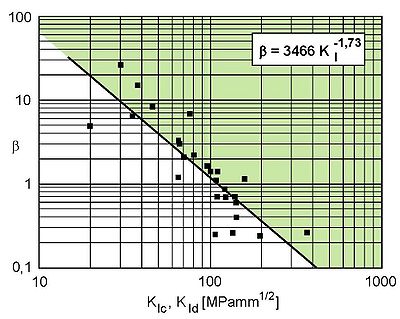
Experimentelle Ergebnisse bezüglich des Einflusses der Prüfkörperdicke B auf die bruchmechanischen Kennwerte (siehe Bruchmechanische Prüfung) für Kunststoffe liegen in der Literatur vor. In Bild 1 wird die Abhängigkeit des Koeffizienten nach obiger Gleichung von der bei quasistatischer und schlagartiger Beanspruchung (siehe: Schlagbeanspruchung Kunststoffe) bestimmten Bruchzähigkeit für verschiedene Kunststoffe gezeigt. Der dargestellte Zusammenhang wurde auf der Grundlage experimentell ermittelter Dicken- und a/W-Abhängigkeiten erstellt und besitzt einen hohen Verallgemeinerungsgrad, da sich unabhängig von der Beanspruchungsart (quasistatisch, schlagartig) und dem Werkstoffversagen (stabil, instabil) ein gemeinsamer Zusammenhang ergibt (siehe: Rissausbreitung).
| Bild 1: | Abhängigkeit des Koeffizienten von der Bruchzähigkeit KIc, KId für verschiedenen Kunststoffe |
Literaturhinweise
- Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig Stuttgart (1993) (ISBN 3-342-00659-5; siehe AMK-Büchersammlung unter E 29-3)
- Anderson, T. L.: Fracture Mechanics. Fundamentals and Applications. 3rd Ed., CRC Press, Boca Raton (2005) (ISBN 978-0849342608; siehe AMK-Büchersammlung unter E 8-2)), DOI: https://doi.org/10.1201/9781315370293
- Grellmann, W., Seidler, S., Lach, R.: Geometrieunabhängige bruchmechanische Werkstoffkenngrößen – Voraussetzung für die Zähigkeitscharakterisierung von Kunststoffen. Materialwissenschaften und Werkstofftechnik 32 (2001) 552–561
- Akay, M.: Fracture Mechanics Properties. In: Brown, R. P. (Ed.): Handbook of Polymer Testing. Marcel Dekker Inc., New York (1999) 533–588 (ISBN 978-0824701710; siehe AMK-Büchersammlung unter C 5)
- Williams, J. G.: Fracture Mechanics of Polymers. Ellis Horwood Ltd., Publisher (1984) (ISBN 978-0470-20013-1; siehe AMK-Büchersammlung unter E 42)
Geometriekriterium, J-Integral-Konzept
Auf Grund des für Kunststoffe typischen elastisch-plastischen Werkstoffverhaltens, insbesondere mit abnehmender Prüfkörperdicke, abnehmender Beanspruchungsgeschwindigkeit und zunehmender Temperatur, und den Grenzen für die Anwendbarkeit der linear-elastischen Bruchmechanik, ist es notwendig, das J-Integral-Konzept zur Beschreibung der Geometrieabhängigkeit heranzuziehen. Die kritischen J-Werte sind geometrieunabhängig, wenn das Kriterium
mit
| werkstoffabhängige Konstante des Geometriekriterium des J-Integral-Konzeptes |
erfüllt ist.
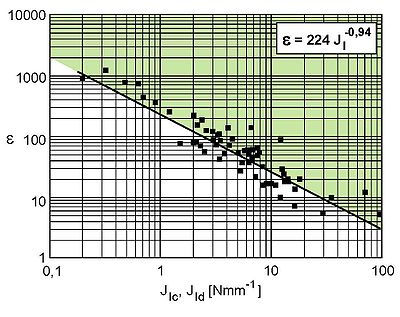
Für die Geometriekonstante aus diesem Kriterium ergibt sich aus Bild 2 eine Tendenz zur Abnahme mit zunehmender Zähigkeit, wonach , ebenso wie die Geometriekonstante , als eine werkstoffabhängige Größe angesehen werden muss und die Werte zwischen 5 und 1220 annehmen kann, die für schlagartige Beanspruchung jeweils Maximalwerte darstellen.
| Bild 2: | Abhängigkeit der Koeffizienten vom J-Wert für verschiedene Kunststoffe |
Die Kenntnis des allgemeinen -J-Zusammenhangs erlaubt die Abschätzung der erforderlichen Prüfkörperdicken. Der Vorteil der Bestimmung bruchmechanischer Kennwerte bei schlagartiger Beanspruchung liegt in der Möglichkeit, bereits bei niedrigen Prüfkörperdicken geometrieunabhängige Werte zu erhalten.
Literaturhinweise
- Grellmann, W., Seidler, S., Lach, R.: Geometrieunabhängige bruchmechanische Werkstoffkenngrößen – Voraussetzung für die Zähigkeitscharakterisierung von Kunststoffen. Materialwissenschaften und Werkstofftechnik 32 (2001) 552–561
- Grellmann, W.: Neue Entwicklungstendenzen bei der bruchmechanischen Zähigkeitscharakterisierung von Kunststoffen und Verbunden. In: Grellmann, W., Seidler, S.: Deformation und Bruchverhalten von Kunststoffen. Springer Verlag, Berlin Heidelberg (1998) S. 3–26, (ISBN 3-540-63671-4; e-Book (2014): ISBN 978-3-642-58766-5; siehe AMK-Büchersammlung unter A 6)
Geometriekriterium, Rissöffnungsverschiebung
Die Abschätzung der Anforderungen an die Prüfkörpergeometrie erfolgt bei Anwendung des Crack-Tip-Opening Displacement(CTOD)-Konzeptes
| . |
mit
| werkstoffabhängige Konstante des Geometriekriteriums des CTOD-Konzeptes |
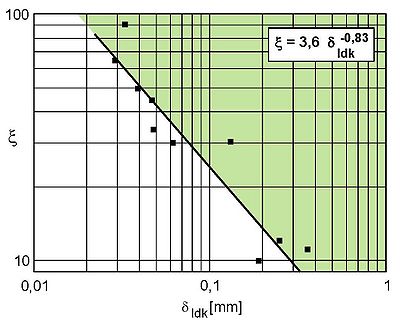
| Bild 3: | Abhängigkeit des Koeffizienten von der kritischen Rissöffnung Idk |
Neben dem J-Integral-Konzept wird insbesondere zur Beschreibung verformungsdeterminierter Bruchvorgänge das CTOD-Konzept verwendet. Voraussetzung für die Ermittlung kritischer Rissöffnungen ist die Ausbildung eines quasistatischen Spannungszustandes. Auf der Basis des Plastic-Hinge-Modells wird bei schlagartiger Beanspruchung die kritische Rissöffnung ermittelt, die bei B = 4 mm für a/W > 0,2 unabhängig vom a/W-Verhältnis ist. Aus Bild 3 wird ersichtlich, dass man -Werte zwischen 10 und 90 annehmen kann und bei noch unbekannter Abschätzung der notwendigen Kerbtiefe bzw. Prüfkörperdicke eine erhebliche Überschätzung der erforderlichen Mindestprüfkörperabmessungen möglich ist.
Siehe auch
Literaturhinweise
- Grellmann, W., Seidler, S.: Determination of Geometry Independent Fracture Mechanics Values of Polymers. Int. J. of Fracture 68 (1994) R19–R22
- Grellmann, W., Seidler, S., Hesse, W.: Prozedur zur Ermittlung des Risswiderstandverhaltens mit dem instrumentierten Kerbschlagbiegeversuch. In: Grellmann, W., Seidler, S.: Deformation und Bruchverhalten von Kunststoffen. Springer Verlag, Berlin Heidelberg (1998) S. 75–90, (ISBN 3-540-63671-4; AMK-Büchersammlung unter A 6)