ENF-Prüfkörper: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „{{PSM_Infobox}} <span style="font-size:1.2em;font-weight:bold;">ENF-Prüfkörper</span> __FORCETOC__ ==Allgemeines== Die angelsächsische Abkürzung ENF steht f…“ |
Keine Bearbeitungszusammenfassung |
||
| Zeile 39: | Zeile 39: | ||
|C<sub>b</sub> | |C<sub>b</sub> | ||
| | | | ||
|Nachgiebigkeit des Prüfkörpers bei F | |[[Probennachgiebigkeit|Nachgiebigkeit]] des Prüfkörpers bei F | ||
|- | |- | ||
|W | |W | ||
| Zeile 50: | Zeile 50: | ||
|} | |} | ||
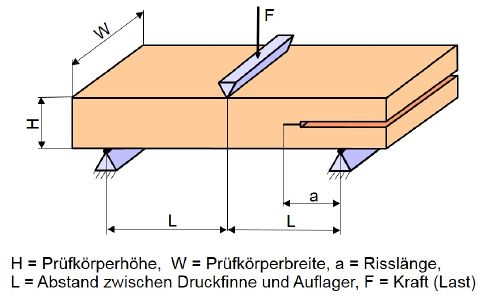
Als konservative Abschätzung der Nachgiebigkeit ist in vielen Fällen die einfache Balkentheorie ausreichend; der Versuch wird mit einer Dreipunktbiegevorrichtung und einem definierten Anfangsriss von 25 mm durchgeführt. | Als konservative Abschätzung der Nachgiebigkeit ist in vielen Fällen die einfache Balkentheorie ausreichend; der Versuch wird mit einer [[Biegeversuch#Die_Methode_der_Dreipunktbiegepr.C3.BCfung|Dreipunktbiegevorrichtung]] und einem definierten Anfangsriss von 25 mm durchgeführt. | ||
[[Datei:enf_jis.jpg|400px]] | [[Datei:enf_jis.jpg|400px]] | ||
| Zeile 83: | Zeile 83: | ||
|L | |L | ||
| | | | ||
|halber Auflagerabstand | |halber [[Auflagerabstand]] | ||
|} | |} | ||
Version vom 16. Februar 2018, 15:03 Uhr
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
ENF-Prüfkörper
Allgemeines
Die angelsächsische Abkürzung ENF steht für "End-Notched Flexure".
Der ENF-Prüfkörper wird zur Bestimmung der interlaminaren Risszähigkeiten von Mode II-Belastung verwendet. Als bruchmechanische Kenngröße wird eine kritische Energiefreisetzungsrate in ebener Dehnung ermittelt. Es wird eine Scherbeanspruchung ohne große Reibung zwischen den Oberflächen eines Risses vorausgesetzt. Schubspannungen und -dehnungen vor der Rissspitze (siehe auch Rissöffnung) können Einfluss auf die Berechnung der Energiefreisetzungsrate haben.
Prüfkörperform
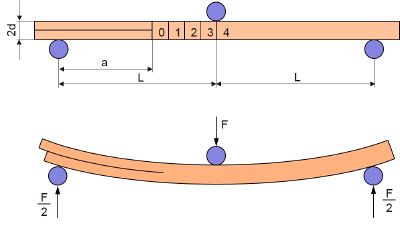
| Bild 1: | Schematische Darstellung des ENF-Prüfkörpers |
Bestimmungsgleichung
Zur Berechnung der Energiefreisetzungsrate GIIc für EDZ gilt die Gleichung
mit:
| a | Risslänge | |
| F | Versagenskraft (Fmax) | |
| Cb | Nachgiebigkeit des Prüfkörpers bei F | |
| W | Prüfkörperbreite | |
| L | Abstand zwischen Druckfinne und Auflage |
Als konservative Abschätzung der Nachgiebigkeit ist in vielen Fällen die einfache Balkentheorie ausreichend; der Versuch wird mit einer Dreipunktbiegevorrichtung und einem definierten Anfangsriss von 25 mm durchgeführt.
| Bild 2: | ENF-Prüfkörper im unbelasteten und belasteten Zustand nach JIS K 7086 |
Die Nachgiebigkeit kann experimentell bestimmt oder berechnet werden nach
mit:
| E | Biegemodul in axialer Richtung | |
| d | halbe Balkenhöhe | |
| f | Durchbiegung | |
| L | halber Auflagerabstand |
Durch Einsetzen dieser Gleichungen erhält man eine berechnete Energiefreisetzungsrate
Eine umfangreiche Zusammenstellung von geeigneten Prüfkörpern für bruchmechanische Untersuchungen an Kunststoffen und Verbundwerkstoffen ist in Prüfkörper für bruchmechanische Prüfungen enthalten.
Literaturhinweise
| Carlsson, L. A., Pipes, R. B.: Hochleistungsverbundwerkstoffe, B. G. Teubner, Stuttgart (1989) | |
| Valisetly, R. R., Chamis, C. C.: ASTM STP 972 (1988) 41–72 (Composite Materials. Testing and Design / Eighth Conference) | |
| Russel, A. J., Street, K. N.: Moisture and Temperature Effects on the Mixed Mode Delamination. Fracture of Unidirectional Graphite / Epoxy. Delamination and Deponding of Materials, ASTM STP 876 (1985) 349 | |
| Hodgkinson, J. M. (Ed.): Mechanical Testing of Advanced Fibre Composites, Woodhead Publishing, Cambridge (2000) | |
| Altstädt, V.: Prüfung von Verbundwerkstoffen. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 582/583 (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18) |

![{\displaystyle G_{IIc}={\frac {9\cdot F^{2}\cdot a^{2}\cdot C_{b}}{2\cdot W\left(2\cdot L^{3}+3\cdot a^{3}\right)}}\left[{\frac {J}{m^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23647dd84791008be86e6b7cbcc81bfedba0eec7)