Auflösungsvermögen Mikroskop: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 165: | Zeile 165: | ||
|-valign="top" | |-valign="top" | ||
|[1] | |[1] | ||
|Kämpf, G.: Charakterisierung von Kunststoffen mit physikalischen Methoden. Verfahren und praktische Anwendung. Carl Hanser Verlag, München Wien (1982), S. 19–21, (ISBN 3-446-13382- | |Kämpf, G.: Charakterisierung von Kunststoffen mit physikalischen Methoden. Verfahren und praktische Anwendung. Carl Hanser Verlag, München Wien (1982), S. 19–21, (ISBN 978-3-446-13382-2; siehe [[AMK-Büchersammlung]] unter D 4) | ||
|} | |} | ||
Version vom 23. März 2023, 11:23 Uhr
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Auflösungsvermögen Mikroskop
Untersuchungsmethoden in der Mikroskopie
Zur Charakterisierung der Struktur und Morphologie (siehe: Mikroskopische Struktur) von Kunststoffen werden in der Kunststoffprüfung und Diagnostik die Methoden der Licht- und Elektronenmikroskopie eingesetzt. Dabei werden die nachfolgenden Untersuchungsmethoden bevorzugt verwendet:
- Elektronenmikroskopie
- Energiedispersive Röntgenspektroskopie – EDX
- in-situ-Ultramikrotomie
- Low-Vacuum-Rasterelektronenmikroskopie (siehe Umgebungs-REM)
- Mikrotomie
- Rasterkraftmikroskopie
- Rasterelektronenmikroskopie
- Umgebungs-REM (ESEM)
- Transmissionselektronenmikroskopie
Optische Parameter zur Beschreibung der Leistungsfähigkeit von Lichtmikroskopen
Die optische Leistungsfähigkeit von Mikroskopen wird durch die folgenden Parameter charakterisiert [1]:
- Auflösungsvermögen
- Förderliche Vergrößerung
- Schärfentiefe
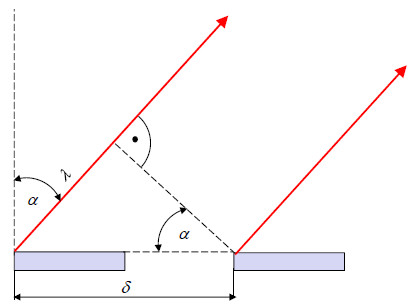
Nach der ABBE’schen Theorie gelten für die Beugung von Lichtwellen am Spalt (Gitter) folgende Beziehungen:
| (1) |
mit
| λ | Wellenlänge des Lichtes | |
| δ | Auflösungsvermögen = kleinster, noch trennbarer Abstand zweier Punkte |
| Bild 1: | Beugung von Lichtwellen |
Für das Auflösungsvermögen des Lichtmikroskopes ergibt sich:
- für Vakuum (bzw. ~ Luft):
| (2) |
- im Medium mit Brechungsindex n (z. B. Immersionsöl):
| (3) |
mit
| n ⋅ sin α | numerische Apertur |
Für Lichtmikroskope gilt:
α → 90° entspricht sin α → 1,
für n = 1,4 (Immersionsöl) und λ = 0,55 µm (grünes Licht) wird
, d. h. das Auflösungsvermögen des Lichtmikroskopes (mit Ölimmersion) liegt bei 0,4 µm.
Auflösungsvermögen in der Elektronenmikroskopie
Für Transmissionselektronenmikroskope gelten für das erreichbare Auflösungsvermögen die folgenden Beziehungen:
Berechnung der Wellenlänge schnell bewegter Elektronen λEI:
| Energiegleichung | (4) |
| (5) |
mit
| e | Ladung des Elektrons | |
| m | Masse des Elektrons | |
| v | Geschwindigkeit | |
| U | Beschleunigungsspannung |
Für die Wellenlänge von Materiewellen gilt die DE BROGLIE’sche Gleichung:
| (6) |
mit
| h | PLANCK’sches Wirkungsquantum |
Zusammen ergibt sich:
| (7) |
Wegen der relativistischen Geschwindigkeitskorrektur liegen die tatsächlich erreichten Wellenlängen etwas höher;
Beispiele:
U = 40 kV: λEI = 0,0060 nm
U = 100 kV: λEI = 0,0037 nm
U = 200 kV: λEI = 0,0025 nm
Wegen der endlichen Linsenfehler elektromagnetischer Linsen (sphärischer Fehler, Öffnungsfehler, Beugungsfehler u. a.) liegen die erreichbaren Werte für die numerische Apertur α bei ca. 10-2 bis 10-3, das Punkt-Auflösungsvermögen erreicht nur Werte von ca. 0,2 bis 04 nm [1].
Literaturhinweis
| [1] | Kämpf, G.: Charakterisierung von Kunststoffen mit physikalischen Methoden. Verfahren und praktische Anwendung. Carl Hanser Verlag, München Wien (1982), S. 19–21, (ISBN 978-3-446-13382-2; siehe AMK-Büchersammlung unter D 4) |