Kriechverhalten Zeitstandbiegeversuch: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 67: | Zeile 67: | ||
|-valign="top" | |-valign="top" | ||
|[2] | |[2] | ||
|DIN EN ISO 178 ( | |DIN EN ISO 178 (2019-08): Kunststoffe – Bestimmung der Biegeeigenschaften | ||
|-valign="top" | |-valign="top" | ||
|[3] | |[3] | ||
Version vom 28. August 2019, 12:31 Uhr
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Kriechverhalten Zeitstandbiegeversuch
Allgemeines
Das Kriechverhalten von Kunststoffen kann unter Zug-, Biege- und Druckbeanspruchung oder mit der registrierenden Härtemessung ermittelt werden. Für die experimentelle Bestimmung des Kriech- bzw. Langzeitverhaltens kann auch der Zeitstandbiegeversuch genutzt werden [1]. Dieser Versuch wird speziell für die Untersuchung langzeitiger Beanspruchungen bei Bau- und Maschinenteilen verwendet, um das zeitabhängige Verformungs- und Festigkeitsverhalten beurteilen zu können.
Ermittlung der zeitabhängigen Durchbiegung
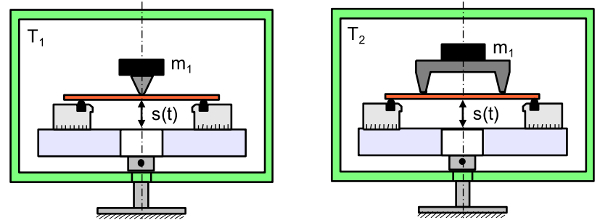
Die grundlegende messtechnische Voraussetzung besteht in der Ermittlung der zeitabhängigen Durchbiegung s(t) am Prüfkörper, die mit mechanischen Extensometern (Flexometer) oder optoelektronischen Dehnmesssystemen (Videoextensometer, Laserextensometer) erfasst werden kann (Bild 1). Es kann aber auch die Traversenwegmessung angewandt werden, wobei hier aber die Maschinennachgiebigkeit der genutzten Konfiguration bekannt sein sollte.
| Bild 1: | Schematische Darstellung der Erfassung der zeitabhängigen Durchbiegung von Kunststoffen im Zeitstandbiegeversuch mittels Zeitstandprüfstand |
Durchführung des Zeitstandbiegeversuches
Zur Erzeugung der erforderlichen Belastungsstufen können Zeitstandprüfstände oder Universalprüfmaschinen verwendet werden, wobei diese zur Sicherung konstanter Prüfbedingungen mit Temperierkammern ausgestattet sein müssen. Unter ökonomischen und zeitlichen Aspekten sollten dabei mindestens 10 Einzelprüfstände verfügbar sein, die entweder mit veränderbarer Belastung bei gleicher Temperatur oder mit identischer Beanspruchungsstufe aber variierenden Temperaturen betrieben werden. Bei Nutzung von Universalprüfmaschinen müssen die Versuche unter Kraftregelung durchgeführt werden, da ansonsten die stattfindende Spannungsrelaxation die Prüfbedingungen, speziell die Belastung, verändern würde. Grundsätzlich können die Zeitstandbiegeversuche in der Drei- oder Vierpunktbiegeanordnung realisiert werden, wobei aber zumeist der technisch einfachere und genormte Dreipunktbiegeversuch bevorzugt wird (Bild 1).
Definition der zeitabhängigen Kriechrandfaserdehnung
Für die Prüfungen werden prismatische Prüfkörper mit den Abmessungen 80 x 10 x 4 mm3 in Übereinstimmung mit der DIN EN ISO 178 [2] verwendet, wobei die Normen DIN EN ISO 293 bis DIN EN ISO 295 [3–5] zu beachten sind. Die Präparation der Prüfkörper sollte dabei entsprechend der Forderungen der DIN EN ISO 2818 [6] erfolgen. Die Zeitstandbiegeversuche werden heute üblicherweise konform zu der Norm DIN EN ISO 899-2 [7] im Dreipunktbiegeverfahren durchgeführt. In der zurückgezogenen Norm DIN 54852 [8] war dagegen das Drei- und Vierpunktbiegeverfahren zur Ermittlung der Langzeiteigenschaften von Kunststoffen erlaubt. Nach der stoßfreien Lastaufbringung wird dann kontinuierlich die Prüfkörperdurchbiegung st(t) zu den von der Norm [7] vorgegebenen Zeiten bis zum Bruch oder einem definierten Zeitwert registriert. Die aufgebrachte Lastspannung ist entsprechend Gl. (1) über die applizierte Kraft oder die äquivalente Masse definiert. Die zeitabhängige Kriechrandfaserdehnung berechnet sich aus der Durchbiegung st nach Gl. (2).
| (1) |
| (2) |
Die Kennwerte des Zeitstandbeigeversuches
In Analogie zum Zeitstandzugversuch werden die aufgezeichneten halblogarithmischen Kriechkurven (Zeit-Dehnlinien) entsprechend der Auswerteprozedur [7] in das Zeitstandschaubild, das isochrone-Spannungs-Dehnungs-Diagramm und die Kriechmodul-Zeit-Kurven umgewandelt. Aus diesen Kurven lassen sich dann die Kennwerte des Zeitstandbiegeversuchs nach der Norm [7] berechnen. Im Fall der Dreipunktbiegung ergibt sich der Kriechmodul nach Gl. 3.
| (3) |
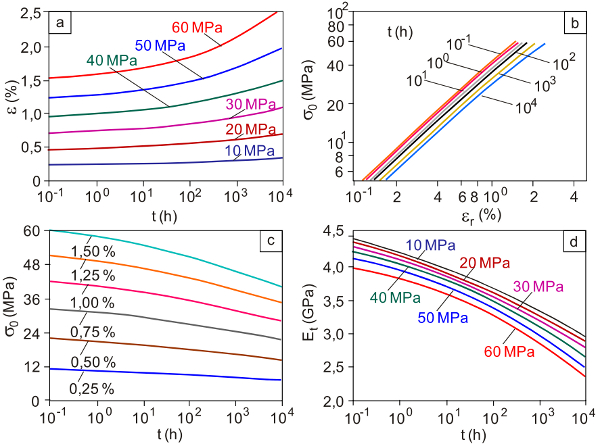
| Bild 2: | Zeitstandbiegeverhalten von PVC bei verschiedenen Belastungen [1]: Kriechkurven a), isochrones Biegespannungs-Randfaserdehnungs-Diagramm b), Zeitstandschaubild c) und Biegekriechmodul-Kurven d) |
Ein Beispiel für Polyvinylchlorid (Kurzzeichen: PVC) für eine Beanspruchungsdauer von bis zu 104 h ist in dem Bild 2 dargestellt. Weitere Informationen zu grafischen und tabellarischen Biegekriechdaten von Kunststoffen sind in [9] enthalten.
Literaturhinweise
| [1] | Höninger, H.: Statisches Langzeitverhalten. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 182–192 (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18) |
| [2] | DIN EN ISO 178 (2019-08): Kunststoffe – Bestimmung der Biegeeigenschaften |
| [3] | DIN EN ISO 293 (2005-10): Kunststoffe – Formgepresste Probekörper aus Thermoplasten |
| [4] | DIN EN ISO 294-1 (2017-09): Kunststoffe – Spritzgießen von Probekörpern aus Thermoplasten – Teil 1: Allgemeine Grundlagen und Herstellung von Vielzweckprobekörpern und Stäben |
| [5] | DIN EN ISO 295 (2004-05): Kunststoffe – Pressen von Probekörpern aus duroplastischen Werkstoffen |
| [6] | DIN EN ISO 2818 (2018-10): Kunststoffe – Herstellung von Probekörpern durch mechanische Bearbeitung (Entwurf) |
| [7] | DIN EN ISO 899-2 (2015-06): Kunststoffe – Bestimmung des Kriechverhaltens – Teil 2: Zeitstand-Biegeversuch bei Dreipunkt-Belastung |
| [8] | DIN 54852 (1986-09): Prüfung von Kunststoffen – Zeitstand-Biegeversuch bei Dreipunkt- und Vierpunktbelastung (zurückgezogen) |
| [9] | Bierögel, C., Grellmann, W.: Long-term Loading Test. In: Grellmann, W., Seidler, S. (Hrsg.): Mechanical and Thermomechanical Properties of Polymers. Landoldt Börnstein. Volume VIII/6A3, Springer Verlag, Berlin (2014) S. 286−331 |