Scherviskosität: Unterschied zwischen den Versionen
Posch (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 87: | Zeile 87: | ||
|-valign="top" | |-valign="top" | ||
|[1] | |[1] | ||
|[[Radusch,_Hans-Joachim|Radusch, H.-J.]]: Bestimmung verarbeitungsrelevanter Eigenschaften. In: [[Grellmann,_Wolfgang|Grellmann, W.]], [[Seidler,_Sabine|Seidler, S.]] (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 47–50, (ISBN 978-446-44350-1; siehe [[AMK-Büchersammlung]] unter A 18) | |[[Radusch,_Hans-Joachim|Radusch, H.-J.]]: Bestimmung verarbeitungsrelevanter Eigenschaften. In: [[Grellmann,_Wolfgang|Grellmann, W.]], [[Seidler,_Sabine|Seidler, S.]] (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 47–50, (ISBN 978-3-446-44350-1; siehe [[AMK-Büchersammlung]] unter A 18) | ||
|-valign="top" | |-valign="top" | ||
|[2] | |[2] | ||
|Kulicke, W.-M.: Fließverhalten von Stoffen und Stoffgemischen. Hüthing & Wepf Verlag, Basel Heidelberg New York (1986) | |Kulicke, W.-M.: Fließverhalten von Stoffen und Stoffgemischen. Hüthing & Wepf Verlag, Basel Heidelberg New York (1986) (ISBN 3-85738-115-4) | ||
|} | |} | ||
[[Kategorie:Verarbeitungsrelevante Eigenschaften]] | [[Kategorie:Verarbeitungsrelevante Eigenschaften]] | ||
Aktuelle Version vom 4. August 2023, 11:02 Uhr
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Scherviskosität
Fließverhalten von Fluiden
Die Fließfähigkeit oder das Fließverhalten von Fluiden wird durch die Viskosität charakterisiert, die den inneren Widerstand des Fluids gegen eine von außen einwirkende Beanspruchung beschreibt. Entsprechend der Beanspruchungsart wird zwischen Scher- und Dehnviskosität unterschieden [1]. In der elementaren Fluidmechanik ist die absolute Scherviskosität durch die NEWTON’sche Gleichung definiert:
| (1) |
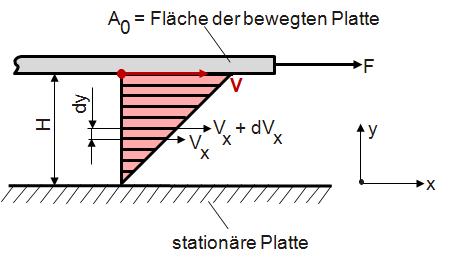
Dabei ist in einer Zweiplattenanordnung entsprechend Bild 1 yx = F/A0 die Schubspannung, die sich beim Bewegen einer Platte mit der Fläche A0 und der Geschwindigkeit vx über ein Fluid, das sich auf einer feststehenden Platte befindet, ergibt. Für ein NEWTON’sches Medium sind die Schubspannung yx und der resultierende Geschwindigkeitsgradient x = dvx/dy (Schergeschwindigkeit) direkt proportional. Die Proportionalitätskonstante ist die Größe , die NEWTON’sche Viskosität.
| Bild 1: | Geschwindigkeitsprofil eines NEWTON’schen Fluids bei zweidimensionalem Scherfließen (Zweiplattenmodell) |
NEWTON'sches und nicht-NEWTON'sches Fließverhalten
NEWTON’sche Fluide, d. h. Flüssigkeiten bei denen die Viskosität bei Variation der Schergeschwindigkeit konstant bleibt, sind Wasser, Lösungsmittel, Mineralöl oder verdünnte Polymerlösungen. Polymerschmelzen zeigen in der Regel nur bei sehr niedrigen Schergeschwindigkeiten NEWTON’sches Verhalten.
In realen Verarbeitungsprozessen wie der Extrusion oder dem Spritzgießen, bei denen höhere Schergeschwindigkeiten in hochviskosen Schmelzen auftreten, liegt nicht-NEWTON’sches Fließen vor [2]. Es besteht keine direkte Proportionalität zwischen Schubspannung und Schergeschwindigkeit und die Viskosität ist keine Konstante mehr.
Fließkurve
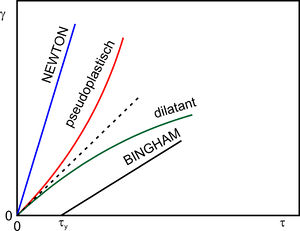
Die meisten Polymere verhalten sich im Schmelzezustand auf Grund ihres makromolekularen Charakters strukturviskos bzw. pseudoplastisch, d. h. mit ansteigender Schergeschwindigkeit verringert sich die Viskosität kontinuierlich und die Schubspannung steigt degressiv (siehe Bild 2). Trägt man log über log auf, zeigen die meisten Polymerschmelzen bei konstanter Temperatur und konstantem Druck über einen weiten Bereich eine Gerade oder eine leicht gekrümmte Linie, d. h. eine exponentielle Abhängigkeit. Die Beziehung zwischen Schubspannung und Scherdeformation kann daher für die meisten Polymerschmelzen in erster Näherung durch das einfache Potenzgesetz nach OSTWALD und de WAELE beschrieben werden:
| (2) |
| (3) |
| Bild 2: | Fließkurven unterschiedlicher Fluide |
K ist der Konsistenzkoeffizient und entspricht einer Bezugsviskosität. Der Exponent n wird als Fließexponent bezeichnet. Er ist nicht konstant, sondern abhängig von der Schergeschwindigkeit und der Temperatur. Für pseudoplastische Fluide ist n kleiner 1. Wenn die Schergeschwindigkeit gegen Null geht oder sehr groß wird, kann dieses Potenzgesetz das reale Verhalten jedoch nicht mehr approximieren.
Ein weiterer Ansatz, der den Zusammenhang zwischen Schubspannung und Scherdeformation besser beschreibt, ist das empirische CARREAU-Modell:
| (4) |
Darin sind η0 und η∞ die Viskositäten bei sehr niedrigen und sehr hohen Schergeschwindigkeiten, ist eine Zeitkonstante.
Der CARREAU-Ansatz kann auch in der Form
| (5) |
aT: Temperaturverschiebungsfaktor
geschrieben werden. Hierbei sind A, B und C empirisch zu bestimmende Stoffkonstanten, die aus einem experimentell bestimmten Verlauf von log über log ermittelt werden können (Bild 3). Neben dem NEWTON’schen und pseudoplastischen Verhalten können Fluide auch dilatantes Verhalten oder das Fließverhalten eines BINGHAM-Körpers zeigen (Bild 2). Im Gegensatz zu pseudoplastischen Fluiden zeigen dilatante Stoffe mit steigender Schergeschwindigkeit eine Erhöhung der Viskosität. Das BINGHAM-Verhalten ist charakterisiert durch die Existenz einer Fließgrenze, d. h. das Fließen setzt erst ab einer bestimmten Scherspannung ein.
| Bild 3: | Konstanten im CARREAU-Ansatz |
Literaturhinweise
| [1] | Radusch, H.-J.: Bestimmung verarbeitungsrelevanter Eigenschaften. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 47–50, (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18) |
| [2] | Kulicke, W.-M.: Fließverhalten von Stoffen und Stoffgemischen. Hüthing & Wepf Verlag, Basel Heidelberg New York (1986) (ISBN 3-85738-115-4) |







![{\displaystyle {\frac {\eta -\eta _{\infty }}{\eta _{0}-\eta _{\infty }}}\,=\,\left[1-\left(\lambda {\dot {\gamma }}\right)^{2}\right]^{\frac {\left(n-1\right)}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2792f54b291c1546d603febaadbb5dbe2528b4dd)


