Bruchverhalten: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
{{PSM_Infobox}} | {{PSM_Infobox}} | ||
<span style="font-size:1.2em;font-weight:bold;">Bruchverhalten, Kunststoffe</span> | <span style="font-size:1.2em;font-weight:bold;">Bruchverhalten, Kunststoffe</span> | ||
__FORCETOC__ | |||
==Allgemeines== | |||
[[Polymer]]e Werkstoffe zeigen je nach Typ und [[Beanspruchung]]sbedingungen ein sehr unterschiedliches Verhalten beim [[Bruch]]. | [[Polymer]]e Werkstoffe zeigen je nach Typ und [[Beanspruchung]]sbedingungen ein sehr unterschiedliches Verhalten beim [[Bruch]]. | ||
Einige teilkristalline Polymere wie Polyamid ([[Kurzzeichen]]: PA), Polyethylen ([[Kurzzeichen]]: PE) und Polypropylen ([[Kurzzeichen]]: PP) können bis zu einem Dehnungsverhältnis von <math>\lambda</math> = 20 kaltgezogen werden, wobei sich eine stabile Einschnürung entlang des [[Prüfkörper]]s bewegt. | Einige teilkristalline Polymere wie Polyamid ([[Kurzzeichen]]: PA), Polyethylen ([[Kurzzeichen]]: PE) und Polypropylen ([[Kurzzeichen]]: PP) können bis zu einem Dehnungsverhältnis von <math>\lambda</math> = 20 kaltgezogen werden, wobei sich eine stabile Einschnürung entlang des [[Prüfkörper]]s bewegt. | ||
Viele amorphe Kunststoffe (z.B. Polystyrol ([[Kurzzeichen]]: PS) oder Polymethylmethacrylat ([[Kurzzeichen]]: PMMA) sind bei Zugbeanspruchung spröd, verformen sich aber bei Druckspannungen oder reiner Scherbeanspruchung plastisch. Ebenso zeigen Epoxidharze ([[Kurzzeichen]]: EP) in Kompression einen hohen Grad an Duktilität. Typische Vertreter eines duktilen und zähen Bruchverhaltens sind z.B. PP, PE oder auch PA. | Viele amorphe Kunststoffe (z. B. Polystyrol ([[Kurzzeichen]]: PS) oder Polymethylmethacrylat ([[Kurzzeichen]]: PMMA) sind bei Zugbeanspruchung spröd, verformen sich aber bei Druckspannungen oder reiner Scherbeanspruchung plastisch. Ebenso zeigen Epoxidharze ([[Kurzzeichen]]: EP) in Kompression einen hohen Grad an Duktilität. Typische Vertreter eines duktilen und zähen Bruchverhaltens sind z. B. PP, PE oder auch PA. | ||
==Typische Mechanismen der plastischen Deformation== | |||
Die '''[[plastische Deformation]]''' tritt bei duktilen Polymeren in zwei Formen auf: | Die '''[[plastische Deformation]]''' tritt bei duktilen Polymeren in zwei Formen auf: | ||
Die '''Scherdeformation''' (shear yielding), d.h. die Schubspannungsfließzonenbildung, die eine starke Formänderung ohne Volumenänderung hervorruft. Scherdeformationen zeigen viele teilkristalline Polymere bei Zugbeanspruchung, Raumtemperatur (RT) und Prüfung an Luft (Bild). | Die '''Scherdeformation''' (shear yielding), d. h. die Schubspannungsfließzonenbildung, die eine starke Formänderung ohne Volumenänderung hervorruft. Scherdeformationen zeigen viele teilkristalline Polymere bei Zugbeanspruchung, Raumtemperatur (RT) und Prüfung an Luft (Bild) (siehe: [[Scherbandbildung]]). | ||
Das '''[[Crazing]]''' (Normalspannungsfließzonenbildung), d.h. der Bildung von Hohlräumen. Dieser Prozess verursacht eine starke [[Dichte]]änderung und tritt bei Blends und praktisch allen glasartigen [[Polymer]]en auf. Bei geringen Beanspruchungen findet man häufig einzelne isolierte Crazes ('''Bild'''). | Das '''[[Crazing]]''' (Normalspannungsfließzonenbildung), d. h. der Bildung von Hohlräumen. Dieser Prozess verursacht eine starke [[Dichte]]änderung und tritt bei [[Polymerblends|Blends]] und praktisch allen glasartigen [[Polymer]]en auf. Bei geringen Beanspruchungen findet man häufig einzelne isolierte Crazes ('''Bild'''). | ||
[[Datei:bruchverhalten_kunststoffe.png|600px]] | [[Datei:bruchverhalten_kunststoffe.png|600px]] | ||
| Zeile 19: | Zeile 22: | ||
|width="50px"|'''Bild''': | |width="50px"|'''Bild''': | ||
|width="600px" |Schematische Darstellung von Deformationserscheinung in amorphen Kunststoffen | |width="600px" |Schematische Darstellung von Deformationserscheinung in amorphen Kunststoffen | ||
(a) Crazes <br> | (a) Crazes (siehe: [[Crazing]]) <br> | ||
(b) Scherband | (b) Scherband (siehe: [[Scherbandbildung]]) | ||
|} | |} | ||
Das Auftreten eines oder beider Mechanismen hängt von folgenden Bedingungen ab: | Das Auftreten eines oder beider Mechanismen hängt von folgenden Bedingungen ab: | ||
* Struktur des Makromoleküls | * Struktur des Makromoleküls | ||
* Kristallisationsgrade und Sphärolithgröße | * [[Kristallinität|Kristallisationsgrade]] und Sphärolithgröße (siehe: [[Sphärolithische Struktur]]) | ||
* Deformationsgrad | * Deformationsgrad | ||
* Vorhandensein einer zweiten Phase sowie der Testbedingungen | * Vorhandensein einer zweiten Phase sowie der Testbedingungen | ||
* Temperatur | * Temperatur | ||
* Verformungsgeschwindigkeit | * [[Verformungsgeschwindigkeit]] (siehe auch: [[Dehnrate Grundlagen]]) | ||
* dreiachsiger Spannungszustand | * dreiachsiger Spannungszustand | ||
* Umgebungsbedingungen | * Umgebungsbedingungen | ||
| Zeile 35: | Zeile 38: | ||
== Bruchverhalten, Kurzfaserverbunde == | == Bruchverhalten, Kurzfaserverbunde == | ||
Einsatz und Anwendungsgrenzen von | Einsatz und Anwendungsgrenzen von [[Kurzfaserverstärkte Verbundwerkstoffe|kurzfaserverstärkten Verbundwerkstoffen]] sind von der Forderung nach möglichst präziser Vorausbestimmung der zu erwartenden Verbundeigenschaft mitbestimmt. Die Vielfalt der Einflussfaktoren lässt eine umfassende Theorie der Mechanik polymerer [[Prüfung von Verbundwerkstoffen|Verbundwerkstoffe]] auch künftig nicht zu. Es erscheint daher am zweckmäßigsten, empirisch ermittelte Gesetzmäßigkeiten durch anwendungsgerechte, zielgerichtete Modelle in mathematisch einfachen Formen zu beschreiben. | ||
In der Literatur gibt es zahlreiche Bestrebungen, das | In der Literatur gibt es zahlreiche Bestrebungen, das [[Zähigkeit]]sverhalten von faserverstärkten Verbundwerkstoffen durch Modelle zu beschreiben [2, 3]. Wesentliche Grundannahme in diesen Modellen ist oft ein sprödes Werkstoffverhalten. Darauf aufbauend erfolgte die Modellierung des Zähigkeitsverhaltens über theoretische Konzepte, wobei Wechselwirkungsparameter häufig nicht berücksichtigt werden konnten. | ||
Allgemein ist der Versagensprozess von kurzfaserverstärkten Kunststoffen jedoch durch das Auftreten energiedissipativer Prozesse gekennzeichnet, wobei die im Bild dargestellten Mechanismen auftreten: | Allgemein ist der Versagensprozess von kurzfaserverstärkten Kunststoffen jedoch durch das Auftreten energiedissipativer Prozesse gekennzeichnet, wobei die im Bild dargestellten Mechanismen auftreten: | ||
| Zeile 44: | Zeile 47: | ||
* pull-out | * pull-out | ||
* debonding | * debonding | ||
* plastische Deformation und Matrixversagen | * [[Deformation#Plastische Deformation|plastische Deformation]] und Matrixversagen | ||
[[Datei:faserverbund.jpg|300px]] | [[Datei:faserverbund.jpg|300px]] | ||
| Zeile 50: | Zeile 53: | ||
== Bruchverhalten, Teilchenverbunde == | == Bruchverhalten, Teilchenverbunde == | ||
Eine Möglichkeit zur Modellierung der Brucharbeit, die bei instabiler [[Rissausbreitung]] und elastisch-plastischem Werkstoffverhalten in teilchengefüllten | Eine Möglichkeit zur Modellierung der Brucharbeit, die bei instabiler [[Rissausbreitung]] und elastisch-plastischem Werkstoffverhalten in teilchengefüllten [[Thermoplaste]]n verrichtet wird, zeigt das Modell von Bohse [4, 5]. | ||
In Analogie zu den Modellvorstellungen von Friedrich und Lauke [6] für Kurzfaserverbunde treten folgende Arbeitsanteile auf: | In Analogie zu den Modellvorstellungen von Friedrich und Lauke [6] für Kurzfaserverbunde treten folgende Arbeitsanteile auf: | ||
| Zeile 56: | Zeile 59: | ||
* Matrix/Teilchen-Ablösung | * Matrix/Teilchen-Ablösung | ||
* nicht lineare viskoelastische Matrixdeformation | * nicht lineare viskoelastische Matrixdeformation | ||
* plastische Deformation von Matrixfibrillen | * [[Deformation#Plastische Deformation|plastische Deformation]] von Matrixfibrillen | ||
* Fibrillenbruch | * Fibrillenbruch | ||
| Zeile 67: | Zeile 70: | ||
|-valign="top" | |-valign="top" | ||
|[1] | |[1] | ||
|Michler, G.H.: Kunststoff-Mikromechanik – Morphologie, Deformation und Bruchmechanismen von polymeren Werkstoffen. Carl Hanser Verlag, München Wien (1992) ISBN 3-446-170685 (siehe [[AMK-Büchersammlung]] unter F 4) | |Michler, G. H.: Kunststoff-Mikromechanik – Morphologie, Deformation und Bruchmechanismen von polymeren Werkstoffen. Carl Hanser Verlag, München Wien (1992) ISBN 3-446-170685 (siehe [[AMK-Büchersammlung]] unter F 4) | ||
|-valign="top" | |-valign="top" | ||
|[2] | |[2] | ||
| Zeile 73: | Zeile 76: | ||
|-valign="top" | |-valign="top" | ||
|[3] | |[3] | ||
|Sanadi, A.R., Prasad, S.V. and Rohatgi, P.K.: Sunhemp | |Sanadi, A. R., Prasad, S. V. and Rohatgi, P. K.: Sunhemp Fiber-reinforced Polyester. 1. Analysis of Tensile and Impact Properties. J. Material Science 21 (1986)12, 4299–4304 | ||
|-valign="top" | |-valign="top" | ||
|[4] | |[4] | ||
|Grellmann, W., Bohse, J., Seidler, S.: Bruchmechanische Analyse des Zähigkeitsverhaltens von teilchengefüllten Thermoplasten. Materialw. und Werkstofftechn. 21 (1990) 9, S. 359–364 | |Grellmann, W., Bohse, J., [[Seidler,_Sabine|Seidler, S.]]: Bruchmechanische Analyse des Zähigkeitsverhaltens von teilchengefüllten Thermoplasten. Materialw. und Werkstofftechn. 21 (1990) 9, S. 359–364 | ||
|-valign="top" | |-valign="top" | ||
|[5] | |[5] | ||
|Bohse, J., Grellmann, W., Seidler, S.: Micromechanical | |Bohse, J., Grellmann, W., [[Seidler,_Sabine|Seidler, S]].: Micromechanical Interpretation of Fracture Toughness of Particulate-filled Thermoplastics. J. Material Science 26 (1991) 24, 6715–6721 | ||
|-valign="top" | |-valign="top" | ||
|[6] | |[6] | ||
|Lauke, B., Friedrich, K.: Fracture | |Lauke, B., Friedrich, K.: Fracture Toughness Modelling of Fibre Reinforced Composites by Crack Resistance Curves. Adv. Compos. Mater. 26 (1991) 261–275 | ||
|} | |} | ||
[[Kategorie:Schadensanalyse]] | [[Kategorie:Schadensanalyse]] | ||
Version vom 14. August 2017, 08:50 Uhr
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Bruchverhalten, Kunststoffe
Allgemeines
Polymere Werkstoffe zeigen je nach Typ und Beanspruchungsbedingungen ein sehr unterschiedliches Verhalten beim Bruch.
Einige teilkristalline Polymere wie Polyamid (Kurzzeichen: PA), Polyethylen (Kurzzeichen: PE) und Polypropylen (Kurzzeichen: PP) können bis zu einem Dehnungsverhältnis von = 20 kaltgezogen werden, wobei sich eine stabile Einschnürung entlang des Prüfkörpers bewegt.
Viele amorphe Kunststoffe (z. B. Polystyrol (Kurzzeichen: PS) oder Polymethylmethacrylat (Kurzzeichen: PMMA) sind bei Zugbeanspruchung spröd, verformen sich aber bei Druckspannungen oder reiner Scherbeanspruchung plastisch. Ebenso zeigen Epoxidharze (Kurzzeichen: EP) in Kompression einen hohen Grad an Duktilität. Typische Vertreter eines duktilen und zähen Bruchverhaltens sind z. B. PP, PE oder auch PA.
Typische Mechanismen der plastischen Deformation
Die plastische Deformation tritt bei duktilen Polymeren in zwei Formen auf:
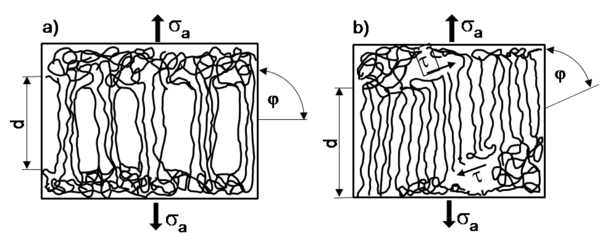
Die Scherdeformation (shear yielding), d. h. die Schubspannungsfließzonenbildung, die eine starke Formänderung ohne Volumenänderung hervorruft. Scherdeformationen zeigen viele teilkristalline Polymere bei Zugbeanspruchung, Raumtemperatur (RT) und Prüfung an Luft (Bild) (siehe: Scherbandbildung).
Das Crazing (Normalspannungsfließzonenbildung), d. h. der Bildung von Hohlräumen. Dieser Prozess verursacht eine starke Dichteänderung und tritt bei Blends und praktisch allen glasartigen Polymeren auf. Bei geringen Beanspruchungen findet man häufig einzelne isolierte Crazes (Bild).
| Bild: | Schematische Darstellung von Deformationserscheinung in amorphen Kunststoffen
(a) Crazes (siehe: Crazing) |
Das Auftreten eines oder beider Mechanismen hängt von folgenden Bedingungen ab:
- Struktur des Makromoleküls
- Kristallisationsgrade und Sphärolithgröße (siehe: Sphärolithische Struktur)
- Deformationsgrad
- Vorhandensein einer zweiten Phase sowie der Testbedingungen
- Temperatur
- Verformungsgeschwindigkeit (siehe auch: Dehnrate Grundlagen)
- dreiachsiger Spannungszustand
- Umgebungsbedingungen
Bruchverhalten, Kurzfaserverbunde
Einsatz und Anwendungsgrenzen von kurzfaserverstärkten Verbundwerkstoffen sind von der Forderung nach möglichst präziser Vorausbestimmung der zu erwartenden Verbundeigenschaft mitbestimmt. Die Vielfalt der Einflussfaktoren lässt eine umfassende Theorie der Mechanik polymerer Verbundwerkstoffe auch künftig nicht zu. Es erscheint daher am zweckmäßigsten, empirisch ermittelte Gesetzmäßigkeiten durch anwendungsgerechte, zielgerichtete Modelle in mathematisch einfachen Formen zu beschreiben.
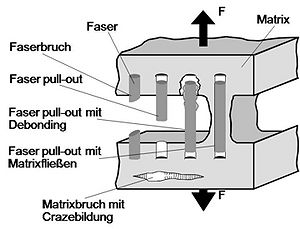
In der Literatur gibt es zahlreiche Bestrebungen, das Zähigkeitsverhalten von faserverstärkten Verbundwerkstoffen durch Modelle zu beschreiben [2, 3]. Wesentliche Grundannahme in diesen Modellen ist oft ein sprödes Werkstoffverhalten. Darauf aufbauend erfolgte die Modellierung des Zähigkeitsverhaltens über theoretische Konzepte, wobei Wechselwirkungsparameter häufig nicht berücksichtigt werden konnten. Allgemein ist der Versagensprozess von kurzfaserverstärkten Kunststoffen jedoch durch das Auftreten energiedissipativer Prozesse gekennzeichnet, wobei die im Bild dargestellten Mechanismen auftreten:
- Faserbruch
- Riss umläuft Faser
- pull-out
- debonding
- plastische Deformation und Matrixversagen
Bruchverhalten, Teilchenverbunde
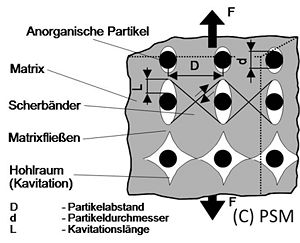
Eine Möglichkeit zur Modellierung der Brucharbeit, die bei instabiler Rissausbreitung und elastisch-plastischem Werkstoffverhalten in teilchengefüllten Thermoplasten verrichtet wird, zeigt das Modell von Bohse [4, 5].
In Analogie zu den Modellvorstellungen von Friedrich und Lauke [6] für Kurzfaserverbunde treten folgende Arbeitsanteile auf:
- Matrix/Teilchen-Ablösung
- nicht lineare viskoelastische Matrixdeformation
- plastische Deformation von Matrixfibrillen
- Fibrillenbruch
Literaturhinweise
| [1] | Michler, G. H.: Kunststoff-Mikromechanik – Morphologie, Deformation und Bruchmechanismen von polymeren Werkstoffen. Carl Hanser Verlag, München Wien (1992) ISBN 3-446-170685 (siehe AMK-Büchersammlung unter F 4) |
| [2] | Friedrich, K. (Ed.): Application of Fracture Mechanics to Composite Materials. Elsevier (Composite Materials Science Volume 6), Amsterdam New York (1989) |
| [3] | Sanadi, A. R., Prasad, S. V. and Rohatgi, P. K.: Sunhemp Fiber-reinforced Polyester. 1. Analysis of Tensile and Impact Properties. J. Material Science 21 (1986)12, 4299–4304 |
| [4] | Grellmann, W., Bohse, J., Seidler, S.: Bruchmechanische Analyse des Zähigkeitsverhaltens von teilchengefüllten Thermoplasten. Materialw. und Werkstofftechn. 21 (1990) 9, S. 359–364 |
| [5] | Bohse, J., Grellmann, W., Seidler, S.: Micromechanical Interpretation of Fracture Toughness of Particulate-filled Thermoplastics. J. Material Science 26 (1991) 24, 6715–6721 |
| [6] | Lauke, B., Friedrich, K.: Fracture Toughness Modelling of Fibre Reinforced Composites by Crack Resistance Curves. Adv. Compos. Mater. 26 (1991) 261–275 |