Einachsiger Spannungszustand: Unterschied zwischen den Versionen
| Zeile 103: | Zeile 103: | ||
|-valign="top" | |-valign="top" | ||
|[1] | |[1] | ||
|Lüpke, T.: Grundlagen mechanischen Verhaltens. In: [[Grellmann,_Wolfgang|Grellmann, W.]], [[Seidler,_Sabine|Seidler, S.]] (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024) 4. Auflage | |Lüpke, T.: Grundlagen mechanischen Verhaltens. In: [[Grellmann,_Wolfgang|Grellmann, W.]], [[Seidler,_Sabine|Seidler, S.]] (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024), 4. Auflage S. 75–91 (ISBN 978-3-446-44718-9; E-Book: ISBN 978-3-446-48105-3; siehe [[AMK-Büchersammlung]] unter A 23) | ||
|-valign="top" | |-valign="top" | ||
|[2] | |[2] | ||
Aktuelle Version vom 9. Oktober 2024, 08:55 Uhr
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Einachsiger Spannungszustand
Spannungszustand im Zug- und Druckversuch
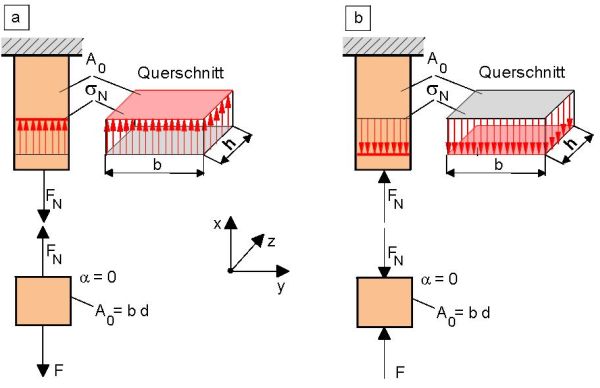
Wird ein Prüfkörper, der sich voraussetzungsgemäß im ebenen Spannungszustand befinden soll durch eine Zug- oder Druckkraft belastet (Bild 1), dann entsteht entsprechend den Schnittreaktionen mit dem Schnittwinkel = 0 im Prüfkörper eine der äußeren Belastung F entsprechende Normalkraft FN. Bei Freiheit von inneren oder äußeren Inhomogenitäten wie Lunkern, Einschlüssen oder Kerben sowie Entformungsneigungen verteilt sich die eingeprägte Belastung als Flächenlast über dem Prüfkörperquerschnitt A0 und wird als normierte Kraft oder Normalspannung entsprechend Gl. (1) angegeben. Diese Normalspannung x oder N besitzt im Fall der Zugbeanspruchung ein positives und bei Druck ein negatives Vorzeichen und ist unter den genannten Voraussetzungen im Prüfkörperquerschnitt konstant [1, 2].
| Bild 1: | Einachsiger Spannungszustand im Zugversuch (a) und im Druckversuch (b) |
| (1) |
Der MOHR'sche Spannungskreis
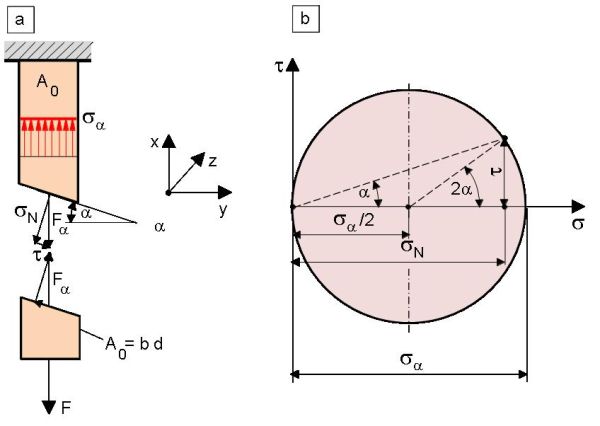
Werden die Schnittreaktionen unter einem Winkel > 0 ermittelt, dann erhält man ein Kräfteparallelogramm der Reaktionskräfte (Bild 2a) und aus den Gleichgewichtsbedingungen ergeben sich nach den Gln. (2) und (3) die im Prüfkörperquerschnitt wirkende Normalspannung N und die Schubspannung [3].
| (2) | ||
| (3) |
| Bild 2: | Schnittreaktionen unter dem Winkel (a) und Mohrscher Spannungskreis (b) |
Aus den Gln. (2) und (3) erhält man die Gl. (4) des MOHR'schen Spannungskreises (benannt nach Christian Otto Mohr), indem die zu dem Schnittwinkel zugehörigen Normal- und Schubspannungen dargestellt sind [3].
| (4) |
Aus der Darstellung in Bild 2b wird ersichtlich, dass das Maximum der Schubspannung unter einem Winkel = 45 ° auftritt und damit τmax= σα/2 beträgt. Makroskopisch äußert sich die Schubspannungskomponente im Zug- oder Druckversuch z. B. durch den Gleit- oder Schiebungsbruch sowie Verformungskegel bei duktilen Metallen als auch durch die auf der Oberfläche sichtbaren Fließlinien, die auch als Lüderslinien bezeichnet werden. Bei Kunststoffen können im Zugversuch unter bestimmten Prüfbedingungen auf der Prüfkörperoberfläche sogenannte Scherbänder beobachtet werden, die einen der dominanten Verformungsprozesse darstellen (Bild 3). Bei duktilen sich einschnürenden Kunststoffen weisen die Flanken der Einschnürfronten oftmals einen näherungsweise unter 45 ° liegenden Winkel auf.
| Bild 3: | Scherbänder bei Acrylnitril-Butadien-Styrol (Kurzzeichen: ABS) im Zugversuch |
Spannungsverteilung bei Dreipunktbiegung
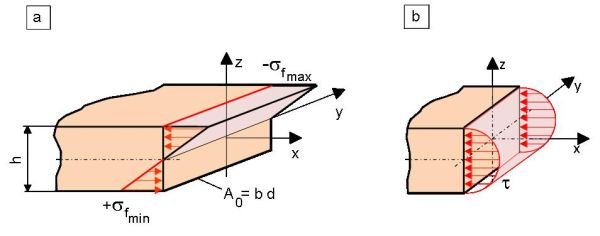
Ein spezieller Fall des einachsigen Spannungszustandes liegt im Fall der reinen Biegung um eine Achse vor, wobei infolge des gleichzeitigen Auftretens von Zug-, Druck- und Schubspannungen hier jedoch ein inhomogener Spannungszustand auftritt [2, 4]. Im Fall von identischen Zug- und Druckeigenschaften des untersuchten Werkstoffes wird die maximale Spannung f in der Randfaser des Prüfkörpers bei Dreipunktbiegung nach Gl. (5) berechnet und die Spannungsverteilung im Querschnitt ist symmetrisch mit der neutralen oder spannungs- und dehnungslosen Achse (Bild 4a).
| (5) |
Aufgrund der Querkraftbiegung treten im Querschnitt zusätzlich Schubspannungen auf, die parabolisch verteilt sind und deren Maximum in der neutralen Faser oder Achse liegt (Bild 4b). Diese Schubspannungen sind beim Biegeversuch an Kunststoffen vernachlässigbar, wenn die Bedingung Stützweite L /Prüfkörperdicke h ≥ 16 erfüllt wird.
Vereinfacht lässt sich das Maximum der Schubspannung nach Gl. (6) für einen rechteckigen Querschnitt berechnen [3]:
| (6) |
| Bild 4: | Normalspannungsverteilung (a) und Verteilung der Schubspannung (b) im Querschnitt eines Prüfkörpers bei Dreipunktbiegung |
Infolge der Querkraftschubempfindlichkeit von Laminaten oder schichtartig aufgebauten Werkstoffverbunden und der möglichen Gefahr von auftretenden Delaminationen muss bei diesen Werkstoffen im Biegeversuch die Bedingung L/h ≥ (20−25) erfüllt werden. Bei differierendem Zug- und Druckverhalten des Werkstoffes tritt eine Verschiebung der neutralen Faser auf, wodurch die Spannungsverteilung im Querschnitt nichtlinear und asymmetrisch ist.
Siehe auch
Literaturhinweise
| [1] | Lüpke, T.: Grundlagen mechanischen Verhaltens. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024), 4. Auflage S. 75–91 (ISBN 978-3-446-44718-9; E-Book: ISBN 978-3-446-48105-3; siehe AMK-Büchersammlung unter A 23) |
| [2] | Bierögel, C.: Quasistatische Prüfverfahren. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024), 4. Auflage S. 106–151 (ISBN 978-3-446-44718-9; E-Book: ISBN 978-3-446-48105-3; siehe AMK-Büchersammlung unter A 23) |
| [3] | Szabo, I.: Einführung in die Technische Mechanik. Springer Verlag, Berlin Heidelberg (1984) 8. Auflage (ISBN 3-540-13293-7) |
| [4] | Erhard, G.: Konstruieren mit Kunststoffen. Carl Hanser Verlag, München (2008) 7. Auflage, S. 189–198 (ISBN 978-3-446-41646-8) |