Auswertemethode nach Sumpter und Turner

Auswertemethode nach Sumpter und Turner

J-Integral-Auswertungsmethode

Bei der Bestimmung von bruchmechanischen Kennwerten nach dem J-Integral-Konzept werden J-Integral-Methoden eingesetzt.

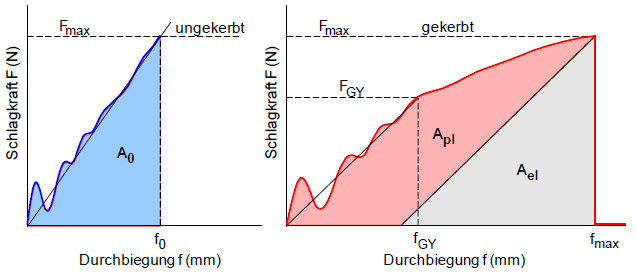
Von SUMPTER und TURNER [1] stammt der Vorschlag zur Bestimmung von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle J_{I}^{ST}} -Werten, die gesamte, von der äußeren Kraft eingebrachte, Energie A_G in zwei Anteile aufzuspalten, also einen elastischen A_el und einen plastischen A_pl Anteil mit:

A_G = A_el + A_pl

Bild 1:

Bestimmung des J-Integrals nach SUMPTER und TURNER [1, 2]

Die Bestimmung von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle J_{I}^{ST}} -Werten ist dann durch folgende Gleichung gegeben:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle J_{I}^{ST}=\eta_{el}\frac{A_{el}}{B(W-a)}+\eta_{pl}\frac{A_{pl}}{B(W-a)}\cdot (\frac{W-a_{eff}}{W-a})}

gültig für 0 < a/W < 1

f(a/W) = 2 für a/w > 0,45

mit

Ael		elastischer Anteil an der Verformungsenergie
Apl		plastischer Anteil an der Verformungsenergie
ηel		elastischer Faktor
ηpl		plastischer Faktor und
ηel, ηpl		= f(a/W)

η_el kann aus dem elastischen Teil der Kraft-Kraftangriffspunktverschiebung-Kurve bestimmt werden

η_pl ist bei Dreipunktbiegeprüfkörpern für a/W > 0,2 η_pl = 2
η_pl ist bei Compact Tension-Prüfkörpern für a/W > 0,6 η_pl = 2 (siehe ASTM STP 700)

Für SENB-Prüfkörper gilt folgende Beziehung für η_el:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \eta_{el}=\frac{2F_{gy}s^2(W-a)}{f_{gy}EBW^3}f^2\left( \frac{a}{W}\right )(1-\nu^2)}

mit: f(a/W) als Korrekturfunktion

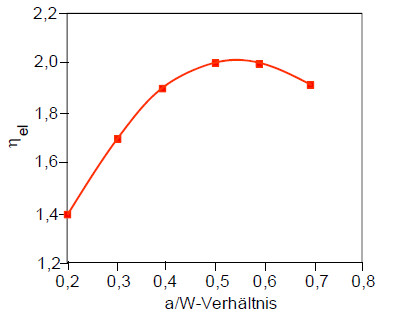
In der Literatur wird von Schwalbe [3] und Blumenauer [4] der folgende Zusammenhang angegeben (Tabelle):

Tabelle: Werte für η_el bei unterschiedlichen Prüfkörpern und a/W-Verhältnissen

ηel	a/W	0,2	0,3	0,4	0,5	0,6	0,7
SENB	s/W = 4	1,4	1,7	1,9	2,0	2,0	1,9
CT	H/W = 1,2	3,7	2,7	2,4	2,3	2,2	2,2

Bild 2:

Zusammenhang zwischen elastischem Faktor und dem a/W-Verhältnis [5, 6]

η_el ist für den SENB-Prüfkörper wie folgt definiert:

η_el = 5(a/W)² + 5,5(a/W) + 0,5

η_pl ist auch über COD-Versuchstechnik ermittelbar, erfordert dann aber Kenntnis über den Rotationsfaktor n:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \eta_{pl}=2-\frac{\left(1-\frac{a}{W}\right)(0,892)-4,476\frac{a}{W}}{1,125+0,892\frac{a}{W}-2,238\left( \frac{a}{W}\right )^2}}

Die experimentelle Vorgehensweise zur Ermittlung von geometrieunabhängigen bruchmechanischen Kennwerten mit Hilfe des instrumentierten Kerbschlagbiegeversuches (IKBV) bei dynamischer Beanspruchung wird in der validierten Prozedur des Prüflabors „Mechanische Prüfung von Kunststoffen“: MPK-Prozedur „MPK-IKBV“ ausführlich erläutert [7].

Literaturhinweise

[1]	Sumpter, J. D. G., Turner, C. E.: ASTM STP 601 (1976): Cracks and Fracture. Method for Laboratory Determination of Jc. p. 3–18
[2]	Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 264/265 und S. 271–273 (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18)
[3]	Schwalbe, K.-H.: Bruchmechanik metallischer Werkstoffe. Carl Hanser Verlag, München Wien (1980), (ISBN: 3-446-12983-9; siehe AMK-Büchersammlung unter E15)
[4]	Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig (1981) 1. Auflage, (siehe AMK-Büchersammlung unter E 29-1)
[5]	Sumpter, J. D. G.: Elastic-Plastic Fracture Analysis and Design Using the Finite Element Method. Ph.D thesis University of London (1974)
[6]	Chipperfield, C. G.: A Summary and Comparison of J Estimation Procedure. Journal of Testing and Evaluation (JTEVA), Vol. 6 No. 4 July (1978) 253–259
[7]	MPK-Prozedur MPK-IKBV (2016-08): Prüfung von Kunststoffen – Instrumentierter Kerbschlagbiegeversuch: Prozedur zur Ermittlung des Risswiderstandverhaltens aus dem instrumentierten Kerbschlagbiegeversuch