Dehnrate Grundlagen

Ein Service der
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung
PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Dehngeschwindigkeit Grundlagen

Dehngeschwindigkeit oder Dehnrate – Grundlagen

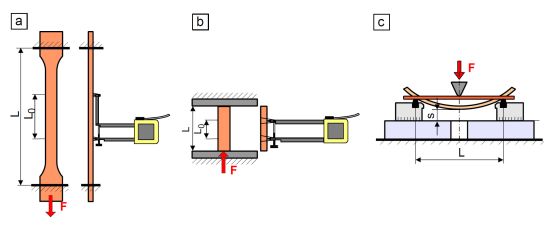
Die Dehngeschwindigkeit dε/dt, auch als Dehnrate bezeichnet, gibt die Geschwindigkeitsverteilung der Dehnung entsprechend der Versuchsart im Volumen des Prüfkörpers infinitesimal oder integral innerhalb einer definierten Prüfkörperlänge an. Bei den Werkstoffprüfungen wird davon ausgegangen, dass sich die eingeprägte Prüfgeschwindigkeit bei quasistatischen Versuchen über das Lastgestänge und die Klemmeinrichtung bzw. die Wider- oder Auflager adäquat in der Prüfkörperquerschnittsfläche und -länge verteilt. Betrachtet man nur den Zug- oder Druckversuch (Bild 1a und b),

Bild 1:

Messung der normativen Dehnung (a) im Zugversuch, (b) im Druckversuch und (c) im Dreipunktbiegeversuch an Kunststoffen

dann kann aus der Traversengeschwindigkeit direkt die nominelle Dehngeschwindigkeit bei Kenntnis der Einspannlänge bzw. dem Druckstempelabstand L mit dε/dt = v_T/L berechnet werden. Da aber der Lasteintrag in den Prüfkörper von dem Steifigkeitsverhältnis zwischen Prüfmaschine und Prüfkörper, der Güte der Einspannklemmen und der Linearität der Lastlinie (Biegeeffekte), der Qualität des Antriebs und der Oberfläche des Prüfkörpers (Rutschen) und dessen Geometrie abhängt, weicht die tatsächliche Dehngeschwindigkeit teilweise erheblich von der berechneten ab. Das kann behoben werden, indem dehnungsgeregelte Zug- oder Druckversuche, die allerdings nicht genormt sind, durchgeführt werden und innerhalb der Messlänge L₀ von Dehnmessfühlern die integrale normative Dehnung und Dehnrate ermittelt wird.

Einfluss der Prüfkörpergeometrie auf die Dehnrate

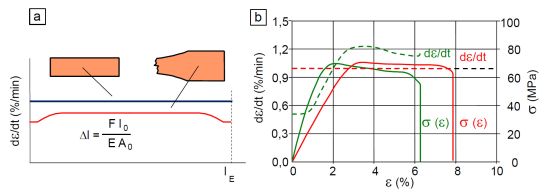
Aus dem Vergleich eines Zugversuchs an prismatischen Prüfkörpern und Vielzweckprüfkörpern mit Schultern zur Einspannung wird ersichtlich, wie sich die Prüfkörpergeometrie auf das Geschwindigkeitsprofil im Prüfkörper auswirkt. In Bild 2a ist zu erkennen, dass sich unter Voraussetzung eines homogenen und isotropen Werkstoffverhalten und Vernachlässigung von Einspanneffekten im prismatischen Prüfkörper eine konstante Verteilung der Dehngeschwindigkeit einstellt (schwarze Kurve in Bild 2a). Bei Anwesenheit von Schultern im oberen und unteren Prüfkörperbereich wird sich aufgrund der veränderten Geometrie A₀ eine geringere mittlere Dehngeschwindigkeit einstellen, die zudem auch nicht konstant ist (rote Kurve in Bild 2a). Wird der Zugversuch bei einer Einspannlänge l_E von 100 mm konventionell mit vergleichbarer konstanter Traversengeschwindigkeit v_T und dehnungsgeregelt durchgeführt, dann ergeben sich die Diagramme entsprechend Bild 2b. Die grünen Kurven in Bild 2b zeigen das Spannungs-Dehnungs-Verhalten (durchgezogene Linie in Bild 2b) und die Dehngeschwindigkeit dε/dt (gestrichelte Linie in Bild 2b) für den konventionellen Zugversuch. Im Vergleich zum dehnungsgeregelten Zugversuch (rote Linien in Bild 2b) liegt eine höhere Zugfestigkeit und geringere Bruchdehnung vor, da im geregelten Versuch verbesserte Relaxationskonditionen für den Kunststoff vorliegen. Wesentlich ist jedoch, dass im geregelten Versuch zwischen den Dehnmessfühlern eine konstante Dehngeschwindigkeit vorliegt, wogegen im konventionellen Zugversuch nur bei ca. 2 % Dehnung eine vergleichbare nominelle und normative Dehngeschwindigkeit existiert. Betrachtet man selbst bei integral geregelten Zugversuch die lokale Dehnungs- und Geschwindigkeitsverteilung innerhalb der Messlänge, dann ergeben sich erhebliche Differenzen, die in der Heterogenität der Prüfkörpermorphologie begründet sind (siehe: Laserextensometrie) und bei der Ermittlung der wahren Dehngeschwindigkeit, speziell bei sich einschnürenden Kunststoffen, zu verstärkten Interpretationsproblemen führen können.

Bild 2:

(a) Schematischer Einfluss der Prüfkörpergeometrie und (b) Auswirkung von konventionellen und dehnungsgeregelten Zugversuchen auf die Dehngeschwindigkeit von Polyamid (Kurzzeichen: PA) mit 20 M.-% GF

Die Dehngeschwindigkeit der Randfaser im Biegeversuch

Ähnliche Probleme existieren bei der Ermittlung der Randfaserdehngeschwindigkeit im Biegeversuch (Bild 1c), wobei hier noch Unterschiede zwischen dem Drei- und Vierpunktbiegeversuch auftreten. Speziell bei starken Unterschieden im Zug- und Druckverhalten von Kunststoffen können sich im Biegeversuch Verschiebungen der neutralen Faser ergeben und verfälschende Messeffekte durch die Traversenwegmessungen einstellen [38].
Aufgrund der schlagartigen Beanspruchung in Anwesenheit von Kerben stellt sich im Schlag- oder Fallversuch ein dreiachsiger Deformationszustand ein, der auch eine inhomogene mehrachsige Verteilung der Dehngeschwindigkeit verursacht. Messungen dieser Geschwindigkeitsverteilungen sind nur an Modellwerkstoffen unter idealisierten Bedingungen mit aufwendigen Versuchstechniken möglich. In den meisten Fällen wird eine theoretische Analyse mittels FEM zur Bewertung der sich einstellenden Dehngeschwindigkeiten in den Belastungsrichtungen herangezogen. Aufgrund der starken Effekte infolge der Spannungsüberhöhung an scharfen Kerben bei den schlagartigen Beanspruchungen wird jedoch eine starke Lokalisierung und Inhomogenität in der Verteilung der Dehngeschwindigkeit hervorgerufen, die sich auf die Zähigkeits­eigenschaften von Kunststoffen sehr stark auswirkt.

Wiki-Begriffserläuterungen zur Geschwindigkeit

Im Rahmen des WIKI-Lexikons Kunststoffprüfung und Diagnostik werden unter Geschwindigkeit auch die nachstehenden Begriffe näher erläutert:

1. siehe Deformationsgeschwindigkeit
2. siehe Verformungsgeschwindigkeit
3. siehe Prüfgeschwindigkeit
4. siehe Dehngeschwindigkeit oder Dehnrate
   - Applikationen
5. siehe Traversengeschwindigkeit

Literaturhinweis

[1]	Bierögel, C.: Quasistatische Prüfverfahren. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 111–157 (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18)