Äquivalentenergiekonzept: Unterschied zwischen den Versionen
| Zeile 11: | Zeile 11: | ||
Verwendet man eine Darstellung in Normkoordinaten (bezogenen Koordinaten), so lässt sich das Verformungsverhalten aller Prüfkörper in einer einzigen Abhängigkeit darstellen. | Verwendet man eine Darstellung in Normkoordinaten (bezogenen Koordinaten), so lässt sich das Verformungsverhalten aller Prüfkörper in einer einzigen Abhängigkeit darstellen. | ||
| − | [[Datei:equiv_bild1.jpg]] | + | [[Datei:equiv_bild1.jpg]]<br> |
Bild 1: Kraft-Kraftangriffspunktverschiebungs-Kurve in bezogenen Koordinaten F/B<sub>2</sub> und v/B für geometrisch ähnliche Prüfkörper A, C und D mit unterschiedlicher Dicke | Bild 1: Kraft-Kraftangriffspunktverschiebungs-Kurve in bezogenen Koordinaten F/B<sub>2</sub> und v/B für geometrisch ähnliche Prüfkörper A, C und D mit unterschiedlicher Dicke | ||
| Zeile 21: | Zeile 21: | ||
=== Voraussetzungen === | === Voraussetzungen === | ||
| − | + | #. A, C und D sind geometrisch ähnliche Prüfkörper<br> | |
| − | + | #. B<sub>D</sub> > B<sub>C</sub> > B<sub>A</sub>; An den Punkten A, C und D erfolgt der Bruch der entsprechenden Prüfkörper<br> | |
| − | + | #. Während der Bruch des Prüfkörpers mit der Dicke BD noch rein elastisch ist, wächst mit abnehmender Dicke das Verhältnis der Energien beim Bruch bezogen auf Probe D an. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Aus der zum Bruch eines kleinen Prüfkörpers mit elastisch-plastischer Verformung notwendigen Energie kann nun auf die Energie, die zum Bruch eines großen Prüfkörpers mit elastischer Verformung notwendig ist, geschlossen werden. Die Fläche unter dieser Kurve hat die Dimension einer auf das Volumen bezogenen Energie, weshalb sie daher auch als volumetrische Energie bezeichnet wird. Aus diesem Grund könnte man diese Aussage auch auf die volumetrische Energie beziehen. Die experimentelle Bestimmung des K-Faktors erfolgt über die Ermittlung einer pseudoelastischen Kraft <math>F^*_Q</math>. | ||
| + | [[Datei:equiv_bild2.jpg]]<br> | ||
| + | Bild 2: Bestimmung der pseudoelastischen Kraft <math>F^*_Q</math> nach dem Äquivalentenergiekonzept | ||
| + | Zunächst wird der Flächeninhalt A<sub>1</sub> unter der Kraft-Kraftangriffspunktverschiebungs-Kurve – im Falle des instrumentierten Kerbschlagbiegeversuches wäre dies die Schlagkraft-Durchbiegungs-Kurve – bestimmt. Dann wird durch Anlegen der Tangente an die Kraft-Kraftangriffspunktverschiebungs-Kurve unter Berücksichtigung der Flächengleichheit A<sub>1</sub> ≡ A<sub>2</sub> die pseudoelastische Kraft nach der Gleichung | ||
| + | <math>F^*_Q = \sqrt{2 A_1 tan\,\alpha}</math> | ||
berechnet. Entsprechend Bild 2 ist tan α der Anstieg der Kraft-Kraftangriffspunkt-verschiebungs-Kurve bei CT- und SENT-Prüfkörpern bzw. der Kraft-Durchbiegungs-Kurven bei Dreipunktbiegeprüfkörpern. | berechnet. Entsprechend Bild 2 ist tan α der Anstieg der Kraft-Kraftangriffspunkt-verschiebungs-Kurve bei CT- und SENT-Prüfkörpern bzw. der Kraft-Durchbiegungs-Kurven bei Dreipunktbiegeprüfkörpern. | ||
| Zeile 47: | Zeile 38: | ||
Für die Gleichung der Spannungsintensitätsfaktoren für die einzelnen Prüfkörper erhält man unter Vernachlässigung der Herleitung: | Für die Gleichung der Spannungsintensitätsfaktoren für die einzelnen Prüfkörper erhält man unter Vernachlässigung der Herleitung: | ||
| − | A. Dreipunktbiegeprüfkörper (SENB – Single Edge Notch Bend) | + | ==== A. Dreipunktbiegeprüfkörper (SENB – Single Edge Notch Bend) ==== |
| + | <math>K^E_I=\frac{F^*_Q \, \cdot\,s} {B \, \cdot\, W^{3/2}}f\left(\frac{a_{eff}}{W}\right)</math> | ||
| − | + | mit <math>f\left(\frac{a}{W}\right)\, = \,2,9\,\frac{a}{W}^{1/2} – 4,6\,\frac{a}{W}^{3/2} \,+ \,21,8\frac{a}{W}^{5/2}\,– \,37,6 \frac{a}{W}^{7/2} \,+ \,38,7\frac{a}{W}^{9/2} | |
| − | |||
| − | mit f(a | ||
| − | und a = | + | und <math>a\, =\, a_{eff}</math> |
| − | |||
| − | |||
| − | |||
| − | |||
| + | ==== B. Kompaktzugprüfkörper (CT-Prüfkörper – Compact Tension)==== | ||
| − | + | <math>K^E_I=\frac{F^*_Q}{B \, \cdot\, W^{1/2}}f\left(\frac{a_{eff}}{W}\right)</math> | |
| − | + | mit <math>f\left(\frac{a}{W}\right)\, = \,29,6\,\frac{a}{W}^{1/2}\,–\, 1855\frac{a}{W}^{3/2}\,+ \,655,7\frac{a}{W}^{5/2}\,– \,1017\frac{a}{W}^{7/2}\,+\, 638,9\frac{a}{W}^{9/2}</math> | |
| − | und a = | + | und <math>a\, =\, a_{eff}</math> |
| − | C. Einseitig gekerbter Zugprüfkörper (SENT-Prüfkörper (Single Edge Notched Tension) | + | ==== C. Einseitig gekerbter Zugprüfkörper (SENT-Prüfkörper (Single Edge Notched Tension)==== |
| − | + | <math>K^E_I=\frac{F^*_Q \, \cdot\,a^{1/2}} {B \, \cdot\, W}f\left(\frac{a_{eff}}{W}\right)</math> | |
| − | mit f(a | + | mit <math>f\left(\frac{a}{W}\right)\, = \,1,99\,–\, 0,41\frac{a}{W}\,+\, 18,7\frac{a}{W}^{2}\,–\, 38,48\frac{a}{W}^{3}\,+ \,53,85\frac{a}{W}^{4}\, |
| − | und a = | + | und <math>a\, =\, a_{eff}</math> |
Die Überprüfung der Geometrieunabhängigkeit erfolgt über die Beziehungen | Die Überprüfung der Geometrieunabhängigkeit erfolgt über die Beziehungen | ||
| Zeile 83: | Zeile 70: | ||
mit β1 = 15 …..125 [5,6], die auch als Geometriekriterium oder vereinfachend als Dickenkriterium bezeichnet werden. | mit β1 = 15 …..125 [5,6], die auch als Geometriekriterium oder vereinfachend als Dickenkriterium bezeichnet werden. | ||
| − | Literaturhinweise | + | '''Literaturhinweise''' |
| − | + | <ul><li>1. Witt, F.J., Mager, T. R.: Nucl. Eng. Des. 17 (1971) S. 91</li> | |
| − | + | <li>2. Witt, F.J.: Nucl. Eng. Des. 20 (1972) S. 237</li> | |
| − | + | <li>3. Grellmann, W.: In: Schmiedel, H. (Hrsg.): Handbuch der Kunststoffprüfung. Carl Hanser Verlag München Wien (1992) S. 145/146 und 175</li> | |
| − | + | <li>4. Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag München Wien (2005) | |
| − | + | <li>5. Eigene Ergebnisse, unveröffentlicht</li> | |
| − | + | <li>6. Grellmann, W., Che, M.: Assessment of Temperature-Dependent Fracture Behaviour with Different Fracture Mechanic Concepts on Example of Unoriented and Cold-Rolled Polypropylene. J. Appl. Polym. Sci. 66 (1997) pp. 1237-1249</li></ul> | |
Version vom 18. Juli 2010, 14:15 Uhr
Äquivalentenergiekonzept
Grundlagen
Das Äquivalentenergiekonzept von Witt und Mager [1,2] ist hinsichtlich seiner Aussagemöglichkeiten in die linear-elastischen Methoden der Bruchmechanik einzuordnen [3]. Die Entwicklung und Anwendung des J-Integral-Konzeptes hat die Äquivalentenergiemethode in den Hintergrund treten lassen, so dass sie zumeist in neueren Büchern [4] auch nicht mehr erwähnt wird.
Das von Witt und Mager auf der Grundlage eines Energievergleiches im elastisch-plastischen Spannungszustand entwickelte Konzept geht von der Untersuchung des Verformungsverhaltens von geometrisch ähnlichen, aber unterschiedlich dicken Prüfkörpern mit Rissen aus.
An diesen Prüfkörpern werden Kraft-Kraftangriffspunktverschiebungs-Kurven aufgenommen und die zum Bruch der Prüfkörper benötigten Kräfte F und die dabei auftretenden Durchbiegungen f bzw. allgemeinen Verschiebungen v werden registriert und in einem Diagramm gegeneinander aufgetragen.
Verwendet man eine Darstellung in Normkoordinaten (bezogenen Koordinaten), so lässt sich das Verformungsverhalten aller Prüfkörper in einer einzigen Abhängigkeit darstellen.
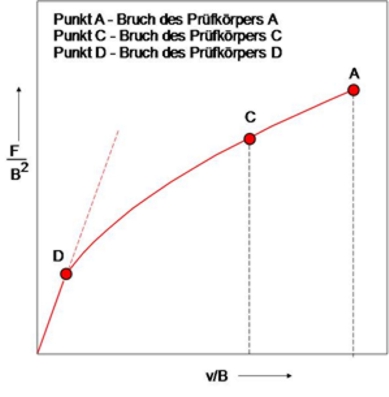
Bild 1: Kraft-Kraftangriffspunktverschiebungs-Kurve in bezogenen Koordinaten F/B2 und v/B für geometrisch ähnliche Prüfkörper A, C und D mit unterschiedlicher Dicke
Grundannahme
Das Verhältnis der volumenbezogenen Bruchenergie ist gleich dem reziproken Verhältnis der Dickenabhängigkeit.
Voraussetzungen
- . A, C und D sind geometrisch ähnliche Prüfkörper
- . BD > BC > BA; An den Punkten A, C und D erfolgt der Bruch der entsprechenden Prüfkörper
- . Während der Bruch des Prüfkörpers mit der Dicke BD noch rein elastisch ist, wächst mit abnehmender Dicke das Verhältnis der Energien beim Bruch bezogen auf Probe D an.
Aus der zum Bruch eines kleinen Prüfkörpers mit elastisch-plastischer Verformung notwendigen Energie kann nun auf die Energie, die zum Bruch eines großen Prüfkörpers mit elastischer Verformung notwendig ist, geschlossen werden. Die Fläche unter dieser Kurve hat die Dimension einer auf das Volumen bezogenen Energie, weshalb sie daher auch als volumetrische Energie bezeichnet wird. Aus diesem Grund könnte man diese Aussage auch auf die volumetrische Energie beziehen. Die experimentelle Bestimmung des K-Faktors erfolgt über die Ermittlung einer pseudoelastischen Kraft .
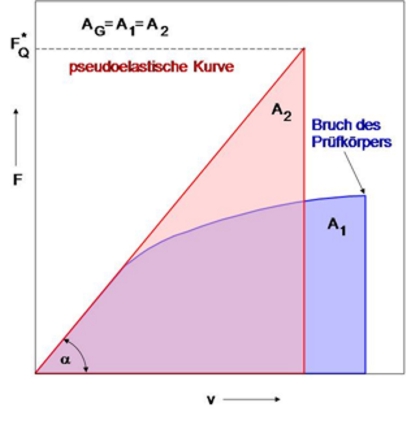
Bild 2: Bestimmung der pseudoelastischen Kraft nach dem Äquivalentenergiekonzept
Zunächst wird der Flächeninhalt A1 unter der Kraft-Kraftangriffspunktverschiebungs-Kurve – im Falle des instrumentierten Kerbschlagbiegeversuches wäre dies die Schlagkraft-Durchbiegungs-Kurve – bestimmt. Dann wird durch Anlegen der Tangente an die Kraft-Kraftangriffspunktverschiebungs-Kurve unter Berücksichtigung der Flächengleichheit A1 ≡ A2 die pseudoelastische Kraft nach der Gleichung
berechnet. Entsprechend Bild 2 ist tan α der Anstieg der Kraft-Kraftangriffspunkt-verschiebungs-Kurve bei CT- und SENT-Prüfkörpern bzw. der Kraft-Durchbiegungs-Kurven bei Dreipunktbiegeprüfkörpern.
Für die Gleichung der Spannungsintensitätsfaktoren für die einzelnen Prüfkörper erhält man unter Vernachlässigung der Herleitung:
A. Dreipunktbiegeprüfkörper (SENB – Single Edge Notch Bend)
mit Fehler beim Parsen (Syntaxfehler): {\displaystyle f\left(\frac{a}{W}\right)\, = \,2,9\,\frac{a}{W}^{1/2} – 4,6\,\frac{a}{W}^{3/2} \,+ \,21,8\frac{a}{W}^{5/2}\,– \,37,6 \frac{a}{W}^{7/2} \,+ \,38,7\frac{a}{W}^{9/2} und <math>a\, =\, a_{eff}}
B. Kompaktzugprüfkörper (CT-Prüfkörper – Compact Tension)
mit Fehler beim Parsen (Syntaxfehler): {\displaystyle f\left(\frac{a}{W}\right)\, = \,29,6\,\frac{a}{W}^{1/2}\,–\, 1855\frac{a}{W}^{3/2}\,+ \,655,7\frac{a}{W}^{5/2}\,– \,1017\frac{a}{W}^{7/2}\,+\, 638,9\frac{a}{W}^{9/2}}
und
C. Einseitig gekerbter Zugprüfkörper (SENT-Prüfkörper (Single Edge Notched Tension)
mit Fehler beim Parsen (Syntaxfehler): {\displaystyle f\left(\frac{a}{W}\right)\, = \,1,99\,–\, 0,41\frac{a}{W}\,+\, 18,7\frac{a}{W}^{2}\,–\, 38,48\frac{a}{W}^{3}\,+ \,53,85\frac{a}{W}^{4}\, und <math>a\, =\, a_{eff}}
Die Überprüfung der Geometrieunabhängigkeit erfolgt über die Beziehungen
mit β als werkstoffabhängige Konstante: 0,6 …. 8,3 [5] bzw.
mit β1 = 15 …..125 [5,6], die auch als Geometriekriterium oder vereinfachend als Dickenkriterium bezeichnet werden.
Literaturhinweise
- 1. Witt, F.J., Mager, T. R.: Nucl. Eng. Des. 17 (1971) S. 91
- 2. Witt, F.J.: Nucl. Eng. Des. 20 (1972) S. 237
- 3. Grellmann, W.: In: Schmiedel, H. (Hrsg.): Handbuch der Kunststoffprüfung. Carl Hanser Verlag München Wien (1992) S. 145/146 und 175
- 4. Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag München Wien (2005)
- 5. Eigene Ergebnisse, unveröffentlicht
- 6. Grellmann, W., Che, M.: Assessment of Temperature-Dependent Fracture Behaviour with Different Fracture Mechanic Concepts on Example of Unoriented and Cold-Rolled Polypropylene. J. Appl. Polym. Sci. 66 (1997) pp. 1237-1249





