Dynamisch-Mechanische Analyse (DMA) – Zugbeanspruchung
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Dynamisch-Mechanische Analyse (DMA) − Zugbeanspruchung
Allgemeines
Bei der dynamisch-mechanischen Analyse unter Zugbeanspruchung wird der verwendete Prüfkörper einer periodisch wechselnden Beanspruchung ausgesetzt, wobei durch die Variation der Frequenz der erzwungenen Schwingung die Charakterisierung der Zeitabhängigkeit des Werkstoffverhaltens möglich ist (DMA). Wird zusätzlich eine Temperierkammer an das Messsystem appliziert, dann kann bei einer konstanten Frequenz auch die Temperaturabhängigkeit der betreffenden Kunststoffe erfasst und dargestellt werden (DMTA).
Durchführung der DMA unter Zugbeanspruchung
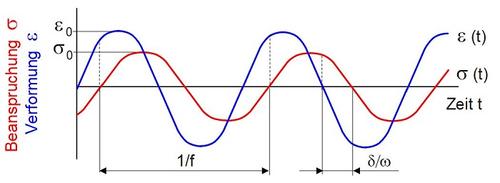
Die DMA bzw. die DMTA unter Zugbeanspruchung zählt zu den dynamisch-mechanischen Prüfverfahren mit erzwungenen Schwingungen, welches für die Charakterisierung viskoelastischer Eigenschaften und der Glastemperatur eingesetzt wird. Dazu wird der Prüfkörper einer sinusförmig wechselnden mechanischen Beanspruchung konstanter Frequenz und konstanter Amplitude ausgesetzt. Bei linear-viskoelastischem Materialverhalten weisen die zeitlichen Änderungen von Spannung und Dehnung im eingeschwungenen Zustand die identische Frequenz, aber unterschiedliche Phasenlagen nach den Gln. (1) und (2) auf (Bild 1).
| Bild 1: | Zeitliche Änderung von Spannung und Dehnung bei dynamisch-mechanischer Analyse unter Verwendung erzwungener Schwingungen |
| (1) |
| (2) |
Infolge der Phasenverschiebung δ zwischen Beanspruchung (Spannung) und der Verformung (Dehnung oder Scherung) ist zur Beschreibung des Spannungs-Dehnungs-Zusammenhanges der Modul als komplexe Größe E* nach der Gl. (3) gültig.
| (3) |
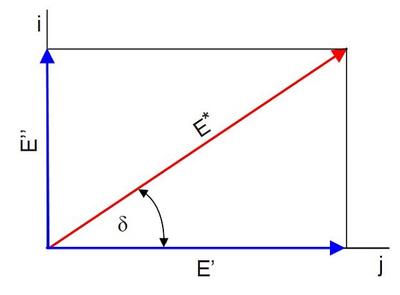
Der komplexe Modul kann als Vektor in der komplexen Zahlenebene betrachtet werden (Bild 2), dessen Richtung durch den Phasenwinkel δ und dessen Betrag durch das Verhältnis der Amplitudenwerte von applizierter erzwungenen Spannung und Dehnung gegeben ist.
| Bild 2: | Darstellung des Moduls E* in der komplexen Zahlenebene |
Der Absolutbetrag des jeweiligen Moduls ergibt sich aus dem Verhältnis der Initialbeanspruchung zur Ausgangsverformung nach der Gl. (4).
| (4) |
Unter Verwendung einfacher trigonometrischer Beziehungen erfolgt dann eine Aufteilung in den Realteil E‘ und den Imaginärteil E‘‘, die mit den Gln. (5) und (6) vorgenommen wird. Der Realteil E‘ wird als Speichermodul bezeichnet und ist ein Maß für die während einer Schwingungsperiode gespeicherte reversible Energie Wrev. Der Imaginäranteil E‘‘ erfasst die in der jeweiligen Periode dissipierte Energie Wirrev und wird als Verlustmodul benannt. Aus dem Verhältnis von Verlust- und Speichermodul ergibt sich der Verlustfaktor d = tan δ, welcher das Dämpfungsverhalten des Werkstoffs nach der Gl. (7) beschreibt. Der Wert δ ist dabei der sogenannte Phasenwinkel, der Werte zwischen 0 und π/2 annehmen kann
| (5) |
| (6) |
| (7) |
Das Verfahren der erzwungenen Schwingungen ist auf Frequenzen unterhalb der Resonanzfrequenz des Prüfkörpers beschränkt. Handelsübliche Geräte arbeiten im Bereich von ca. 10-2 Hz bis 102 Hz, wobei als Messgröße die Leistungsaufnahme des Antriebmotors dient. Die Messung kann sowohl dehnungs- als auch spannungsgeregelt erfolgen, was die Bestimmung des komplexen Moduls E* und der komplexen Nachgiebigkeit mit C* = 1 / E* ermöglicht. Diese Geräte gestatten die Ermittlung komplexer Elastizitätsmoduli in einem weiten Steifigkeitsbereich von 10-3 MPa bis 106 MPa. Der größte Nachteil des Verfahrens liegt allerdings in der geringen Empfindlichkeit bei der Messung kleiner Dämpfungen (tan δ < 0,01), also sehr steifer oder hochmoduliger Werkstoffe. Auf Grund ihrer großen Anwendungsbreite besitzen Verfahren mit erzwungenen Schwingungen heute jedoch eine dominierende Rolle bei der dynamisch-mechanischen Analyse polymerer Werkstoffe.
Gerätesysteme zur Durchführung der DMA und DMTA
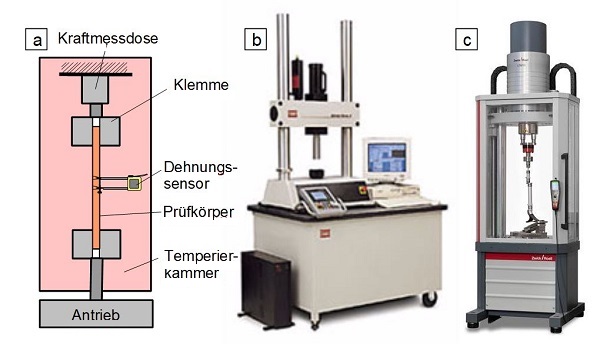
Bei der dynamisch-mechanischen Analyse oder Spektroskopie mittels Zugbeanspruchung können servohydraulische Universalprüfmaschinen für große Kräfte oder Tischprüfsysteme (Stand Alone Systeme) für kleinere Prüfkräfte verwendet werden (Bild 3). Gemeinsam ist allen Verfahren, dass die Deformation des Prüfkörpers sehr klein ist und den linear-viskoelastischen Bereich nicht überschreiten sollte. Infolge dieser kleinen Verformungen sind mit der DMA oder DMTA im Temperaturintervall von ca. –180 °C bis 400 °C hohe Prüffrequenzen bei mechanischer Anregung bis zu 200 Hz realisierbar [1, 2]. Für die Kunststoffprüfung mittels DMA oder DMTA unter Zugbeanspruchung [3] werden zur Erzeugung sinusförmiger Dehnungen oder Spannungen vorwiegend hydraulische, pneumatische oder elektrodynamische Kleinprüfmaschinen, wobei die Versuche kraft- oder dehnungsgeregelt durchgeführt werden können.
| Bild 3: | DMTA-System (a) Schematischer Aufbau, (b) Servohydraulisches System MTS 858, Berlin, und (c) ZWICK LTS 5 kN – System, ZwickRoell GmbH & Co. KG, Ulm |
Bei den Tischprüfsystemen (siehe auch: Lastrahmen) existiert in Abhängigkeit von der Prüfkraft und der Ausstattung ebenfalls eine große Auswahl an kommerziellen Prüfsystemen, wobei diese in der Regel mit Zusatzeinrichtungen wie Dehnungssensoren und Temperierkammern (Bild 4) ausgestattet sind.
| Bild 4: | DMTA-Systeme (a) Mettler Toledo, Greifensee, Schweiz (b) MPAS der Fa. Gabo Qualimeter GmbH, Ahlden |
Von dem Prüfsystem wird dann eine konstante sinusförmige Dehnungs- oder Spannungsamplitude mit einer definierten und konstanten Frequenz auf den Prüfkörper aufgebracht, wobei in der Kunststoffprüfung aufgrund der Prüfkörpergeometrie bevorzugt im Zugschwellbereich gearbeitet wird. Die Amplitude der Spannung oder Dehnung sowie die Mittelspannung oder -dehnung als auch die Temperatur werden per PID-Regelung auf konstantem Niveau gehalten, um Kriech- oder Relaxationseffekte während des Versuchs zu kompensieren.
Siehe auch
- Dynamisch-Mechanische Analyse (DMA) – Grundlagen
- Dynamisch-Mechanische Analyse (DMA) – Torsionsbeanspruchung
- Dynamisch-Mechanische Analyse (DMA) – Biegebeanspruchung
- Elastizitätsmodul
Literaturhinweise
| [1] | Lüpke, T.: Grundlagen mechanischen Verhaltens. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024) 4. Auflage, S. 96–98 (ISBN 978-3-446-44718-9; E-Book: ISBN 978-3-446-48105-3; siehe AMK-Büchersammlung unter A 23) |
| [2] | DIN EN ISO 6721-1 (2019-09): Kunststoffe – Bestimmung dynamisch-mechanischer Eigenschaften – Teil 1: Allgemeine Grundlagen |
| [3] | ISO 6721-4 (2019-05): Kunststoffe – Bestimmung dynamisch-mechanischer Eigenschaften – Teil 4: Zugschwingung – Erzwungene Schwingungen |